22.3 实际问题与二次函数 第3课时课件(共16张PPT)2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 22.3 实际问题与二次函数 第3课时课件(共16张PPT)2023-2024学年人教版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 667.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
22.3 实际问题与二次函数
第3课时
第二十二章 二次函数
1.能根据题意建立适当的平面直角坐标系,利用情境中的条件求二次函数解析式
典型例题
当堂检测
学习目标
课堂总结
2.能利用二次函数的有关知识,解决拱桥相关问题
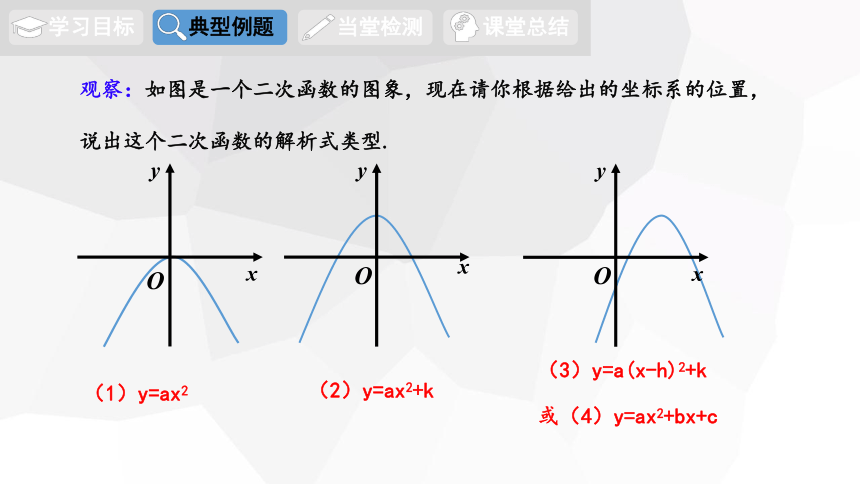
观察:如图是一个二次函数的图象,现在请你根据给出的坐标系的位置,
说出这个二次函数的解析式类型.
x
y
x
y
x
y
O
O
O
(1)y=ax2
(2)y=ax2+k
(3)y=a(x-h)2+k
或(4)y=ax2+bx+c
典型例题
当堂检测
学习目标
课堂总结
例1: 如图,一座拱桥的纵截面是抛物线的一部分,水面宽是4米时,
拱顶离水面2米.求出水面宽3米时,拱顶离水面多少米?
分析:因为纵截面是抛物线的一部分,所以应当
是个二次函数,因此我们可以建立函数模型.
显然以拱顶为原点,抛物线的对称轴为y轴,
建立直角坐标系最为简便.
典型例题
当堂检测
学习目标
课堂总结
解:以拱顶为原点,抛物线的对称轴为y轴,
建立直角坐标系,如图.
由于顶点坐标系是(0,0),因此这个二次函数的形式为y=ax2
已知水面宽4米时,拱顶离水面高2米,因此点A(2,-2)在抛物线上,
由此得出-2=a·22,
解得a=-0.5.
二次函数的为y=-0.5x2.
宽度为3时,x=1.5,这时y=-1.125.
因此水面宽3米时,拱顶离水面1.125米.
典型例题
当堂检测
学习目标
课堂总结
归纳总结
(1)建立合适的平面直角坐标系;
(2)将已知条件转化为点的坐标;
(3)合理地设出所求的函数表达式;
(4)代入已知条件或点的坐标,求出函数表达式;
(5)利用函数表达式解决问题.
解决拱桥问题的一般步骤:
典型例题
当堂检测
学习目标
课堂总结
1.如图所示,某建筑物有一抛物线形的大门,小明想知道这道门的高度,他先测出门的宽度AB=8m,然后用一根长为4m的小竹竿CD竖直的接触地面和门的内壁,并测得AC=2m,则门高OE为_________.
学习目标
典型例题
当堂检测
课堂总结
2.有一座抛物线形拱桥,正常水位时桥下水面宽度为 20m,拱顶距离水面
4 m.如图所示的直角坐标系中,求出这条抛物线表示的函数的解析式;
O
A
B
y
x
20 m
h
解:设该拱桥形成的抛物线的解析式为y=ax2.
∴y=-0.04x2.
∴-4=100a,a=-0.04,
∵该抛物线过(10,-4),
学习目标
典型例题
当堂检测
课堂总结
3.如图一座拱桥的示意图,已知桥洞的拱形是抛物线.当水面宽为12m时,桥洞顶部离水面4m.
(1)建立平面直角坐标系,并求该抛物线的函数表达式;
(2)若水面上升1m,水面宽度将减少多少?
解:以AB的中点为平面直角坐标系的原点O,AB所在线为x轴,过O点作AB的垂线为y轴建立坐标系.
∴62a+4=0
设抛物线为y=ax2+b
x
O
y
∵该抛物线过(6,0),(0,4)
解得:a=
∴抛物线的表达式为y= x2+4.
学习目标
典型例题
当堂检测
课堂总结
3.如图一座拱桥的示意图,已知桥洞的拱形是抛物线.当水面宽为12m时,桥洞顶部离水面4m.
(2)若水面上升1m,水面宽度将减少多少?
解:(2)令y=1
x
O
y
解得:x1= ,x2=
得 x2+4=1
则水面上升1m后的水面宽度为x1-x2= (米)
∴水面上升1m,水面宽度将减少(12- )米.
学习目标
典型例题
当堂检测
课堂总结
例2:如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,
篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离
为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面
3.05m,那么篮球在该运动员出手时的高度是多少米?
典型例题
当堂检测
学习目标
课堂总结
解:如图,建立直角坐标系.
x
y
O
则点A的坐标是(1.5,3.05),篮球在最大高度时的位置为B(0,3.5).
以点C表示运动员投篮球的出手处.
典型例题
当堂检测
学习目标
课堂总结
解得
a=-0.2,
k=3.5,
设以y轴为对称轴的抛物线的解析式为 y=ax2+k.
所以该抛物线的表达式为y=-0.2x2+3.5.
2.25a+k=3.05,
k=3.5,
而点A,B在这条抛物线上,所以有
故该运动员出手时的高度为2.25m.
当x=-2.5时,y=2.25 .
典型例题
当堂检测
学习目标
课堂总结
x
y
O
4.如图,排球运动员站在点O处练习发球,将球从O点正上方2 m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9 m,高度为2.43 m,球场的边界距O点的水平距离为18 m.
(1)当h=2.6时,求y与x的关系式(不要求写出
自变量x的取值范围)
解:(1)∵h=2.6,球从O点正上方2 m的A处发出,
∴y=a(x-6)2+h 过(0,2)点,
∴2=a(0-6)2+2.6,解得:a=
所以y与x的关系式为:y= (x-6)2+2.6
学习目标
典型例题
当堂检测
课堂总结
(2)当h=2.6时,球能否越过球网?会不会出界?请说明理由.
解:(2)
y与x的关系式为:y= (x-6)2+2.6
当x=9时,y= (x-6)2+2.6=2.45>2.43,球能过网,
当y=0时, (x-6)2+2.6=0,
解得:x1=6+ >18,x2=6- (舍去),出界
答:当h=2.6时,球能越过球网,会出界.
学习目标
典型例题
当堂检测
课堂总结
学习目标
典型例题
当堂检测
课堂总结
拱桥问题
运动中的抛物线问题
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
转化的关键
22.3 实际问题与二次函数
第3课时
第二十二章 二次函数
1.能根据题意建立适当的平面直角坐标系,利用情境中的条件求二次函数解析式
典型例题
当堂检测
学习目标
课堂总结
2.能利用二次函数的有关知识,解决拱桥相关问题
观察:如图是一个二次函数的图象,现在请你根据给出的坐标系的位置,
说出这个二次函数的解析式类型.
x
y
x
y
x
y
O
O
O
(1)y=ax2
(2)y=ax2+k
(3)y=a(x-h)2+k
或(4)y=ax2+bx+c
典型例题
当堂检测
学习目标
课堂总结
例1: 如图,一座拱桥的纵截面是抛物线的一部分,水面宽是4米时,
拱顶离水面2米.求出水面宽3米时,拱顶离水面多少米?
分析:因为纵截面是抛物线的一部分,所以应当
是个二次函数,因此我们可以建立函数模型.
显然以拱顶为原点,抛物线的对称轴为y轴,
建立直角坐标系最为简便.
典型例题
当堂检测
学习目标
课堂总结
解:以拱顶为原点,抛物线的对称轴为y轴,
建立直角坐标系,如图.
由于顶点坐标系是(0,0),因此这个二次函数的形式为y=ax2
已知水面宽4米时,拱顶离水面高2米,因此点A(2,-2)在抛物线上,
由此得出-2=a·22,
解得a=-0.5.
二次函数的为y=-0.5x2.
宽度为3时,x=1.5,这时y=-1.125.
因此水面宽3米时,拱顶离水面1.125米.
典型例题
当堂检测
学习目标
课堂总结
归纳总结
(1)建立合适的平面直角坐标系;
(2)将已知条件转化为点的坐标;
(3)合理地设出所求的函数表达式;
(4)代入已知条件或点的坐标,求出函数表达式;
(5)利用函数表达式解决问题.
解决拱桥问题的一般步骤:
典型例题
当堂检测
学习目标
课堂总结
1.如图所示,某建筑物有一抛物线形的大门,小明想知道这道门的高度,他先测出门的宽度AB=8m,然后用一根长为4m的小竹竿CD竖直的接触地面和门的内壁,并测得AC=2m,则门高OE为_________.
学习目标
典型例题
当堂检测
课堂总结
2.有一座抛物线形拱桥,正常水位时桥下水面宽度为 20m,拱顶距离水面
4 m.如图所示的直角坐标系中,求出这条抛物线表示的函数的解析式;
O
A
B
y
x
20 m
h
解:设该拱桥形成的抛物线的解析式为y=ax2.
∴y=-0.04x2.
∴-4=100a,a=-0.04,
∵该抛物线过(10,-4),
学习目标
典型例题
当堂检测
课堂总结
3.如图一座拱桥的示意图,已知桥洞的拱形是抛物线.当水面宽为12m时,桥洞顶部离水面4m.
(1)建立平面直角坐标系,并求该抛物线的函数表达式;
(2)若水面上升1m,水面宽度将减少多少?
解:以AB的中点为平面直角坐标系的原点O,AB所在线为x轴,过O点作AB的垂线为y轴建立坐标系.
∴62a+4=0
设抛物线为y=ax2+b
x
O
y
∵该抛物线过(6,0),(0,4)
解得:a=
∴抛物线的表达式为y= x2+4.
学习目标
典型例题
当堂检测
课堂总结
3.如图一座拱桥的示意图,已知桥洞的拱形是抛物线.当水面宽为12m时,桥洞顶部离水面4m.
(2)若水面上升1m,水面宽度将减少多少?
解:(2)令y=1
x
O
y
解得:x1= ,x2=
得 x2+4=1
则水面上升1m后的水面宽度为x1-x2= (米)
∴水面上升1m,水面宽度将减少(12- )米.
学习目标
典型例题
当堂检测
课堂总结
例2:如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,
篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离
为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面
3.05m,那么篮球在该运动员出手时的高度是多少米?
典型例题
当堂检测
学习目标
课堂总结
解:如图,建立直角坐标系.
x
y
O
则点A的坐标是(1.5,3.05),篮球在最大高度时的位置为B(0,3.5).
以点C表示运动员投篮球的出手处.
典型例题
当堂检测
学习目标
课堂总结
解得
a=-0.2,
k=3.5,
设以y轴为对称轴的抛物线的解析式为 y=ax2+k.
所以该抛物线的表达式为y=-0.2x2+3.5.
2.25a+k=3.05,
k=3.5,
而点A,B在这条抛物线上,所以有
故该运动员出手时的高度为2.25m.
当x=-2.5时,y=2.25 .
典型例题
当堂检测
学习目标
课堂总结
x
y
O
4.如图,排球运动员站在点O处练习发球,将球从O点正上方2 m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9 m,高度为2.43 m,球场的边界距O点的水平距离为18 m.
(1)当h=2.6时,求y与x的关系式(不要求写出
自变量x的取值范围)
解:(1)∵h=2.6,球从O点正上方2 m的A处发出,
∴y=a(x-6)2+h 过(0,2)点,
∴2=a(0-6)2+2.6,解得:a=
所以y与x的关系式为:y= (x-6)2+2.6
学习目标
典型例题
当堂检测
课堂总结
(2)当h=2.6时,球能否越过球网?会不会出界?请说明理由.
解:(2)
y与x的关系式为:y= (x-6)2+2.6
当x=9时,y= (x-6)2+2.6=2.45>2.43,球能过网,
当y=0时, (x-6)2+2.6=0,
解得:x1=6+ >18,x2=6- (舍去),出界
答:当h=2.6时,球能越过球网,会出界.
学习目标
典型例题
当堂检测
课堂总结
学习目标
典型例题
当堂检测
课堂总结
拱桥问题
运动中的抛物线问题
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
转化的关键
同课章节目录
