23.2.3 关于原点对称的点的坐标 课件(共15张PPT) 2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 23.2.3 关于原点对称的点的坐标 课件(共15张PPT) 2023-2024学年人教版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 529.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 23:18:00 | ||
图片预览






文档简介
(共15张PPT)
第二十三章 旋转
23.2.3 关于原点对称的点的坐标
1.掌握两点关于原点对称时,横纵坐标的关系;(重点)
2.会在平面直角坐标系内作关于原点对称的图形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
如图,在直角坐标系中,作出下列
已知点关于原点O的对称点,并写出
它们的坐标.A(4,0),B(0,-3),
C(2,1),D(-1,2),E(-4,-3).
A′(-4,0),B′(0,3),C′(-2,-1),
D′(1,-2),E′(4,3)
A′
B′
C′
D′
E′
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结
关于原点对称的点的坐标的规律:
第一象限内的点关于原点的对称点在第三象限,第二象限内的点关于原点的
对称点在第四象限,坐标轴上的点关于原点的对称点仍在坐标轴上.
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点O的
对称点为P′(-x,-y).
典型例题
当堂检测
学习目标
课堂总结
概念剖析
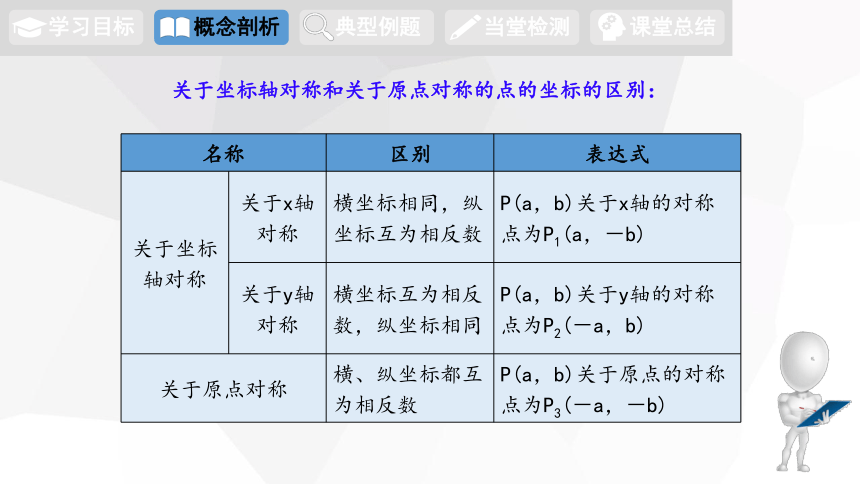
关于坐标轴对称和关于原点对称的点的坐标的区别:
名称 区别 表达式
关于坐标轴对称 关于x轴对称 横坐标相同,纵坐标互为相反数 P(a,b)关于x轴的对称点为P1(a,-b)
关于y轴对称 横坐标互为相反数,纵坐标相同 P(a,b)关于y轴的对称点为P2(-a,b)
关于原点对称 横、纵坐标都互为相反数 P(a,b)关于原点的对称点为P3(-a,-b)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.点A(3,-1)关于原点对称的点A′的坐标是( )
A.(-3,-1) B.(3,1)
C.(-3,1) D.(-1,3)
解析:∵点A(3,-1)与点A′关于原点对称,
∴点A′的坐标是(-3,1).
C
归纳总结
点P(x,y)关于x轴的对称点的坐标为P1(x,-y);
关于y轴的对称点的坐标为P2(-x,y);
关于原点的对称点的坐标为P3(-x,-y).
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.在直角坐标系中,将点(-2,3)关于原点的对称点向左平移2个单位长度
得到的点的坐标是( )
A.(4,-3) B.(-4,3)
C.(0,-3) D.(0,3)
C
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.已知点P(2a+b,-3a)与点P'(8,b+2).
若点P与点P'关于x轴对称,则a=_____ b=_______.
若点P与点P'关于y轴对称,则a=_____ b=_______.
若点P与点P'关于原点对称,则a=_____ b=_______.
4
6
-20
2
-1.2
-5.6
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.若将等腰直角三角形AOB按如图所示放置,OB=2,则点A关于原点对称的点的坐标为________.
(-1,-1)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称
的图形.
-2
2
-2
-4
4
-4
x
y
0
2
4
A
B
C
B
A
C
解:△ABC的三个顶点的坐标
分别为A(-4,1),B(-1,-1),C(-3,2),
依次连接A′,B′,C′便可得到所求作的三角形.
它们关于原点的对称点分别为
A′(4,-1),B′(1,1),C′(3,-2),
归纳总结
作关于原点对称的图形的步骤:
(1)写出各点关于原点对称的点的坐标;
(2)在坐标平面内描出这些对称点;
(3)参照原图形顺次连接各点,即为所求作的对称图形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.已知:如图,E(-4,2),F(-1,-1),以 O 为中心,作 △EFO 的关于
原点中心对称图形.
解:E′的坐标为(4,-2),
F′的坐标为(1,1)
依次连接O,E′,F′,
△E′F′O为△EFO的中心对称图形.
E′
F′
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
5.在如图所示编号为①、②、③、④的四个三角形中,关于y轴对称的两个
三角形的编号为 ;关于坐标原点O对称的两个三角形的编号为 .
y
x
-
1
-
2
-
4
-
3
-
5
-
1
-
2
-
4
-
5
-
3
1
2
4
3
5
1
2
4
3
5
O
①
②
③
④
①与②
①与③
典型例题
当堂检测
学习目标
课堂总结
概念剖析
关于原点对称的点的坐标
1.特征:P(x,y)关于原点的对称点为P'(-x,-y);
2.作图:作出关于原点对称的图形,先求出对称点的坐标再描点画图.
第二十三章 旋转
23.2.3 关于原点对称的点的坐标
1.掌握两点关于原点对称时,横纵坐标的关系;(重点)
2.会在平面直角坐标系内作关于原点对称的图形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
如图,在直角坐标系中,作出下列
已知点关于原点O的对称点,并写出
它们的坐标.A(4,0),B(0,-3),
C(2,1),D(-1,2),E(-4,-3).
A′(-4,0),B′(0,3),C′(-2,-1),
D′(1,-2),E′(4,3)
A′
B′
C′
D′
E′
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结
关于原点对称的点的坐标的规律:
第一象限内的点关于原点的对称点在第三象限,第二象限内的点关于原点的
对称点在第四象限,坐标轴上的点关于原点的对称点仍在坐标轴上.
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点O的
对称点为P′(-x,-y).
典型例题
当堂检测
学习目标
课堂总结
概念剖析
关于坐标轴对称和关于原点对称的点的坐标的区别:
名称 区别 表达式
关于坐标轴对称 关于x轴对称 横坐标相同,纵坐标互为相反数 P(a,b)关于x轴的对称点为P1(a,-b)
关于y轴对称 横坐标互为相反数,纵坐标相同 P(a,b)关于y轴的对称点为P2(-a,b)
关于原点对称 横、纵坐标都互为相反数 P(a,b)关于原点的对称点为P3(-a,-b)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.点A(3,-1)关于原点对称的点A′的坐标是( )
A.(-3,-1) B.(3,1)
C.(-3,1) D.(-1,3)
解析:∵点A(3,-1)与点A′关于原点对称,
∴点A′的坐标是(-3,1).
C
归纳总结
点P(x,y)关于x轴的对称点的坐标为P1(x,-y);
关于y轴的对称点的坐标为P2(-x,y);
关于原点的对称点的坐标为P3(-x,-y).
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.在直角坐标系中,将点(-2,3)关于原点的对称点向左平移2个单位长度
得到的点的坐标是( )
A.(4,-3) B.(-4,3)
C.(0,-3) D.(0,3)
C
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.已知点P(2a+b,-3a)与点P'(8,b+2).
若点P与点P'关于x轴对称,则a=_____ b=_______.
若点P与点P'关于y轴对称,则a=_____ b=_______.
若点P与点P'关于原点对称,则a=_____ b=_______.
4
6
-20
2
-1.2
-5.6
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.若将等腰直角三角形AOB按如图所示放置,OB=2,则点A关于原点对称的点的坐标为________.
(-1,-1)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称
的图形.
-2
2
-2
-4
4
-4
x
y
0
2
4
A
B
C
B
A
C
解:△ABC的三个顶点的坐标
分别为A(-4,1),B(-1,-1),C(-3,2),
依次连接A′,B′,C′便可得到所求作的三角形.
它们关于原点的对称点分别为
A′(4,-1),B′(1,1),C′(3,-2),
归纳总结
作关于原点对称的图形的步骤:
(1)写出各点关于原点对称的点的坐标;
(2)在坐标平面内描出这些对称点;
(3)参照原图形顺次连接各点,即为所求作的对称图形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.已知:如图,E(-4,2),F(-1,-1),以 O 为中心,作 △EFO 的关于
原点中心对称图形.
解:E′的坐标为(4,-2),
F′的坐标为(1,1)
依次连接O,E′,F′,
△E′F′O为△EFO的中心对称图形.
E′
F′
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
5.在如图所示编号为①、②、③、④的四个三角形中,关于y轴对称的两个
三角形的编号为 ;关于坐标原点O对称的两个三角形的编号为 .
y
x
-
1
-
2
-
4
-
3
-
5
-
1
-
2
-
4
-
5
-
3
1
2
4
3
5
1
2
4
3
5
O
①
②
③
④
①与②
①与③
典型例题
当堂检测
学习目标
课堂总结
概念剖析
关于原点对称的点的坐标
1.特征:P(x,y)关于原点的对称点为P'(-x,-y);
2.作图:作出关于原点对称的图形,先求出对称点的坐标再描点画图.
同课章节目录
