21.2.1 配方法 第2课时课件(共19张PPT)2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 21.2.1 配方法 第2课时课件(共19张PPT)2023-2024学年人教版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 383.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
第二十一章 一元二次方程
21.2.1 配方法
第2课时
1.知道配方法的概念,能运用配方法解一元二次方程.
2.通过用配方法将一元二次方程进行变形,进一步体会转化的思想方法.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
复习回顾
降次
直接开平方法
典型例题
当堂检测
学习目标
课堂总结
概念剖析
我们已经学会解形如 .因为它的左边是含有x的完全平方式,右边是非负数,所以可以直接降次解方程.那么,能否将x2+6x+4=0转化为可以直接降次的形式再求解呢?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解方程 x2+6x+4=0的过程可以用下面的框图表示:
x2+6x+4=0
x2+6x=-4
移项
两边加9(即 )使左边配成x2+2bx+b2的形式
x2+6x+9=-4+9
左边写成完全平方形式
(x+3)2=5
典型例题
当堂检测
学习目标
课堂总结
概念剖析
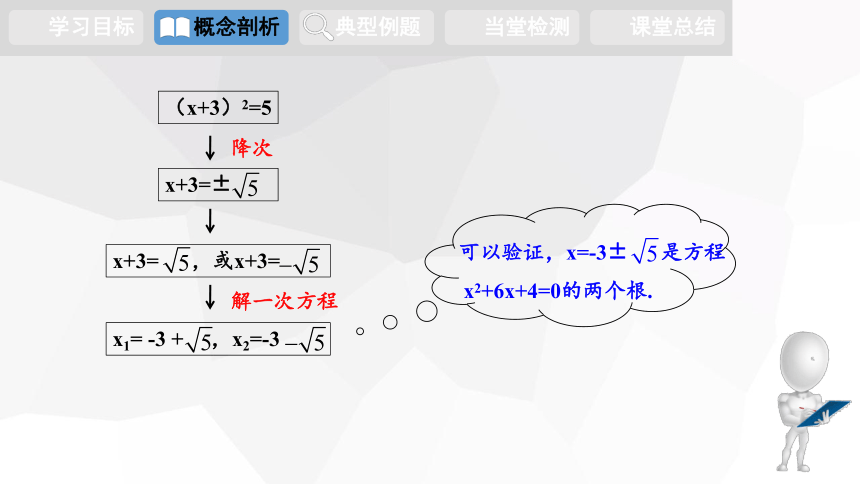
降次
解一次方程
x+3=±
x+3= ,或x+3=
x1= -3 + ,x2=-3
(x+3)2=5
可以验证,x=-3± 是方程
x2+6x+4=0的两个根.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
像上面那样,通过配成完全平方形式来解一元二次方程的方法,叫做配方法.可以看出,配方是为了降次,把一个一元二次方程转化为两个一元一次方程来解.
以上解法中,为什么在方程x2+6x+4=0两边加9?加其他数可以吗?
想一想
根据完全平方公式:9是一次项系数6一半的平方,加9正好与x2+6x能够配成x2+6x+9=(x+3)2,加其他数不行.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.解方程:
(1) x2+6x=-7 (2)2x2-4x-6=0
解:(1) 配方,得x2+6x+9=-7+9,
(x+3)2=2,
由此可得x+3=±
x1=-3+ ,x2=-3-
(2)移项,得2x2-4x=6,
二次项系数化为1,得 x2-2x=3,
配方,得(x-1)2=3+1
由此可得x-1=±2
x1=3,x2=-1;
典型例题
当堂检测
学习目标
课堂总结
概念剖析
用配方法解一元二次方程的一般步骤:
移项
二次项系数化为1
配方
直接开平方
方程左边为二次项和一次项,右边为常数项
左右两边同时除以二次项系数
方程两边都加上一次项系数一半的平方
如果右边是非负数直接开平方求出方程的解
归纳总结
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.解方程
(1)2x2-4x-1=0
解:(1)移项,得2x2-4x=1,
二次项系数化为1,得x2-2x=
配方,得(x-1)2=
由此可得x-1=
x1= ,x2=
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(2) x2-6x-7=0
(2)移项,得 x2-6x=7
二次项系数化为1,得x2-12x=14
配方,得(x-6)2=50
由此可得x-6=
x1= 6+ ,x2=6-
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.小明在解方程x2-2x-1=0时出现了错误,其解答过程如下:
x2-2x=-1 (第一步)
x2-2x+1=-1+1 (第二步)
(x-1)2=0 (第三步)
x1=x2=1 (第四步)
(1)小明解答过程是从第____步开始出错的,其错误原因是____________;
解:(1)一;不符合等式的性质1;
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(2)请写出x2-2x-1=0正确的解答过程.
解:(2)移项,得 x2-2x=1
配方,得(x-1)2=1+1
由此可得x-1=
x1= 1+ ,x2=1-
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.解方程:3x2﹣6x+4 =0.
解:移项,得3x2﹣6x =﹣4
二次项系数化为1,得x2﹣2x =﹣
配方,得,x2﹣2x+12 =﹣ +12
(x-1)2=﹣
4
3
4
3
1
3
因为实数的平方不会是负数,所以x取任何实数时,(x-1)2 都是非负数,该式都不成立,即原方程无实数根.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
一般地,如果一个一元二次方程通过配方转化成(x+n)2=p 的形式,
那么就有:
(1)当p>0时,方程有两个不等的实数根 x1=-n- ,x2=-n+ ;
(2)当p=0时,方程有两个相等的实数根:x1=x2=-n;
(3)当p<0时,因为对任意实数x,都有(x+n)2≥0,所以方程无实数根
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.已知关于x的方程3x2-6x+3p=0,其中p是常数.请用配方法解这个一元二次方程.
解:x2-2x=-p,
x2-2x+1=1-p,
(x-1)2=1-p,
当1-p>0,即p<1时,x-1=± ,所以x1=1+ ,x2=1-
当1-p = 0,即p=1时,x-1=0,所以x1=x2=1;
当1-p<0,即p<1时,方程无实数根.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例3.用配方法求证:代数式﹣10x2+7x﹣4的值恒小于0.
证明:原式=﹣10(x2﹣ x)﹣4
7
10
=﹣10[x2﹣ x+ ]﹣4+
7
10
7
20
( )2
49
40
=﹣10(x﹣ )2﹣
7
20
111
40
∵10(x﹣ )2 ≥0
7
20
∴﹣10(x﹣ )2 ≤0
7
20
即﹣10(x﹣ )2﹣ <0
7
20
111
40
故代数式﹣10x2+7x﹣4的值恒小于0.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.证明:对于任意实数x,代数式-3x2-x+1的值都不大于 .
证明:∵-3x2-x+1=-3(x2+ x)+1=-3(x2+ x+ )+ =-3(x+ )2+
又∵(x+ )2≥ 0
∴-3(x+ )2≤ 0
∴-3(x+ )2+ ≤
∴对于任意实数x,代数式-3x2-x+1的值都不大于 .
典型例题
当堂检测
学习目标
课堂总结
概念剖析
配方法
配方法解一元二次方程的基本思路
配方法解一元二次方程的一般步骤
典型例题
当堂检测
学习目标
课堂总结
概念剖析
第二十一章 一元二次方程
21.2.1 配方法
第2课时
1.知道配方法的概念,能运用配方法解一元二次方程.
2.通过用配方法将一元二次方程进行变形,进一步体会转化的思想方法.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
复习回顾
降次
直接开平方法
典型例题
当堂检测
学习目标
课堂总结
概念剖析
我们已经学会解形如 .因为它的左边是含有x的完全平方式,右边是非负数,所以可以直接降次解方程.那么,能否将x2+6x+4=0转化为可以直接降次的形式再求解呢?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解方程 x2+6x+4=0的过程可以用下面的框图表示:
x2+6x+4=0
x2+6x=-4
移项
两边加9(即 )使左边配成x2+2bx+b2的形式
x2+6x+9=-4+9
左边写成完全平方形式
(x+3)2=5
典型例题
当堂检测
学习目标
课堂总结
概念剖析
降次
解一次方程
x+3=±
x+3= ,或x+3=
x1= -3 + ,x2=-3
(x+3)2=5
可以验证,x=-3± 是方程
x2+6x+4=0的两个根.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
像上面那样,通过配成完全平方形式来解一元二次方程的方法,叫做配方法.可以看出,配方是为了降次,把一个一元二次方程转化为两个一元一次方程来解.
以上解法中,为什么在方程x2+6x+4=0两边加9?加其他数可以吗?
想一想
根据完全平方公式:9是一次项系数6一半的平方,加9正好与x2+6x能够配成x2+6x+9=(x+3)2,加其他数不行.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.解方程:
(1) x2+6x=-7 (2)2x2-4x-6=0
解:(1) 配方,得x2+6x+9=-7+9,
(x+3)2=2,
由此可得x+3=±
x1=-3+ ,x2=-3-
(2)移项,得2x2-4x=6,
二次项系数化为1,得 x2-2x=3,
配方,得(x-1)2=3+1
由此可得x-1=±2
x1=3,x2=-1;
典型例题
当堂检测
学习目标
课堂总结
概念剖析
用配方法解一元二次方程的一般步骤:
移项
二次项系数化为1
配方
直接开平方
方程左边为二次项和一次项,右边为常数项
左右两边同时除以二次项系数
方程两边都加上一次项系数一半的平方
如果右边是非负数直接开平方求出方程的解
归纳总结
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.解方程
(1)2x2-4x-1=0
解:(1)移项,得2x2-4x=1,
二次项系数化为1,得x2-2x=
配方,得(x-1)2=
由此可得x-1=
x1= ,x2=
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(2) x2-6x-7=0
(2)移项,得 x2-6x=7
二次项系数化为1,得x2-12x=14
配方,得(x-6)2=50
由此可得x-6=
x1= 6+ ,x2=6-
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.小明在解方程x2-2x-1=0时出现了错误,其解答过程如下:
x2-2x=-1 (第一步)
x2-2x+1=-1+1 (第二步)
(x-1)2=0 (第三步)
x1=x2=1 (第四步)
(1)小明解答过程是从第____步开始出错的,其错误原因是____________;
解:(1)一;不符合等式的性质1;
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(2)请写出x2-2x-1=0正确的解答过程.
解:(2)移项,得 x2-2x=1
配方,得(x-1)2=1+1
由此可得x-1=
x1= 1+ ,x2=1-
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.解方程:3x2﹣6x+4 =0.
解:移项,得3x2﹣6x =﹣4
二次项系数化为1,得x2﹣2x =﹣
配方,得,x2﹣2x+12 =﹣ +12
(x-1)2=﹣
4
3
4
3
1
3
因为实数的平方不会是负数,所以x取任何实数时,(x-1)2 都是非负数,该式都不成立,即原方程无实数根.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
一般地,如果一个一元二次方程通过配方转化成(x+n)2=p 的形式,
那么就有:
(1)当p>0时,方程有两个不等的实数根 x1=-n- ,x2=-n+ ;
(2)当p=0时,方程有两个相等的实数根:x1=x2=-n;
(3)当p<0时,因为对任意实数x,都有(x+n)2≥0,所以方程无实数根
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.已知关于x的方程3x2-6x+3p=0,其中p是常数.请用配方法解这个一元二次方程.
解:x2-2x=-p,
x2-2x+1=1-p,
(x-1)2=1-p,
当1-p>0,即p<1时,x-1=± ,所以x1=1+ ,x2=1-
当1-p = 0,即p=1时,x-1=0,所以x1=x2=1;
当1-p<0,即p<1时,方程无实数根.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例3.用配方法求证:代数式﹣10x2+7x﹣4的值恒小于0.
证明:原式=﹣10(x2﹣ x)﹣4
7
10
=﹣10[x2﹣ x+ ]﹣4+
7
10
7
20
( )2
49
40
=﹣10(x﹣ )2﹣
7
20
111
40
∵10(x﹣ )2 ≥0
7
20
∴﹣10(x﹣ )2 ≤0
7
20
即﹣10(x﹣ )2﹣ <0
7
20
111
40
故代数式﹣10x2+7x﹣4的值恒小于0.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.证明:对于任意实数x,代数式-3x2-x+1的值都不大于 .
证明:∵-3x2-x+1=-3(x2+ x)+1=-3(x2+ x+ )+ =-3(x+ )2+
又∵(x+ )2≥ 0
∴-3(x+ )2≤ 0
∴-3(x+ )2+ ≤
∴对于任意实数x,代数式-3x2-x+1的值都不大于 .
典型例题
当堂检测
学习目标
课堂总结
概念剖析
配方法
配方法解一元二次方程的基本思路
配方法解一元二次方程的一般步骤
典型例题
当堂检测
学习目标
课堂总结
概念剖析
同课章节目录
