24.1.1 圆 课件(共27张PPT) 2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 24.1.1 圆 课件(共27张PPT) 2023-2024学年人教版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 425.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 23:20:13 | ||
图片预览








文档简介
(共27张PPT)
九年级·数学·人教版·上册
24.1 圆的有关性质
单元概述 在学习本章之前,已通过折叠、对称、平移、旋转、推理证明等方式认识了许多图形的性质,积累了大量的空间与图形的经验.本章是在学习了这些直线型图形的有关性质的基础上,进一步来探索一种特殊的曲线——圆的有关性质.通过本章的学习,对我们今后继续学习数学,尤其是逐步树立分类讨论等数学思想起着良好的铺垫作用.本章的学习也是高中数学学习的基础
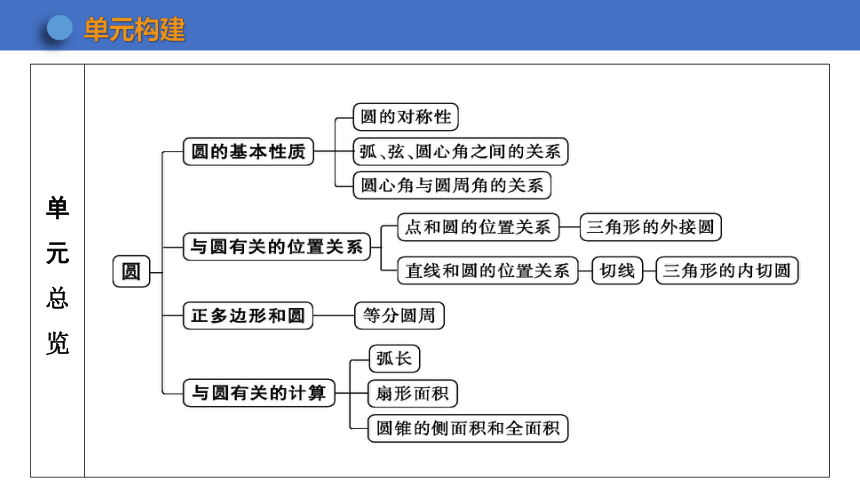
单元总览
24.1 圆的有关性质
24.1.1 圆(见学生用书P54)
1.经历形成圆的概念的过程,知道圆的两种定义.
2.认识弧(优弧、劣弧)、弦、半圆、直径、等圆、等弧等相关概念.
3.理解并掌握证明“几点共圆”的方法.
◎重点:圆的定义,等圆、弧、等弧、弦、半圆、半径等有关概念.
◎难点:证明“几个点在同一个圆上”的方法.
在前面的学习中,我们已经认识了各种类型的多边形,如:三角形、四边形、五边形、六边形等等.老师一边说导入语一边按照边数从少到多的顺序,用多媒体展示多边形的图片,当边数逐渐增多时,可以加快展示的速度,当边数足够多时,多边形逼近于圆,引入本节课学习的主题:一种完美的几何图形——圆.
圆的概念
认真阅读课本本课时“例1”之前的内容,解决下列问题.
1.根据自己对圆的概念的理解,以点O为圆心,线段a为半径画一个圆.
答:图略.
这个圆可以记作: ;读作: .
☉O
圆O
2.所画圆上每个点到点O的距离都相等吗 如果相等,都等于什么
答:都相等,都等于线段a的长度.
3.到点O的距离等于线段a的点在圆上吗 有没有不在圆上的
答:都在同一个圆上,没有不在圆上的.
揭示概念:(1)在一个平面内,线段绕它固定的一个端点旋转一周,另一个端点所形成的图形叫做 .其中固定的端点叫做 ,线段叫做 .
圆心
半径
圆
(2)圆可以看成是所有到 的距离等于 的点的集合.其中这个定点叫做 ,这个定长叫做 .其中,圆心决定圆的位置,半径决定圆的大小.
定点
定长
圆心
半径
圆的有关概念
认真阅读课本本课时“例1”下面的三个自然段,结合图形理解圆的有关概念后,独立完成下面的题目.
1.连接圆上任意两点的线段叫做 ,经过圆心的弦叫做 直径 .
弦
2.圆上任意两点间的部分叫做 ,简称 .圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做 .大于半圆的弧叫做 ,小于半圆的弧叫做 .
3.能够重合的两个圆叫做 .半径 的两个圆是等圆;同圆或等圆的半径 .
4. 在同圆或等圆中,能够互相重合的弧叫做 .
圆弧
弧
半圆
优弧
劣弧
等圆
相等
相等
等弧
与圆有关的概念的理解和辨析(直径与弦、半圆与弧的关系)
1.有下列说法:①直径是弦;②弦是直径;③半圆是弧,但弧不一定是半圆;④长度相等的两条弧是等弧.其中正确的命题有( )
A.1个 B.2个 C.3个 D.4个
B
方法归纳交流 (1)等弧是指能 的两条弧,所以不仅仅要求长度相等,还要求保证弯曲的弧度相同.
(2)直径是弦,是圆中最 的弦.
(3)弧可分为劣弧、半圆和优弧,半圆是弧.
重合
长
变式演练 下列命题中,正确的有 ( )
①弦是圆上任意两点之间的部分;②半径是弦;③直径是一个圆内最长的弦;④弧是半圆,半圆是弧.
A.1个 B.2个 C.3个 D.4个
A
证明点在已知圆上的方法
2.如图,在四边形ABCD中,∠A=∠C=90°.求证:A、B、C、D四个点在同一个圆上.
证明:如图,连接BD,取BD的中点O,连接OA、OC.
∵∠BAD=∠BCD=90°,OB=OD,
∴OA=OB=OD=OC,
∴A、B、C、D四个点在同一个圆上.
方法归纳交流 利用圆的定义,证明几点在同一个圆上的方法:证明这几个点到某一个点的距离 .
相等
利用圆的概念解决简单的几何问题
3.如图,在☉O中,AB为弦,C,D两点在AB上,且∠AOC=∠BOD.
求证:△OAC≌△OBD.
证明:∵OA=OB,
∴∠A=∠B.
又∵∠AOC=∠BOD,
∴△OAC≌△OBD.
变式演练
1.如图,AB是☉O的弦,半径OC、OD分别交AB于点E,F,且AE=BF,请你判断线段OE与OF的数量关系,并给予证明.
解:OE=OF.
证明:如图,连接OA、OB,∵OA=OB,
∴∠OAE=∠OBF.
又∵AE=BF,∴△OAE≌△OBF,
∴OE=OF.
2.如图,线段AD过圆心O,交☉O于D,C两点,∠EOD=78°,AE交☉O于点B,且AB=OC,求∠A的度数.
解:如图,连接OB.
∵AB=OC,OB=OC,
∴AB=OB,∴∠BOA=∠A.
又∵OB=OE,
∴∠E=∠EBO=∠BOA+∠A=2∠A,
∴∠EOD=∠E+∠A=3∠A.
即3∠A=78°,∴∠A=26°.
方法归纳交流 因为圆中的半径都相等,所以在圆中易得
三角形,这样就可以把圆中的部分问题转化为三角形的问题.
等腰
九年级·数学·人教版·上册
24.1 圆的有关性质
单元概述 在学习本章之前,已通过折叠、对称、平移、旋转、推理证明等方式认识了许多图形的性质,积累了大量的空间与图形的经验.本章是在学习了这些直线型图形的有关性质的基础上,进一步来探索一种特殊的曲线——圆的有关性质.通过本章的学习,对我们今后继续学习数学,尤其是逐步树立分类讨论等数学思想起着良好的铺垫作用.本章的学习也是高中数学学习的基础
单元总览
24.1 圆的有关性质
24.1.1 圆(见学生用书P54)
1.经历形成圆的概念的过程,知道圆的两种定义.
2.认识弧(优弧、劣弧)、弦、半圆、直径、等圆、等弧等相关概念.
3.理解并掌握证明“几点共圆”的方法.
◎重点:圆的定义,等圆、弧、等弧、弦、半圆、半径等有关概念.
◎难点:证明“几个点在同一个圆上”的方法.
在前面的学习中,我们已经认识了各种类型的多边形,如:三角形、四边形、五边形、六边形等等.老师一边说导入语一边按照边数从少到多的顺序,用多媒体展示多边形的图片,当边数逐渐增多时,可以加快展示的速度,当边数足够多时,多边形逼近于圆,引入本节课学习的主题:一种完美的几何图形——圆.
圆的概念
认真阅读课本本课时“例1”之前的内容,解决下列问题.
1.根据自己对圆的概念的理解,以点O为圆心,线段a为半径画一个圆.
答:图略.
这个圆可以记作: ;读作: .
☉O
圆O
2.所画圆上每个点到点O的距离都相等吗 如果相等,都等于什么
答:都相等,都等于线段a的长度.
3.到点O的距离等于线段a的点在圆上吗 有没有不在圆上的
答:都在同一个圆上,没有不在圆上的.
揭示概念:(1)在一个平面内,线段绕它固定的一个端点旋转一周,另一个端点所形成的图形叫做 .其中固定的端点叫做 ,线段叫做 .
圆心
半径
圆
(2)圆可以看成是所有到 的距离等于 的点的集合.其中这个定点叫做 ,这个定长叫做 .其中,圆心决定圆的位置,半径决定圆的大小.
定点
定长
圆心
半径
圆的有关概念
认真阅读课本本课时“例1”下面的三个自然段,结合图形理解圆的有关概念后,独立完成下面的题目.
1.连接圆上任意两点的线段叫做 ,经过圆心的弦叫做 直径 .
弦
2.圆上任意两点间的部分叫做 ,简称 .圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做 .大于半圆的弧叫做 ,小于半圆的弧叫做 .
3.能够重合的两个圆叫做 .半径 的两个圆是等圆;同圆或等圆的半径 .
4. 在同圆或等圆中,能够互相重合的弧叫做 .
圆弧
弧
半圆
优弧
劣弧
等圆
相等
相等
等弧
与圆有关的概念的理解和辨析(直径与弦、半圆与弧的关系)
1.有下列说法:①直径是弦;②弦是直径;③半圆是弧,但弧不一定是半圆;④长度相等的两条弧是等弧.其中正确的命题有( )
A.1个 B.2个 C.3个 D.4个
B
方法归纳交流 (1)等弧是指能 的两条弧,所以不仅仅要求长度相等,还要求保证弯曲的弧度相同.
(2)直径是弦,是圆中最 的弦.
(3)弧可分为劣弧、半圆和优弧,半圆是弧.
重合
长
变式演练 下列命题中,正确的有 ( )
①弦是圆上任意两点之间的部分;②半径是弦;③直径是一个圆内最长的弦;④弧是半圆,半圆是弧.
A.1个 B.2个 C.3个 D.4个
A
证明点在已知圆上的方法
2.如图,在四边形ABCD中,∠A=∠C=90°.求证:A、B、C、D四个点在同一个圆上.
证明:如图,连接BD,取BD的中点O,连接OA、OC.
∵∠BAD=∠BCD=90°,OB=OD,
∴OA=OB=OD=OC,
∴A、B、C、D四个点在同一个圆上.
方法归纳交流 利用圆的定义,证明几点在同一个圆上的方法:证明这几个点到某一个点的距离 .
相等
利用圆的概念解决简单的几何问题
3.如图,在☉O中,AB为弦,C,D两点在AB上,且∠AOC=∠BOD.
求证:△OAC≌△OBD.
证明:∵OA=OB,
∴∠A=∠B.
又∵∠AOC=∠BOD,
∴△OAC≌△OBD.
变式演练
1.如图,AB是☉O的弦,半径OC、OD分别交AB于点E,F,且AE=BF,请你判断线段OE与OF的数量关系,并给予证明.
解:OE=OF.
证明:如图,连接OA、OB,∵OA=OB,
∴∠OAE=∠OBF.
又∵AE=BF,∴△OAE≌△OBF,
∴OE=OF.
2.如图,线段AD过圆心O,交☉O于D,C两点,∠EOD=78°,AE交☉O于点B,且AB=OC,求∠A的度数.
解:如图,连接OB.
∵AB=OC,OB=OC,
∴AB=OB,∴∠BOA=∠A.
又∵OB=OE,
∴∠E=∠EBO=∠BOA+∠A=2∠A,
∴∠EOD=∠E+∠A=3∠A.
即3∠A=78°,∴∠A=26°.
方法归纳交流 因为圆中的半径都相等,所以在圆中易得
三角形,这样就可以把圆中的部分问题转化为三角形的问题.
等腰
同课章节目录
