24.1.2 垂直于弦的直径 课件(共16张PPT) 2023-—2024学年人教版数学九年级上册
文档属性
| 名称 | 24.1.2 垂直于弦的直径 课件(共16张PPT) 2023-—2024学年人教版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 498.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
第二十四章 圆
24.1 圆的有关性质
24.1.2 垂直于弦的直径
1.进一步认识圆,了解圆是轴对称图形;
2.理解垂直于弦的直径的性质和推论,并能应用它解决一些简单
的计算、证明和作图问题;(重点)
3. 灵活运用垂径定理解决有关圆的问题.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
问题引入:
如图,剪一个圆形纸片,沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得出什么结论?你能证明你的结论吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(一)圆的对称性
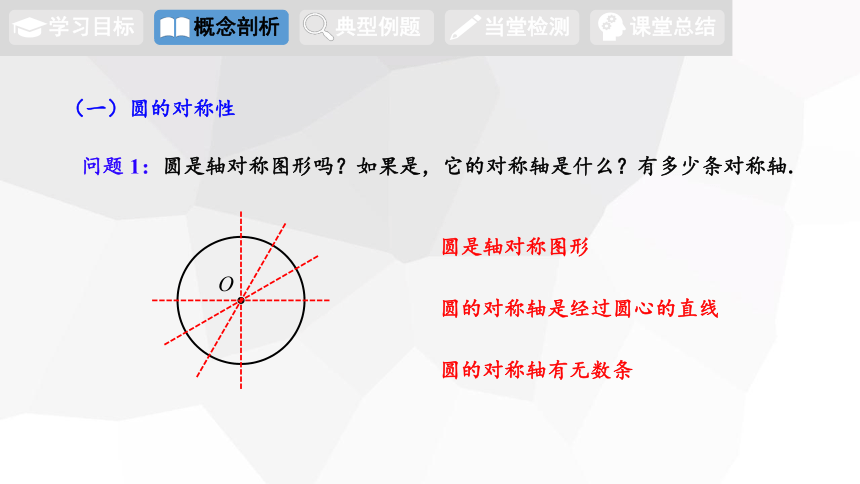
问题 1:圆是轴对称图形吗?如果是,它的对称轴是什么?有多少条对称轴.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
圆是轴对称图形
O
圆的对称轴是经过圆心的直线
圆的对称轴有无数条
典型例题
当堂检测
学习目标
课堂总结
概念剖析
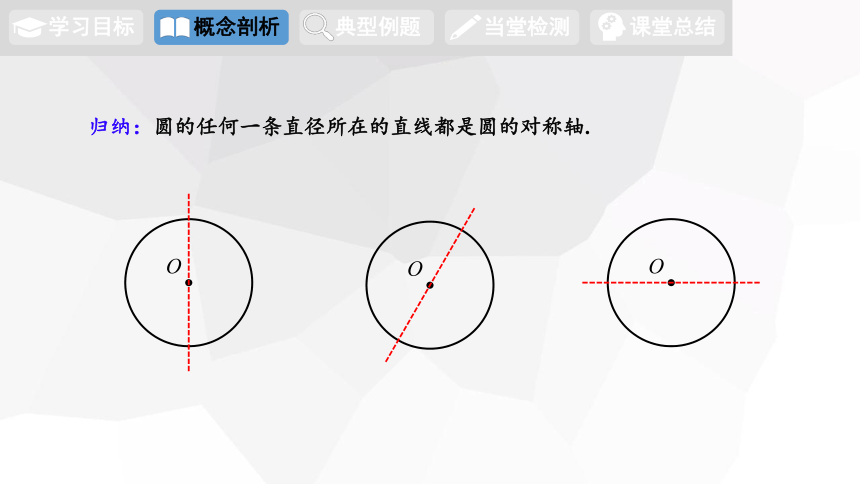
归纳:圆的任何一条直径所在的直线都是圆的对称轴.
O
O
O
(二)垂径定理
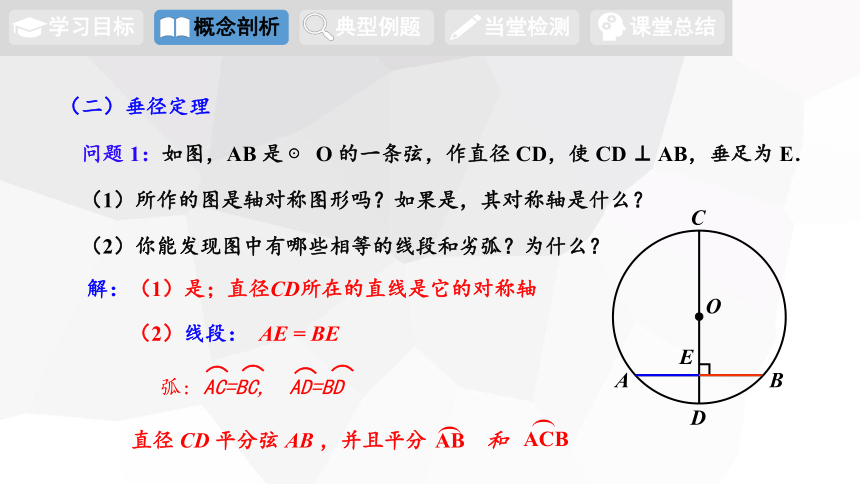
问题 1:如图,AB 是 ⊙ O 的一条弦,作直径 CD,使 CD ⊥ AB,垂足为 E.
(1)所作的图是轴对称图形吗?如果是,其对称轴是什么?
(2)你能发现图中有哪些相等的线段和劣弧?为什么?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(2)线段: AE = BE
解:(1)是;直径CD所在的直线是它的对称轴
·
O
A
B
C
D
E
弧: AC=BC, AD=BD
⌒
⌒
⌒
⌒
直径 CD 平分弦 AB ,并且平分 和
AB
(
ACB
(
典型例题
当堂检测
学习目标
课堂总结
概念剖析
·
O
A
B
C
D
E
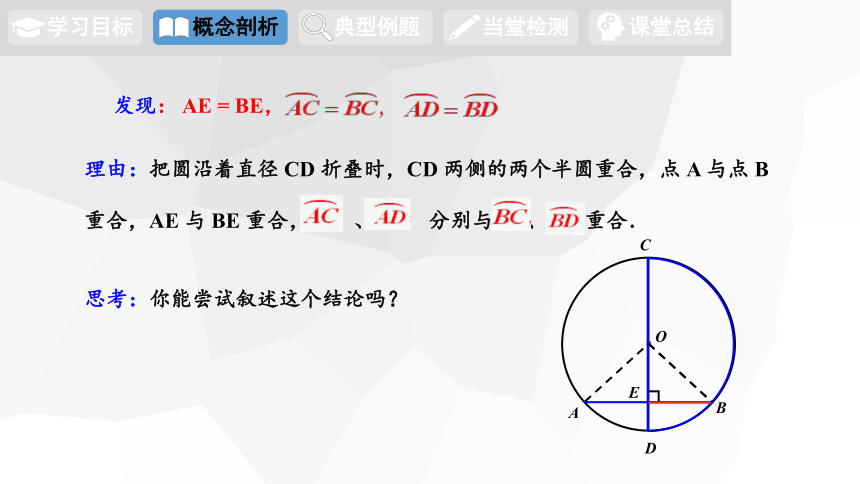
思考:你能尝试叙述这个结论吗?
发现: AE = BE,
理由:把圆沿着直径 CD 折叠时,CD 两侧的两个半圆重合,点 A 与点 B 重合,AE 与 BE 重合, 、 分别与 、 重合.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
垂径定理:
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
∵ CD是直径,CD⊥AB
符号语言:
∴ AE = BE,
归纳总结
推论:平分这条弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1. “不是直径”这个条件能去掉吗?如果不能,请举出反例.
·
O
A
B
C
D
① CD是直径,② CD⊥AB,③ AE = BE;
⌒
⌒
④ AC = BC,⑤ AD = BD.
⌒
⌒
2. 如果具备下面五个条件中的任何两个,那么一定可以得到其他三个结论吗?
思考
·
O
A
B
C
D
E
典型例题
当堂检测
学习目标
课堂总结
概念剖析
试一试:
1.下列图形是否具备垂径定理的条件?如果不是,请说明为什么?
是
不是,因为没有垂直
是
不是, 因为CD没有过圆心
注意:垂径定理的本质:
(1)过圆心 ;(2)垂直于弦;(3)平分弦;
(4)平分弦所对的优弧;(4)平分弦所对的劣弧.
满足其中任两条,
必定同时满足另三条
典型例题
当堂检测
学习目标
课堂总结
概念剖析
能运用垂径定理的几个基本图形:
归纳总结
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例 1:赵州桥主桥拱的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离)为 7.2 m,你能求出赵州桥主桥拱的半径吗?
(一)垂径定理
37.4
7.2
R
D
分析:如图,用弧AB表示主桥拱,则弦AB即是跨度,设 所在圆的圆心为O,半径为R;
经过圆心O作弦AB的垂线OC,D为垂足,OC与弦AB相交于点C;
根据前面的结论可知,D是弦AB的中点,C是 的中点,CD就是拱高.
AB
(
AB
(
典型例题
当堂检测
学习目标
课堂总结
概念剖析
已知:弦 AB = 37.4m,拱高 CD 为 7.2 m,求赵州桥主桥拱的半径 R.
18.7
R–7.2
37.4
7.2
R
D
R
解得:R ≈ 27.9 ;
在 Rt△OAD中,由勾股定理,得:
即:R2 = 18.72 + (R – 7.2)2,
因此,赵州桥的主桥拱半径约为27.9 m.
OA2 = AD2 + OD2
OD = OC – CD = R – 7.2
弦 AB = 37.4 m,CD = 7.2 m,
解:如图,设半径为 R,
则: (m),
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2. 如图,在 ⊙ O 中,弦 AB 的长为 8 cm,圆心 O 到弦 AB 的距离为 3 cm,求 ⊙ O 的半径.
·
O
A
B
E
解:连接AO,作 OE ⊥ AB 于点 E,
答:⊙O的半径为5 cm.
在 Rt△AOE 中,
得:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
在圆中有关弦长 a,半径 r, 弦心距 d(圆心到弦的距离)的计算题时,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.
方法归纳
1. 涉及垂径定理的辅助线添加:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
垂径定理:
(1)内容:垂直于弦的直径平分弦,并且平分弦所对的两条弧
(2)推论:一条直线满足:① 过圆心;② 垂直于弦;
③ 平分弦(不是直径);④ 平分弦所对的优弧;⑤ 平分弦所对的劣弧;
满足其中两个条件就可以推出其它三个结论(“知二推三”)
(3)辅助线:两条辅助线:连半径,作弦心距;
(4)基本图形及变式图形:构造Rt△利用勾股定理计算或建立方程.
第二十四章 圆
24.1 圆的有关性质
24.1.2 垂直于弦的直径
1.进一步认识圆,了解圆是轴对称图形;
2.理解垂直于弦的直径的性质和推论,并能应用它解决一些简单
的计算、证明和作图问题;(重点)
3. 灵活运用垂径定理解决有关圆的问题.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
问题引入:
如图,剪一个圆形纸片,沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得出什么结论?你能证明你的结论吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(一)圆的对称性
问题 1:圆是轴对称图形吗?如果是,它的对称轴是什么?有多少条对称轴.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
圆是轴对称图形
O
圆的对称轴是经过圆心的直线
圆的对称轴有无数条
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳:圆的任何一条直径所在的直线都是圆的对称轴.
O
O
O
(二)垂径定理
问题 1:如图,AB 是 ⊙ O 的一条弦,作直径 CD,使 CD ⊥ AB,垂足为 E.
(1)所作的图是轴对称图形吗?如果是,其对称轴是什么?
(2)你能发现图中有哪些相等的线段和劣弧?为什么?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(2)线段: AE = BE
解:(1)是;直径CD所在的直线是它的对称轴
·
O
A
B
C
D
E
弧: AC=BC, AD=BD
⌒
⌒
⌒
⌒
直径 CD 平分弦 AB ,并且平分 和
AB
(
ACB
(
典型例题
当堂检测
学习目标
课堂总结
概念剖析
·
O
A
B
C
D
E
思考:你能尝试叙述这个结论吗?
发现: AE = BE,
理由:把圆沿着直径 CD 折叠时,CD 两侧的两个半圆重合,点 A 与点 B 重合,AE 与 BE 重合, 、 分别与 、 重合.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
垂径定理:
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
∵ CD是直径,CD⊥AB
符号语言:
∴ AE = BE,
归纳总结
推论:平分这条弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1. “不是直径”这个条件能去掉吗?如果不能,请举出反例.
·
O
A
B
C
D
① CD是直径,② CD⊥AB,③ AE = BE;
⌒
⌒
④ AC = BC,⑤ AD = BD.
⌒
⌒
2. 如果具备下面五个条件中的任何两个,那么一定可以得到其他三个结论吗?
思考
·
O
A
B
C
D
E
典型例题
当堂检测
学习目标
课堂总结
概念剖析
试一试:
1.下列图形是否具备垂径定理的条件?如果不是,请说明为什么?
是
不是,因为没有垂直
是
不是, 因为CD没有过圆心
注意:垂径定理的本质:
(1)过圆心 ;(2)垂直于弦;(3)平分弦;
(4)平分弦所对的优弧;(4)平分弦所对的劣弧.
满足其中任两条,
必定同时满足另三条
典型例题
当堂检测
学习目标
课堂总结
概念剖析
能运用垂径定理的几个基本图形:
归纳总结
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例 1:赵州桥主桥拱的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离)为 7.2 m,你能求出赵州桥主桥拱的半径吗?
(一)垂径定理
37.4
7.2
R
D
分析:如图,用弧AB表示主桥拱,则弦AB即是跨度,设 所在圆的圆心为O,半径为R;
经过圆心O作弦AB的垂线OC,D为垂足,OC与弦AB相交于点C;
根据前面的结论可知,D是弦AB的中点,C是 的中点,CD就是拱高.
AB
(
AB
(
典型例题
当堂检测
学习目标
课堂总结
概念剖析
已知:弦 AB = 37.4m,拱高 CD 为 7.2 m,求赵州桥主桥拱的半径 R.
18.7
R–7.2
37.4
7.2
R
D
R
解得:R ≈ 27.9 ;
在 Rt△OAD中,由勾股定理,得:
即:R2 = 18.72 + (R – 7.2)2,
因此,赵州桥的主桥拱半径约为27.9 m.
OA2 = AD2 + OD2
OD = OC – CD = R – 7.2
弦 AB = 37.4 m,CD = 7.2 m,
解:如图,设半径为 R,
则: (m),
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2. 如图,在 ⊙ O 中,弦 AB 的长为 8 cm,圆心 O 到弦 AB 的距离为 3 cm,求 ⊙ O 的半径.
·
O
A
B
E
解:连接AO,作 OE ⊥ AB 于点 E,
答:⊙O的半径为5 cm.
在 Rt△AOE 中,
得:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
在圆中有关弦长 a,半径 r, 弦心距 d(圆心到弦的距离)的计算题时,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.
方法归纳
1. 涉及垂径定理的辅助线添加:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
垂径定理:
(1)内容:垂直于弦的直径平分弦,并且平分弦所对的两条弧
(2)推论:一条直线满足:① 过圆心;② 垂直于弦;
③ 平分弦(不是直径);④ 平分弦所对的优弧;⑤ 平分弦所对的劣弧;
满足其中两个条件就可以推出其它三个结论(“知二推三”)
(3)辅助线:两条辅助线:连半径,作弦心距;
(4)基本图形及变式图形:构造Rt△利用勾股定理计算或建立方程.
同课章节目录
