24.1.4 第1课时 圆周角定理 课件(共16张PPT) 2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 24.1.4 第1课时 圆周角定理 课件(共16张PPT) 2023-2024学年人教版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 264.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 23:22:58 | ||
图片预览




文档简介
(共16张PPT)
第二十四章 圆
24.1 圆的有关性质
24.1.4 圆周角 第1课时
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系,并能运用圆周角定理解决简单
的几何问题.(重点)
3.理解并掌握圆周角定理的推论及其证明过程和运用.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
回顾:
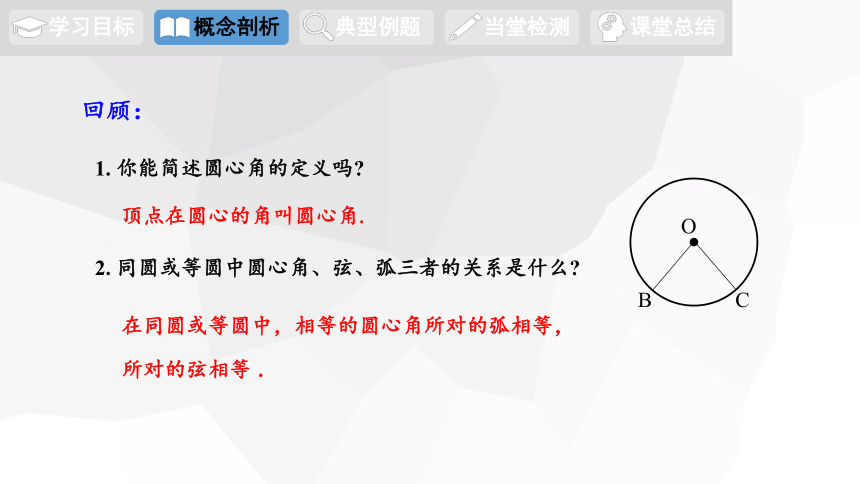
1. 你能简述圆心角的定义吗
顶点在圆心的角叫圆心角.
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等 .
2. 同圆或等圆中圆心角、弦、弧三者的关系是什么
O
B
C
思考:圆心角顶点发生变化时,我们能得到几种情况
说一说:图中的变化后的 ∠BAC 的顶点 A 各在圆的什么位置?角的两边和圆是什么关系?
B
C
A
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(一)圆周角的定义及性质
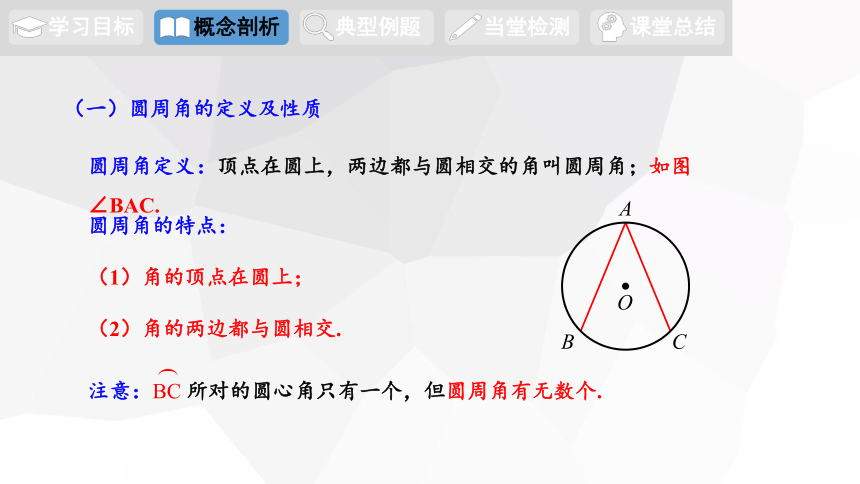
圆周角定义:顶点在圆上,两边都与圆相交的角叫圆周角;如图 ∠BAC.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
圆周角的特点:
(1)角的顶点在圆上;
(2)角的两边都与圆相交.
O
B
A
C
注意:BC 所对的圆心角只有一个,但圆周角有无数个.
(
圆周角性质:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
A
B
C
解:∵ ∠AOC是△ABO的外角,∴ ∠AOC = ∠B + ∠A;∵ OA = OB,∴ ∠A = ∠B;
∴ ∠AOC = 2∠B.
即∠ABC = ∠AOC.
(1)特殊情况: 当圆心 O 在圆周角 ∠ABC 的一边BC上时,
圆周角∠ABC与圆心角∠AOC的大小关系.
思考:如果圆心不在圆周角的一边上,结果会怎样
分析:可将右图转化为(1)的情况;
D
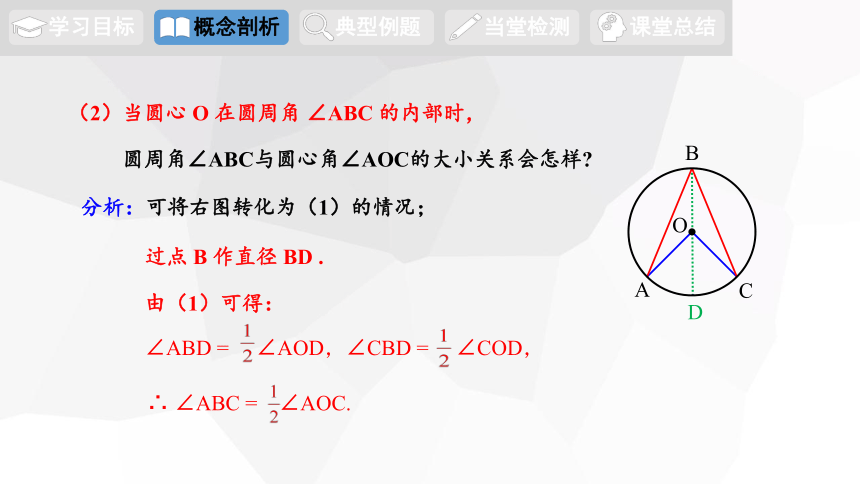
(2)当圆心 O 在圆周角 ∠ABC 的内部时,
圆周角∠ABC与圆心角∠AOC的大小关系会怎样
过点 B 作直径 BD .
由(1)可得:
∠ABD = ∠AOD,∠CBD = ∠COD,
∴ ∠ABC = ∠AOC.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
A
B
C
分析:可将右图转化为(1)的情况;
D
(3)当圆心 O 在圆周角 ∠ABC 的外部时,
圆周角∠ABC与圆心角∠AOC的大小关系会怎样
过点 B 作直径 BD .
由(1)可得:
∠ABD = ∠AOD,∠CBD = ∠COD,
∴ ∠ABC = ∠AOC.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
A
B
C
思考:通过上述 3 种情况的探索,你有什么发现吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结:
圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.
O
B
A
C
O
B
A
C
O
B
A
C
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例 1:如图所示,点 A,B,C 均在☉O上,∠OAB = 46°. 求∠ACB的度数.
(一)圆周角的定义及性质
O
A
C
B
解:如图所示,连接OB;
∵ OA = OB,
∴ ∠OAB = ∠OBA;
∵ ∠OAB = 46°,
∴ ∠AOB = 180°– 2∠OAB = 88°.
∴ ∠ACB = ∠AOB = 44°.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1. 如图所示,点 A,B,C 都在☉O上,若∠C = 35°,求 ∠AOB 的度数.
解:∵ ∠C与 ∠AOB是 AB 所对的圆周角和圆心角,
∴ 由圆周角定理可得:∠AOB = 2∠C = 70°.
O
A
C
B
(二)圆周角定理的推论
推论 1:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
应用:
∵ ∠FAE = ∠CDB,
E
A
B
O
F
C
D
BC
(
EF
(
=
∴
推论 2:半圆或直径所对的圆周角是直角,90°的圆周角所对的弦是直径.
∵ AB 是直径
∴ ∠AC1B = 90°
∵ ∠AC1B = 90°
∴ AB 是直径.
用于判断某个圆周角是否是直角;
典型例题
当堂检测
学习目标
课堂总结
概念剖析
应用:
·
A
B
C1
O
C2
C3
用于判断某条弦是否是直径.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例 2:如图所示,AB 是 ☉O 的直径,BD 是 ☉O 的弦,延长 BD 到 C,使 AC = AB,BD 与 CD 的大小有什么关系 为什么
(二)圆周角定理的推论
证明:BD = CD;
理由如下:连接AD,∵ AB 是 ☉O 的直径,
∴ ∠ADB = 90°,即 AD ⊥ BC;
又∵ AC = AB,
∴ △ABC是等腰三角形,∴ BD = CD.
A
B
C
O
D
方法归纳:在圆中,常作直径所对的圆周角,构造直角后利用三角形的性质求解.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2. 如图,已知 BD 是 ⊙O 的直径,⊙O 的弦 AC ⊥ BD 于点 E,若 ∠AOD = 60°,则 ∠DBC 的度数为( )
A. 30° B. 40° C.50° D.60°
A
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1. 圆周角的定义:
顶点在圆上,并且两边都与圆相交的角叫做圆周角;
2. 圆周角定理及推论:
圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.
推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等;
推论2:半圆或直径所对的圆周角是直角,90°的圆周角所对的弦是直径.
第二十四章 圆
24.1 圆的有关性质
24.1.4 圆周角 第1课时
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系,并能运用圆周角定理解决简单
的几何问题.(重点)
3.理解并掌握圆周角定理的推论及其证明过程和运用.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
回顾:
1. 你能简述圆心角的定义吗
顶点在圆心的角叫圆心角.
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等 .
2. 同圆或等圆中圆心角、弦、弧三者的关系是什么
O
B
C
思考:圆心角顶点发生变化时,我们能得到几种情况
说一说:图中的变化后的 ∠BAC 的顶点 A 各在圆的什么位置?角的两边和圆是什么关系?
B
C
A
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(一)圆周角的定义及性质
圆周角定义:顶点在圆上,两边都与圆相交的角叫圆周角;如图 ∠BAC.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
圆周角的特点:
(1)角的顶点在圆上;
(2)角的两边都与圆相交.
O
B
A
C
注意:BC 所对的圆心角只有一个,但圆周角有无数个.
(
圆周角性质:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
A
B
C
解:∵ ∠AOC是△ABO的外角,∴ ∠AOC = ∠B + ∠A;∵ OA = OB,∴ ∠A = ∠B;
∴ ∠AOC = 2∠B.
即∠ABC = ∠AOC.
(1)特殊情况: 当圆心 O 在圆周角 ∠ABC 的一边BC上时,
圆周角∠ABC与圆心角∠AOC的大小关系.
思考:如果圆心不在圆周角的一边上,结果会怎样
分析:可将右图转化为(1)的情况;
D
(2)当圆心 O 在圆周角 ∠ABC 的内部时,
圆周角∠ABC与圆心角∠AOC的大小关系会怎样
过点 B 作直径 BD .
由(1)可得:
∠ABD = ∠AOD,∠CBD = ∠COD,
∴ ∠ABC = ∠AOC.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
A
B
C
分析:可将右图转化为(1)的情况;
D
(3)当圆心 O 在圆周角 ∠ABC 的外部时,
圆周角∠ABC与圆心角∠AOC的大小关系会怎样
过点 B 作直径 BD .
由(1)可得:
∠ABD = ∠AOD,∠CBD = ∠COD,
∴ ∠ABC = ∠AOC.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
A
B
C
思考:通过上述 3 种情况的探索,你有什么发现吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结:
圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.
O
B
A
C
O
B
A
C
O
B
A
C
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例 1:如图所示,点 A,B,C 均在☉O上,∠OAB = 46°. 求∠ACB的度数.
(一)圆周角的定义及性质
O
A
C
B
解:如图所示,连接OB;
∵ OA = OB,
∴ ∠OAB = ∠OBA;
∵ ∠OAB = 46°,
∴ ∠AOB = 180°– 2∠OAB = 88°.
∴ ∠ACB = ∠AOB = 44°.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1. 如图所示,点 A,B,C 都在☉O上,若∠C = 35°,求 ∠AOB 的度数.
解:∵ ∠C与 ∠AOB是 AB 所对的圆周角和圆心角,
∴ 由圆周角定理可得:∠AOB = 2∠C = 70°.
O
A
C
B
(二)圆周角定理的推论
推论 1:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
应用:
∵ ∠FAE = ∠CDB,
E
A
B
O
F
C
D
BC
(
EF
(
=
∴
推论 2:半圆或直径所对的圆周角是直角,90°的圆周角所对的弦是直径.
∵ AB 是直径
∴ ∠AC1B = 90°
∵ ∠AC1B = 90°
∴ AB 是直径.
用于判断某个圆周角是否是直角;
典型例题
当堂检测
学习目标
课堂总结
概念剖析
应用:
·
A
B
C1
O
C2
C3
用于判断某条弦是否是直径.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例 2:如图所示,AB 是 ☉O 的直径,BD 是 ☉O 的弦,延长 BD 到 C,使 AC = AB,BD 与 CD 的大小有什么关系 为什么
(二)圆周角定理的推论
证明:BD = CD;
理由如下:连接AD,∵ AB 是 ☉O 的直径,
∴ ∠ADB = 90°,即 AD ⊥ BC;
又∵ AC = AB,
∴ △ABC是等腰三角形,∴ BD = CD.
A
B
C
O
D
方法归纳:在圆中,常作直径所对的圆周角,构造直角后利用三角形的性质求解.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2. 如图,已知 BD 是 ⊙O 的直径,⊙O 的弦 AC ⊥ BD 于点 E,若 ∠AOD = 60°,则 ∠DBC 的度数为( )
A. 30° B. 40° C.50° D.60°
A
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1. 圆周角的定义:
顶点在圆上,并且两边都与圆相交的角叫做圆周角;
2. 圆周角定理及推论:
圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.
推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等;
推论2:半圆或直径所对的圆周角是直角,90°的圆周角所对的弦是直径.
同课章节目录
