24.2.2 第1课时 直线和圆的三种位置关系课件(共16张PPT)2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 24.2.2 第1课时 直线和圆的三种位置关系课件(共16张PPT)2023-2024学年人教版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 370.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 23:23:41 | ||
图片预览





文档简介
(共16张PPT)
九年级·数学·人教版·上册
24.2.2 直线和圆的位置关系
第1课时 直线和圆的三种位置关系
1.知道直线和圆相离、相切、相交的概念、性质和判定方法.
2.探索直线和圆的位置关系,圆心到直线的距离和圆的半径之间的数量关系,并能利用它们解决问题.
◎重点:直线和圆的三种位置关系及其判定方法.
◎难点:直线和圆的三种位置关系的综合应用.
多媒体展示太阳从地平线或海平面升起的情景(或日落时的情况),并从中截取不同的画面,从而引入课题——直线和圆的位置关系.
直线和圆的位置关系
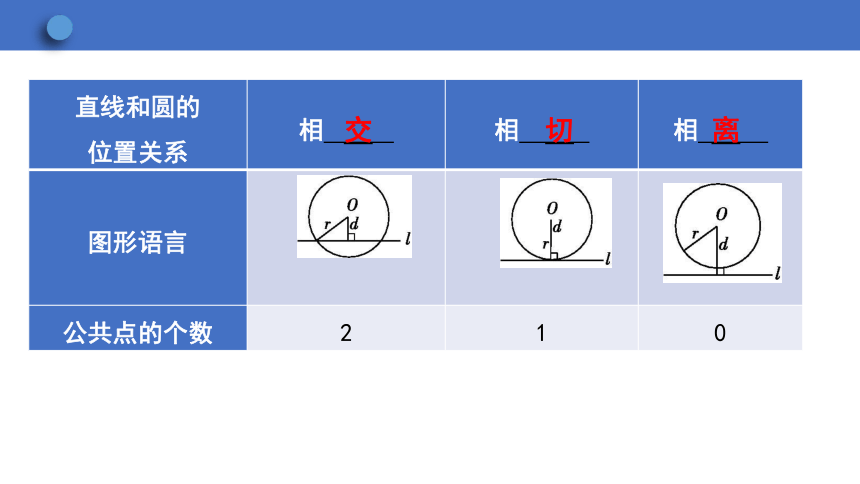
认真阅读课本中本课时的内容,理解“直线和圆的三种位置关系”,尝试独立完成下表.
直线和圆的 位置关系 相 相 相
图形语言
公共点的个数 2 1 0
交
切
离
圆心到直线 l的距离d与 半径r的关系 d r d r d r
公共点的名称
直线的名称
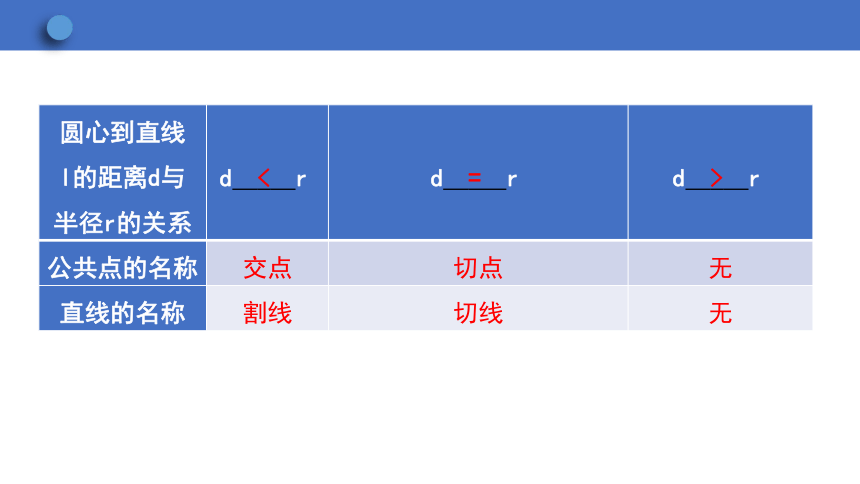
圆心到直线 l的距离d与 半径r的关系 d < r d = r d > r
公共点的名称 交点 切点 无
直线的名称 割线 切线 无
直线和圆的位置关系的判断
1.已知Rt△ABC的斜边AB=6 cm,直角边AC=3 cm.
(1)以C为圆心,以2 cm长为半径的圆和AB的位置关系是 ;
(2)以C为圆心,以4 cm长为半径的圆和AB的位置关系是 ;
相离
相交
(3)以C为圆心,以 cm长为半径的圆和AB的位置关系是相切.
方法归纳交流 判断直线与圆的位置关系的方法:当无法确定直线和圆有几个公共点时,通常过圆心作直线的垂线,计算
的长度,再比较垂线段的长与半径的大小关系即可.
垂线段
变式演练 已知☉O的半径为2,直线l上有一点P满足PO=2,则直线l与☉O的位置关系是( )
A.相切 B.相离
C.相离或相切 D.相切或相交
D
直线和圆的位置关系中的动态问题
2.
如图,在直角坐标系中,☉A的半径为2,圆心坐标为(4,0),y轴上有点B(0,3),点C是☉A上的动点,点P是BC的中点,则OP的范围是( )
A
A.≤OP≤
B.2≤OP≤4
C.≤OP≤
D.3≤OP≤4
变式演练 如图,P为正比例函数y=x图象上的一个动点,☉P的半径为3,设点P的坐标为(x,y).
(1)求☉P与直线x=2相切时点P的坐标.
(2)请直接写出☉P与直线x=2相交、相离时x的取值范围.
解:(1)过点P作直线x=2的垂线,垂足为A,当点P在直线x=2右侧时,AP=x-2=3,∴x=5,∴P (5, ).当点P在直线x=2的左侧时,PA=2-x=3,∴x=-1,∴P (-1,-) ,∴当☉P与直线x=2相切时,点P的坐标为 (5,) 或 (-1,- ).
(2)当-15时,☉P与直线x=2相离.
九年级·数学·人教版·上册
24.2.2 直线和圆的位置关系
第1课时 直线和圆的三种位置关系
1.知道直线和圆相离、相切、相交的概念、性质和判定方法.
2.探索直线和圆的位置关系,圆心到直线的距离和圆的半径之间的数量关系,并能利用它们解决问题.
◎重点:直线和圆的三种位置关系及其判定方法.
◎难点:直线和圆的三种位置关系的综合应用.
多媒体展示太阳从地平线或海平面升起的情景(或日落时的情况),并从中截取不同的画面,从而引入课题——直线和圆的位置关系.
直线和圆的位置关系
认真阅读课本中本课时的内容,理解“直线和圆的三种位置关系”,尝试独立完成下表.
直线和圆的 位置关系 相 相 相
图形语言
公共点的个数 2 1 0
交
切
离
圆心到直线 l的距离d与 半径r的关系 d r d r d r
公共点的名称
直线的名称
圆心到直线 l的距离d与 半径r的关系 d < r d = r d > r
公共点的名称 交点 切点 无
直线的名称 割线 切线 无
直线和圆的位置关系的判断
1.已知Rt△ABC的斜边AB=6 cm,直角边AC=3 cm.
(1)以C为圆心,以2 cm长为半径的圆和AB的位置关系是 ;
(2)以C为圆心,以4 cm长为半径的圆和AB的位置关系是 ;
相离
相交
(3)以C为圆心,以 cm长为半径的圆和AB的位置关系是相切.
方法归纳交流 判断直线与圆的位置关系的方法:当无法确定直线和圆有几个公共点时,通常过圆心作直线的垂线,计算
的长度,再比较垂线段的长与半径的大小关系即可.
垂线段
变式演练 已知☉O的半径为2,直线l上有一点P满足PO=2,则直线l与☉O的位置关系是( )
A.相切 B.相离
C.相离或相切 D.相切或相交
D
直线和圆的位置关系中的动态问题
2.
如图,在直角坐标系中,☉A的半径为2,圆心坐标为(4,0),y轴上有点B(0,3),点C是☉A上的动点,点P是BC的中点,则OP的范围是( )
A
A.≤OP≤
B.2≤OP≤4
C.≤OP≤
D.3≤OP≤4
变式演练 如图,P为正比例函数y=x图象上的一个动点,☉P的半径为3,设点P的坐标为(x,y).
(1)求☉P与直线x=2相切时点P的坐标.
(2)请直接写出☉P与直线x=2相交、相离时x的取值范围.
解:(1)过点P作直线x=2的垂线,垂足为A,当点P在直线x=2右侧时,AP=x-2=3,∴x=5,∴P (5, ).当点P在直线x=2的左侧时,PA=2-x=3,∴x=-1,∴P (-1,-) ,∴当☉P与直线x=2相切时,点P的坐标为 (5,) 或 (-1,- ).
(2)当-1
同课章节目录
