24.1.4 第1课时 圆周角定理课件(共25张PPT)2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 24.1.4 第1课时 圆周角定理课件(共25张PPT)2023-2024学年人教版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 596.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 23:24:25 | ||
图片预览








文档简介
(共25张PPT)
九年级·数学·人教版·上册
24.1.4 圆周角
第1课时 圆周角定理
1.知道圆周角的概念,能分清圆周角和圆心角.
2.能说出圆周角定理及其推论,并会熟练地运用它们解决问题.
◎重点:圆周角定理及其推论以及它们的应用.
◎难点:当圆心不在圆周角一边上时,圆周角定理的证明.
我们已经学习了圆内一类非常重要的角——圆心角,那么圆内除圆心角外,还有没有其他类型的角呢 如果有,这类角与圆心角又有怎样的关系呢
圆周角的概念
认真阅读课本本课时第1自然段,解决下面的问题.
揭示概念:顶点在 ,并且两边都与圆 ,这样的角叫做圆周角.
圆上
相交
归纳总结 圆心角的顶点在 ,圆周角的顶点在 .一条弧所对的圆心角有 个,一条弧所对的圆周角有 个.
圆心
圆上
一
无数
圆周角定理
认真阅读课本本课时的第二段到“圆周角定理”前一个自然段,认识推出符号“ ”,解决下面的问题.
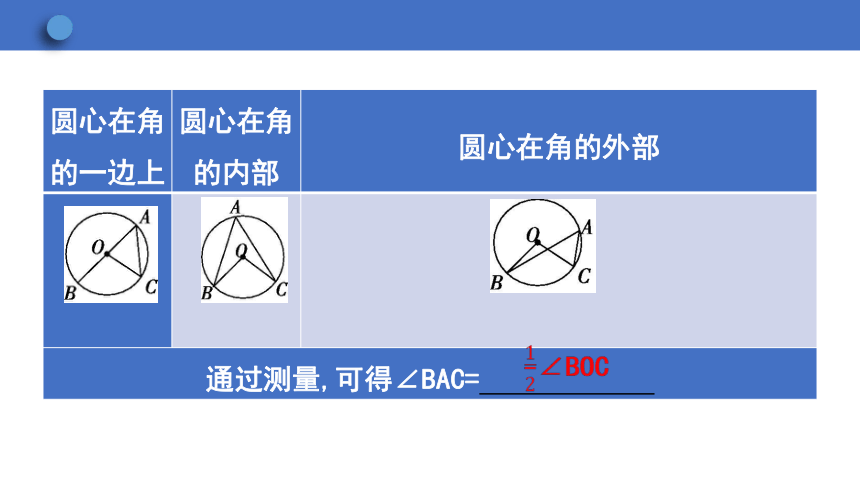
1.圆周角与圆心的位置有以下几种关系,试测量各图中∠BOC与∠BAC的关系.
圆心在角的一边上 圆心在角的内部 圆心在角的外部
通过测量,可得∠BAC=
∠BOC
2.如图,当圆心O在∠BAC内部时,请说明∠A=∠BOC.
解:如图,连接AO并延长交☉O于点D.
∵OA=OB,OA=OC,
∴∠B=∠3,∠C=∠4.
∵∠1=∠B+∠3,∠2=∠C+∠4,
∴∠1=2∠3,∠2=2∠4,
∴∠BOC=∠1+∠2=2∠3+2∠4
=2(∠3+∠4)=2∠BAC,
即∠BAC=∠BOC.
3.如图,当圆心O在∠BAC外部时,请说明∠A=∠BOC.
解:如图,连接AO并延长交☉O于点D.
∵OA=OB,OA=OC,∴∠B=∠1,∠C=∠OAC.
∵∠COD=∠OAC+∠C,∠2=∠1+∠B,
∴∠COD=2∠OAC,∠2=2∠1,
∴∠BOC=∠COD-∠2=2∠OAC-2∠1=2(∠OAC-∠1)=2∠BAC,
即∠BAC=∠BOC.
归纳总结 圆周角定理:一条弧所对的圆周角等于它所对的圆心角的 .
一半
圆周角定理的推论
1.(1)如图,在☉O中,=,则∠MDN与∠ACB的大小关系是 .
(2)直径所对的圆周角是多少度 请说明理由.
(3)90°的圆周角所对的弦是直径吗 请说明理由.
解:(1)∠MDN=∠ACB.
(2)因为直径所对的圆心角是180°,所以直径所对的圆周角是90°.(3)90°圆周角所对的弧是半圆,所以90°圆周角所对的弦是直径.
归纳总结 推论:同弧或等弧所对的圆周角 .半圆(或直径)所对的圆周角是 , 的圆周角所对的弦是直径.
温馨提示 求解有关圆周角(或圆心角)问题的方法:找出或构造出同弧所对的圆心角(或圆周角),根据 定理进行求解.
相等
直角
90°
圆周角
变式演练 如图,BC为☉O的直径,AD⊥BC于点D,P是劣弧AC上一动点,连接PB分别交AD,AC于点E,F.
(1)当AP=AB时,求证:AE=BE.
(2)当点P在什么位置时,AF=EF,证明你的结论.
解:(1)证明:如图,连接AB,AP.
∵AP=AB,∴∠ABP=∠P.
∵BC为☉O直径,
∴∠BAC=90°.
又AD⊥BC,可证∠BAE=∠C.
∵∠C=∠P,∴∠BAE=∠P,
∴∠ABE=∠BAE,∴AE=BE.
(2)当点P在使=的位置时,有AF=EF.
证明:∵=,∴∠EBD=∠C.
∵∠FAE=90°-∠C,∠AEF=∠BED=90°-∠EBD,
∴∠FAE=∠AEF,AF=EF.
圆周角定理、推论的应用
认真阅读课本“例4”,体会圆周角定理、推论的应用,解决下面的问题.
2.如图,在☉O中,弦AB=3 cm,点C在☉O上,∠ACB=30°.求☉O的直径.
解:方法一:如图1,连接OA,OB.
∵∠ACB=30°,
∴∠AOB=60°.
∵OA=OB,
∴△AOB是等边三角形,
∴OA=AB=3 cm,即圆的直径为6 cm.
方法二:如图2,连接AO并延长交☉O于点D,连接BD.
∵AD是直径,
∴∠ABD=90°.
∵∠D=∠C=30°,
∴AD=2AB=6 cm.
变式演练 如图,AB是☉O的直径,BD是☉O的弦,延长BD到点C,使AC=AB,BD与CD的大小有什么关系 为什么
解:BD=CD.
理由:如图,连接AD,∵AB是☉O的直径,
∴∠ADB=90°,即AD⊥BC.
又∵AC=AB,∴BD=CD.
方法归纳交流 一般地,如果题目中有直径出现时,常作辅助线得到直径所对的圆周角—— .当圆中要证明垂直或得到90°的角时,常作出 .
直角
直径
九年级·数学·人教版·上册
24.1.4 圆周角
第1课时 圆周角定理
1.知道圆周角的概念,能分清圆周角和圆心角.
2.能说出圆周角定理及其推论,并会熟练地运用它们解决问题.
◎重点:圆周角定理及其推论以及它们的应用.
◎难点:当圆心不在圆周角一边上时,圆周角定理的证明.
我们已经学习了圆内一类非常重要的角——圆心角,那么圆内除圆心角外,还有没有其他类型的角呢 如果有,这类角与圆心角又有怎样的关系呢
圆周角的概念
认真阅读课本本课时第1自然段,解决下面的问题.
揭示概念:顶点在 ,并且两边都与圆 ,这样的角叫做圆周角.
圆上
相交
归纳总结 圆心角的顶点在 ,圆周角的顶点在 .一条弧所对的圆心角有 个,一条弧所对的圆周角有 个.
圆心
圆上
一
无数
圆周角定理
认真阅读课本本课时的第二段到“圆周角定理”前一个自然段,认识推出符号“ ”,解决下面的问题.
1.圆周角与圆心的位置有以下几种关系,试测量各图中∠BOC与∠BAC的关系.
圆心在角的一边上 圆心在角的内部 圆心在角的外部
通过测量,可得∠BAC=
∠BOC
2.如图,当圆心O在∠BAC内部时,请说明∠A=∠BOC.
解:如图,连接AO并延长交☉O于点D.
∵OA=OB,OA=OC,
∴∠B=∠3,∠C=∠4.
∵∠1=∠B+∠3,∠2=∠C+∠4,
∴∠1=2∠3,∠2=2∠4,
∴∠BOC=∠1+∠2=2∠3+2∠4
=2(∠3+∠4)=2∠BAC,
即∠BAC=∠BOC.
3.如图,当圆心O在∠BAC外部时,请说明∠A=∠BOC.
解:如图,连接AO并延长交☉O于点D.
∵OA=OB,OA=OC,∴∠B=∠1,∠C=∠OAC.
∵∠COD=∠OAC+∠C,∠2=∠1+∠B,
∴∠COD=2∠OAC,∠2=2∠1,
∴∠BOC=∠COD-∠2=2∠OAC-2∠1=2(∠OAC-∠1)=2∠BAC,
即∠BAC=∠BOC.
归纳总结 圆周角定理:一条弧所对的圆周角等于它所对的圆心角的 .
一半
圆周角定理的推论
1.(1)如图,在☉O中,=,则∠MDN与∠ACB的大小关系是 .
(2)直径所对的圆周角是多少度 请说明理由.
(3)90°的圆周角所对的弦是直径吗 请说明理由.
解:(1)∠MDN=∠ACB.
(2)因为直径所对的圆心角是180°,所以直径所对的圆周角是90°.(3)90°圆周角所对的弧是半圆,所以90°圆周角所对的弦是直径.
归纳总结 推论:同弧或等弧所对的圆周角 .半圆(或直径)所对的圆周角是 , 的圆周角所对的弦是直径.
温馨提示 求解有关圆周角(或圆心角)问题的方法:找出或构造出同弧所对的圆心角(或圆周角),根据 定理进行求解.
相等
直角
90°
圆周角
变式演练 如图,BC为☉O的直径,AD⊥BC于点D,P是劣弧AC上一动点,连接PB分别交AD,AC于点E,F.
(1)当AP=AB时,求证:AE=BE.
(2)当点P在什么位置时,AF=EF,证明你的结论.
解:(1)证明:如图,连接AB,AP.
∵AP=AB,∴∠ABP=∠P.
∵BC为☉O直径,
∴∠BAC=90°.
又AD⊥BC,可证∠BAE=∠C.
∵∠C=∠P,∴∠BAE=∠P,
∴∠ABE=∠BAE,∴AE=BE.
(2)当点P在使=的位置时,有AF=EF.
证明:∵=,∴∠EBD=∠C.
∵∠FAE=90°-∠C,∠AEF=∠BED=90°-∠EBD,
∴∠FAE=∠AEF,AF=EF.
圆周角定理、推论的应用
认真阅读课本“例4”,体会圆周角定理、推论的应用,解决下面的问题.
2.如图,在☉O中,弦AB=3 cm,点C在☉O上,∠ACB=30°.求☉O的直径.
解:方法一:如图1,连接OA,OB.
∵∠ACB=30°,
∴∠AOB=60°.
∵OA=OB,
∴△AOB是等边三角形,
∴OA=AB=3 cm,即圆的直径为6 cm.
方法二:如图2,连接AO并延长交☉O于点D,连接BD.
∵AD是直径,
∴∠ABD=90°.
∵∠D=∠C=30°,
∴AD=2AB=6 cm.
变式演练 如图,AB是☉O的直径,BD是☉O的弦,延长BD到点C,使AC=AB,BD与CD的大小有什么关系 为什么
解:BD=CD.
理由:如图,连接AD,∵AB是☉O的直径,
∴∠ADB=90°,即AD⊥BC.
又∵AC=AB,∴BD=CD.
方法归纳交流 一般地,如果题目中有直径出现时,常作辅助线得到直径所对的圆周角—— .当圆中要证明垂直或得到90°的角时,常作出 .
直角
直径
同课章节目录
