24.4 第2课时 圆锥的侧面展开图 课件(共18张PPT) 2023—2024学年人教版数学九年级上册
文档属性
| 名称 | 24.4 第2课时 圆锥的侧面展开图 课件(共18张PPT) 2023—2024学年人教版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 498.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 23:25:12 | ||
图片预览






文档简介
(共18张PPT)
九年级·数学·人教版·上册
24.4 弧长和扇形面积
第2课时 圆锥的侧面展开图
1.知道圆锥母线的概念,知道圆锥的侧面积和全面积公式.
2.会计算圆锥的侧面积和全面积,并能灵活解决有关圆锥的计算题.
◎重点:圆锥侧面积的计算.
◎难点:圆锥侧面展开图的弧长、半径与圆锥底面圆周长、母线长之间的对应关系.
前面我们学习了关于圆和一些多边形的知识,这些图形都属于平面图形,今天我们要研究的是一种立体图形——圆锥.圆锥与我们前面所学面图形有怎样的关系呢 我们应该如何研究圆锥呢
圆锥的有关概念
认真阅读课本本课时“思考”之前的一个自然段,重点理解圆锥的“母线”的概念,填空:
归纳总结 圆锥有 个底面和 个侧面.连接圆锥
和底面圆周上任意一点的 叫做圆锥的母线,所以圆锥有 条母线,这些母线长都 .
一
一
顶点
线段
无数
相等
圆锥侧面积和全面积
认真阅读课本本课时“例3”上面的一个自然段,填空:
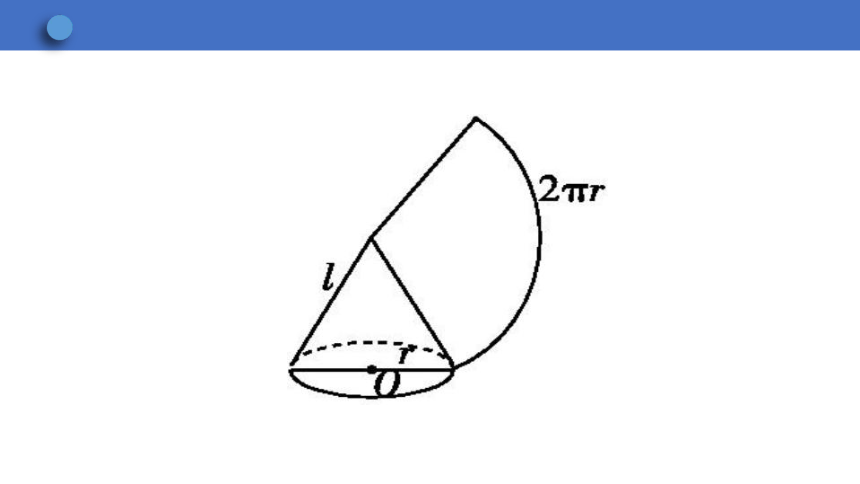
如图,沿圆锥的任意一条母线将圆锥的侧面剪开,得到的是一个 ,它的半径等于圆锥的 长,弧长等于圆锥底面圆的 ,圆锥的侧面积等于 的面积,圆锥的全面积= 面积+ 面积.
扇形
母线
周长
扇形
侧
底
归纳总结 设圆锥的母线长为l,底面圆的半径为r,那么圆锥侧面展开图的扇形的半径为 ,扇形的弧长为 ,圆锥的侧面积为 ,圆锥的全面积为 .
l
2πr
πrl
πrl+πr2
求圆锥侧面展开图的圆心角的度数
1.将一个底面半径为6 cm,母线长为15 cm的圆锥形纸筒沿一条母线剪开,求所得的侧面展开图的圆心角.
解:设所得的侧面展开图的圆心角为α°,
依题意可得=2×6π ,解得α=144.
变式演练 在半径为50 cm的圆形铁皮上剪去一块扇形铁皮,用剩余部分制作成一个底面直径为80 cm,母线长为50 cm的圆锥形烟囱帽,则剪去的扇形的圆心角是多少度
解:设剩余部分扇形的圆心角为n°.
根据剩余部分扇形的弧长等于圆锥底面圆的周长得=80π,解得n=288,
则剪去的圆心角的度数为360°-288°=72°.
求圆锥的高或底面半径
2.如图,已知扇形的圆心角为120°,面积为300π cm2.
(1)求扇形的弧长.
(2)若将此扇形卷成一个圆锥,则这个圆锥底面圆的半径是多少
解:(1)如图, ∵300π=,
∴R=30,∴弧长l==20π(cm).
(2)设底面圆的半径为r.
∵20π=2πr,∴r=10(cm).
综合运用
3.如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过格点A(0,4)、B(-4,4)、C(-6,2),若该圆弧所在圆的圆心为D点,请你利用网格图回答下列问题:
(1)圆心D的坐标为 .
(2)若扇形ADC是一个圆锥的侧面展开图,求该圆锥的底面圆的半径长(结果保留根号).
解:(1)(-2,0).提示:如图1,分别作线段AB和线段BC的垂直平分线,两垂直平分线的交点,就是圆心D, 点D正好在x轴上,点D的坐标是(-2,0).
(2)如图2,连接AC,AD,CD,
易得☉D的半径长==2,AC==2,
∵AD2+CD2=20+20=40,AC2=40,
∴AD2+CD2=AC2,
∴∠ADC=90°.
设圆锥的底面圆的半径长为r,
则2πr=,
解得r=,
所以该圆锥的底面圆的半径长为.
变式演练 已知圆锥的侧面展开图是一个半径为12 cm,弧长为12π cm的扇形,求这个圆锥的侧面积及高.
解:侧面积为×12×12π=72π(cm2).
设底面半径为r,则有2πr=12π,∴r=6 cm.
由于高、母线、底面半径恰好构成直角三角形,根据勾股定理可得高为=6(cm).
九年级·数学·人教版·上册
24.4 弧长和扇形面积
第2课时 圆锥的侧面展开图
1.知道圆锥母线的概念,知道圆锥的侧面积和全面积公式.
2.会计算圆锥的侧面积和全面积,并能灵活解决有关圆锥的计算题.
◎重点:圆锥侧面积的计算.
◎难点:圆锥侧面展开图的弧长、半径与圆锥底面圆周长、母线长之间的对应关系.
前面我们学习了关于圆和一些多边形的知识,这些图形都属于平面图形,今天我们要研究的是一种立体图形——圆锥.圆锥与我们前面所学面图形有怎样的关系呢 我们应该如何研究圆锥呢
圆锥的有关概念
认真阅读课本本课时“思考”之前的一个自然段,重点理解圆锥的“母线”的概念,填空:
归纳总结 圆锥有 个底面和 个侧面.连接圆锥
和底面圆周上任意一点的 叫做圆锥的母线,所以圆锥有 条母线,这些母线长都 .
一
一
顶点
线段
无数
相等
圆锥侧面积和全面积
认真阅读课本本课时“例3”上面的一个自然段,填空:
如图,沿圆锥的任意一条母线将圆锥的侧面剪开,得到的是一个 ,它的半径等于圆锥的 长,弧长等于圆锥底面圆的 ,圆锥的侧面积等于 的面积,圆锥的全面积= 面积+ 面积.
扇形
母线
周长
扇形
侧
底
归纳总结 设圆锥的母线长为l,底面圆的半径为r,那么圆锥侧面展开图的扇形的半径为 ,扇形的弧长为 ,圆锥的侧面积为 ,圆锥的全面积为 .
l
2πr
πrl
πrl+πr2
求圆锥侧面展开图的圆心角的度数
1.将一个底面半径为6 cm,母线长为15 cm的圆锥形纸筒沿一条母线剪开,求所得的侧面展开图的圆心角.
解:设所得的侧面展开图的圆心角为α°,
依题意可得=2×6π ,解得α=144.
变式演练 在半径为50 cm的圆形铁皮上剪去一块扇形铁皮,用剩余部分制作成一个底面直径为80 cm,母线长为50 cm的圆锥形烟囱帽,则剪去的扇形的圆心角是多少度
解:设剩余部分扇形的圆心角为n°.
根据剩余部分扇形的弧长等于圆锥底面圆的周长得=80π,解得n=288,
则剪去的圆心角的度数为360°-288°=72°.
求圆锥的高或底面半径
2.如图,已知扇形的圆心角为120°,面积为300π cm2.
(1)求扇形的弧长.
(2)若将此扇形卷成一个圆锥,则这个圆锥底面圆的半径是多少
解:(1)如图, ∵300π=,
∴R=30,∴弧长l==20π(cm).
(2)设底面圆的半径为r.
∵20π=2πr,∴r=10(cm).
综合运用
3.如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过格点A(0,4)、B(-4,4)、C(-6,2),若该圆弧所在圆的圆心为D点,请你利用网格图回答下列问题:
(1)圆心D的坐标为 .
(2)若扇形ADC是一个圆锥的侧面展开图,求该圆锥的底面圆的半径长(结果保留根号).
解:(1)(-2,0).提示:如图1,分别作线段AB和线段BC的垂直平分线,两垂直平分线的交点,就是圆心D, 点D正好在x轴上,点D的坐标是(-2,0).
(2)如图2,连接AC,AD,CD,
易得☉D的半径长==2,AC==2,
∵AD2+CD2=20+20=40,AC2=40,
∴AD2+CD2=AC2,
∴∠ADC=90°.
设圆锥的底面圆的半径长为r,
则2πr=,
解得r=,
所以该圆锥的底面圆的半径长为.
变式演练 已知圆锥的侧面展开图是一个半径为12 cm,弧长为12π cm的扇形,求这个圆锥的侧面积及高.
解:侧面积为×12×12π=72π(cm2).
设底面半径为r,则有2πr=12π,∴r=6 cm.
由于高、母线、底面半径恰好构成直角三角形,根据勾股定理可得高为=6(cm).
同课章节目录
