23.2.3 关于原点对称的点的坐标 课件 (共16张PPT)2023—2024学年人教版数学九年级上册
文档属性
| 名称 | 23.2.3 关于原点对称的点的坐标 课件 (共16张PPT)2023—2024学年人教版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 368.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
九年级·数学·人教版·上册
23.2.3 关于原点对称的点的坐标
23.2.3 关于原点对称的点的坐标
1.能运用中心对称的知识猜想并验证关于原点对称的点的坐标的特点.
2.会在平面直角坐标系中作关于原点对称的图形,养成观察、分析、探究及合作交流的学习习惯.
◎重点:平面直角坐标系中关于原点对称的点的坐标的特点及其应用.
◎难点:平面直角坐标系中关于原点对称的点的坐标的特点及其应用.
在学习轴对称的知识时,我们学习了坐标系内关于坐标轴对称的点的坐标变化规律,那么在坐标系内,关于原点对称的点的坐标有什么特点呢
关于原点对称的点的坐标
阅读课本本课时“探究”及“归纳”的内容,解决下列问题.
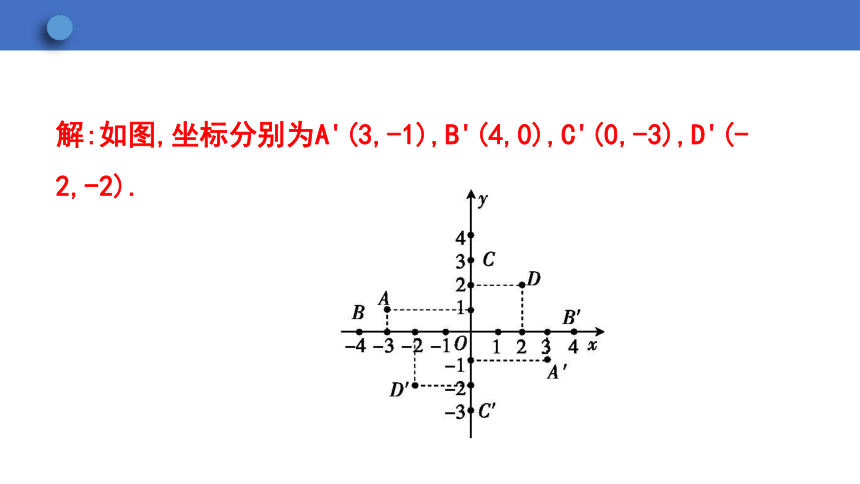
1.如图,在直角坐标系中,已知A(-3,1),B(-4,0),C(0,3),D(2,2),分别作出A,B,C,D点关于原点O的对称点,并写出它们的坐标.
解:如图,坐标分别为A'(3,-1),B'(4,0),C'(0,-3),D'(-2,-2).
2.根据上面的探究,两个点关于原点对称时,①它们的横坐标的绝对值有什么关系 纵坐标的绝对值又有什么关系 ②坐标与坐标之间的符号又有什么特点
答:①它们的横坐标的绝对值相等,纵坐标的绝对值相等;②符号相反.
归纳总结 两个点关于原点对称时,它们的坐标符号 ,即点P(x,y)关于原点的对称点为P'( ).
相反
-x , -y
作关于原点对称的图形
阅读课本本课时“例2”,解决下列问题.
1.在“例2”中,点A、B、C的坐标分别为 、
、 ,这三个点关于原点对称的点的坐标分别为A' ,B' ,C' .
(-4,1)
(-1,-1)
(-3,2)
(4,-1)
(1,1)
(3,-2)
2.依次连接A'B',B'C',C'A',得到的 即为所求作的三角形.
归纳总结 在平面直角坐标系中作关于原点对称的图形的步骤:(1)找出图形中的 (如线段的端点,角的顶点等);(2)写出各关键点关于 对称的点的 ;(3)在坐标平面内描出这些对称点;(4)顺次 即为所求作的对称图形.
△A'B'C'
关键点
原点
坐标
连接各点
关于原点对称的点的坐标
1.写出下列已知点关于原点O对称的点的坐标.
A(3,0),B(0,-2),C(-1,4),D(-3,-2),E(2,3).
解:A'(-3,0),B'(0,2),C'(1,-4),D'(3,2),E'(-2,-3).
变式演练 若点P(a+1,a-2)关于原点对称的点位于第二象限,则a的取值范围表示正确的是 ( )
A B
C D
C
作关于原点对称的图形
2.△ABC在如图所示的平面直角坐标系中.
(1)画出△ABC关于y轴对称的△A1B1C1.
(2)画出△ABC关于原点对称的△A2B2C2.
(3)试判断△A1B1C1与△A2B2C2的关系.
解:(1)(2)如图所示.(3)关于x轴对称.
变式演练
如图,在平面直角坐标系中,A(-3,1),B(-2,3),C(0,2),画出△ABC 关于y轴对称的△A'B'C',再画出△A'B'C'关于x轴对称的△A″B″C″,那么△A″B″C″与△ABC有什么关系 请说明理由.
解:△A″B″C″与△ABC关于原点对称.
理由:∵A″(3,-1),B″(2,-3),C″(0,-2),
∴A点与A″点,B点与B″点,C点与C″点关于原点O对称,
∴△A″B″C″与△ABC关于原点对称.
九年级·数学·人教版·上册
23.2.3 关于原点对称的点的坐标
23.2.3 关于原点对称的点的坐标
1.能运用中心对称的知识猜想并验证关于原点对称的点的坐标的特点.
2.会在平面直角坐标系中作关于原点对称的图形,养成观察、分析、探究及合作交流的学习习惯.
◎重点:平面直角坐标系中关于原点对称的点的坐标的特点及其应用.
◎难点:平面直角坐标系中关于原点对称的点的坐标的特点及其应用.
在学习轴对称的知识时,我们学习了坐标系内关于坐标轴对称的点的坐标变化规律,那么在坐标系内,关于原点对称的点的坐标有什么特点呢
关于原点对称的点的坐标
阅读课本本课时“探究”及“归纳”的内容,解决下列问题.
1.如图,在直角坐标系中,已知A(-3,1),B(-4,0),C(0,3),D(2,2),分别作出A,B,C,D点关于原点O的对称点,并写出它们的坐标.
解:如图,坐标分别为A'(3,-1),B'(4,0),C'(0,-3),D'(-2,-2).
2.根据上面的探究,两个点关于原点对称时,①它们的横坐标的绝对值有什么关系 纵坐标的绝对值又有什么关系 ②坐标与坐标之间的符号又有什么特点
答:①它们的横坐标的绝对值相等,纵坐标的绝对值相等;②符号相反.
归纳总结 两个点关于原点对称时,它们的坐标符号 ,即点P(x,y)关于原点的对称点为P'( ).
相反
-x , -y
作关于原点对称的图形
阅读课本本课时“例2”,解决下列问题.
1.在“例2”中,点A、B、C的坐标分别为 、
、 ,这三个点关于原点对称的点的坐标分别为A' ,B' ,C' .
(-4,1)
(-1,-1)
(-3,2)
(4,-1)
(1,1)
(3,-2)
2.依次连接A'B',B'C',C'A',得到的 即为所求作的三角形.
归纳总结 在平面直角坐标系中作关于原点对称的图形的步骤:(1)找出图形中的 (如线段的端点,角的顶点等);(2)写出各关键点关于 对称的点的 ;(3)在坐标平面内描出这些对称点;(4)顺次 即为所求作的对称图形.
△A'B'C'
关键点
原点
坐标
连接各点
关于原点对称的点的坐标
1.写出下列已知点关于原点O对称的点的坐标.
A(3,0),B(0,-2),C(-1,4),D(-3,-2),E(2,3).
解:A'(-3,0),B'(0,2),C'(1,-4),D'(3,2),E'(-2,-3).
变式演练 若点P(a+1,a-2)关于原点对称的点位于第二象限,则a的取值范围表示正确的是 ( )
A B
C D
C
作关于原点对称的图形
2.△ABC在如图所示的平面直角坐标系中.
(1)画出△ABC关于y轴对称的△A1B1C1.
(2)画出△ABC关于原点对称的△A2B2C2.
(3)试判断△A1B1C1与△A2B2C2的关系.
解:(1)(2)如图所示.(3)关于x轴对称.
变式演练
如图,在平面直角坐标系中,A(-3,1),B(-2,3),C(0,2),画出△ABC 关于y轴对称的△A'B'C',再画出△A'B'C'关于x轴对称的△A″B″C″,那么△A″B″C″与△ABC有什么关系 请说明理由.
解:△A″B″C″与△ABC关于原点对称.
理由:∵A″(3,-1),B″(2,-3),C″(0,-2),
∴A点与A″点,B点与B″点,C点与C″点关于原点O对称,
∴△A″B″C″与△ABC关于原点对称.
同课章节目录
