等腰三角形判定(浙江省台州市仙居县)
文档属性
| 名称 | 等腰三角形判定(浙江省台州市仙居县) |  | |
| 格式 | rar | ||
| 文件大小 | 404.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-09-27 19:54:00 | ||
图片预览



文档简介
课件27张PPT。第十四章 轴对称等腰三角形2仙居外语学校 李志成等腰三角形有些什么性质?1.等腰三角形的两底角相等.
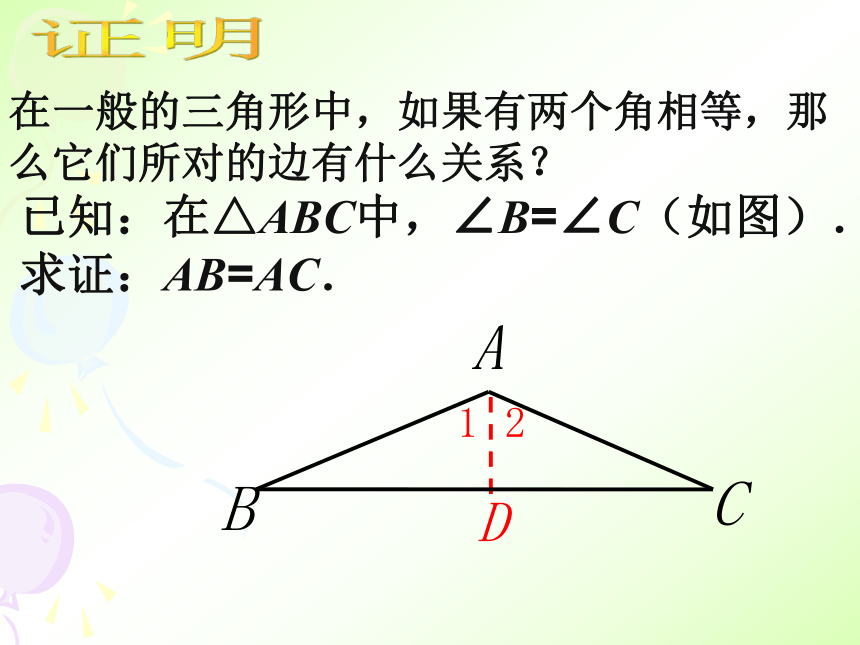
(简写成 “等边对等角”) 复习∵AB=AC(已知)
∴∠B=∠C(等边对等角)CDBA①在ΔABC中,∵AB=AC,
∴ ∠B=∠C( )等边对等角(1)∵AD⊥BC,
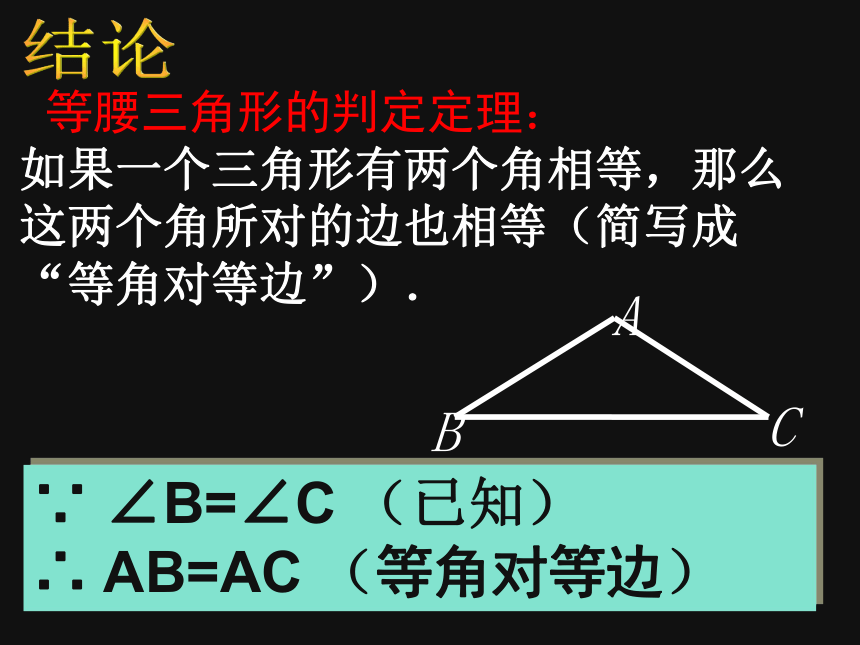
∴∠____ = ∠____,___= ___ (2)∵AD是中线,∴___⊥___ ,∠____ =∠____ (3)∵AD是角平分线,∴___ ⊥___ ,___ =___BAD CADBD CD AD BC AD BCBAD CADBD CD②在△ABC中, AB=AC时, 等腰三角形底边上的中线和高线、顶角的平分线互相重合。O如图,位于在海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?探究AB在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?已知:在△ABC中,∠B=∠C(如图).
求证:AB=AC.证明 等腰三角形的判定定理:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”). 结论∵ ∠B=∠C (已知)
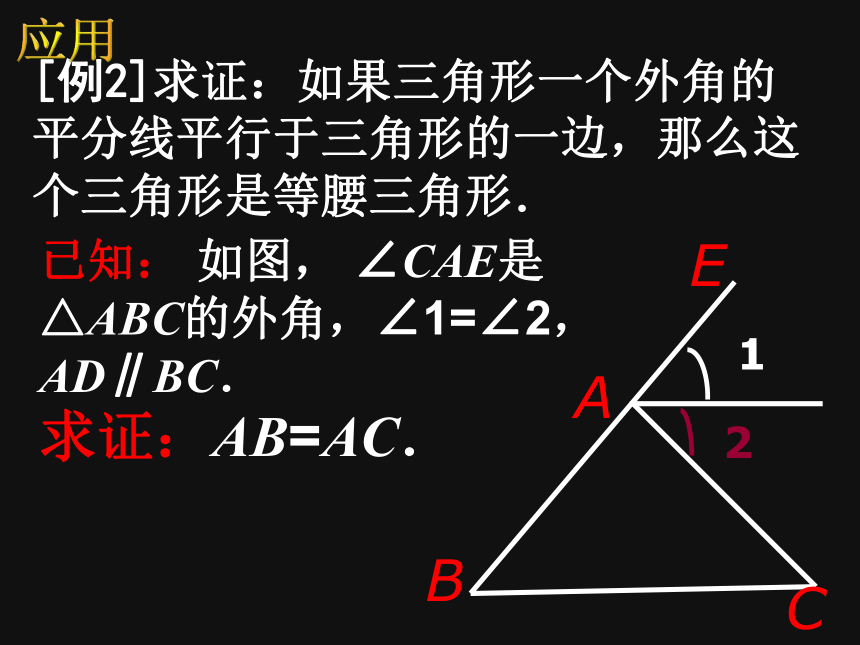
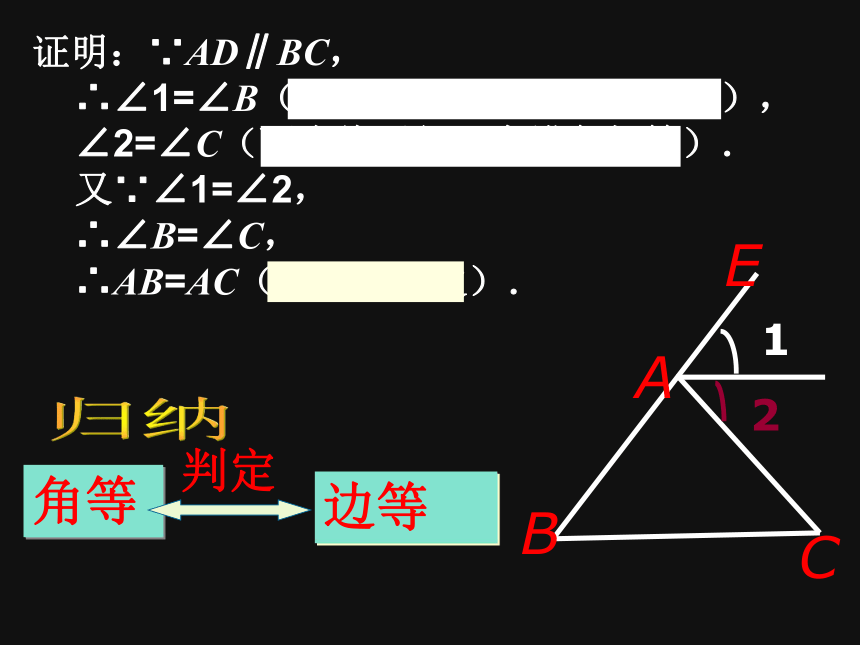
∴ AB=AC (等角对等边)[例2]求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形. 已知: 如图, ∠CAE是△ABC的外角,∠1=∠2,AD∥BC. 求证:AB=AC. 应用证明:∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等),
∠2=∠C(两直线平行,内错角相等).
又∵∠1=∠2,
∴∠B=∠C,
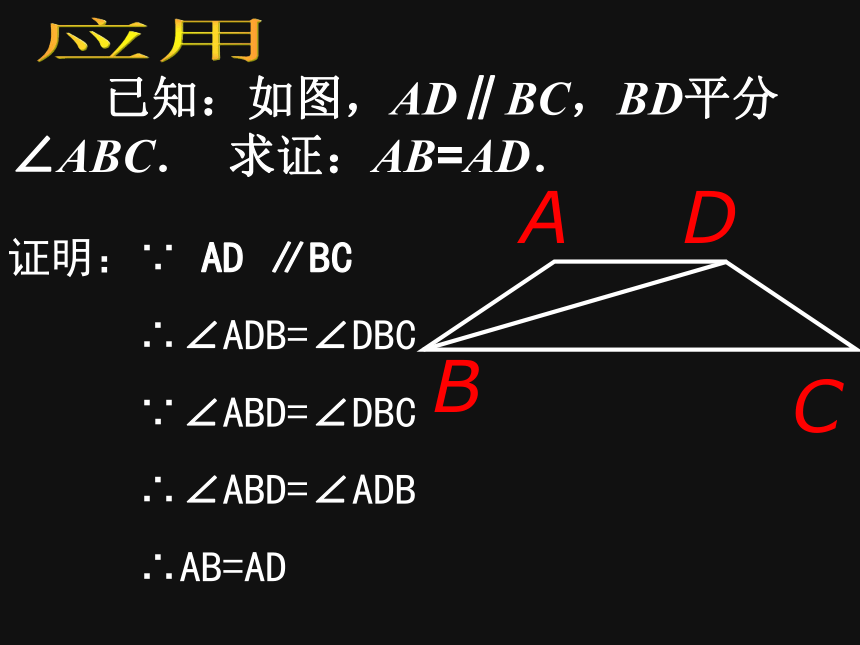
∴AB=AC(等角对等边). 角等边等判定归纳 已知:如图,AD∥BC,BD平分∠ABC. 求证:AB=AD.应用证明:∵ AD ∥BC
∴∠ADB=∠DBC
∵∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD 如图,△ABC中,∠ABC与∠ ACB的平分线交于点D,过点D作EF∥BC交AB于E,交AC于点F,
求证:EF=BE+CF挑战6: 已知:如图,BI平分∠ABC,CI平分∠ACB,DE经过点I,且DE∥BC. AB=12, AC=17求△ADE的周长深 入思考:在△ABC中,已知 ,BO平分∠ABC,CO平分∠ACB.(1)请问图中有多少个等腰三角形?说明理由.(2)线段EF和线段EB,FC之间有没有关系?若有是什么关系?AB=ACAB≠ACEF过点O作直线EF//BC交AB于E,交AC于F.ABCoEFAB≠AC 1.如图,∠A=36°∠DBC=36°,∠C=72°,分别计算∠1、∠2的度数,并说明图中有哪些等腰三角形.练习DCBA122.如图,把一张矩形的纸沿对角线折叠.重合部分是一个等腰三角形吗?为什么?练习3.如图,AC和BD相交于点O,且AB∥DC,OA=OB,求证:OC=OD. 练习 请把这个等腰三角形纸片折成两个等腰三角形?36°⌒
ABC探究1(折成3个等腰三角形呢?)请把这个三角形纸片折成两个等腰三角形!探究21、对∠A进行讨论(分类讨论)探究22、对∠B进行讨论3、对∠C进行讨论已知点A的坐标为(1,-1),在y轴上找一点P,使△POA为等腰三角形.这样的点P共有多少个?实验室探究3P1P2P3P4其中,以OA为腰的三角形有△OAP1、 △OAP2、 △OAP3,
以OA为底的三角形有△OAP4如图, △ABC中,AB=AC,D为AB上一点,E为AC延长线上一点,且BD=CE,DE交BC于G.求证:DG=EG.思路
因为△GDB和△GEC不全等,所以考虑在△GDB内作出一个与△GEC全等的三角形。★★思考题: FEDCBA 已知如图AB=AC,BD=CE,∠B=∠C,且点F是DE的中点,判断AF与DE关系?如图C、E和B、D、F、分别在∠GAH两边上,且AB=BC=CD=DE=EF, ∠ A=18°则∠GEF度数是_____如图是一钢架,∠AOB=10°,为使钢架现加坚固,需在内部添加一些钢管EF、FG、GH、 ‥‥ 添加的钢管长度都与OE相等,则最多能添加多少这样的钢管?B内容回顾 本节课你学到了什么? 再 见!
(简写成 “等边对等角”) 复习∵AB=AC(已知)
∴∠B=∠C(等边对等角)CDBA①在ΔABC中,∵AB=AC,
∴ ∠B=∠C( )等边对等角(1)∵AD⊥BC,
∴∠____ = ∠____,___= ___ (2)∵AD是中线,∴___⊥___ ,∠____ =∠____ (3)∵AD是角平分线,∴___ ⊥___ ,___ =___BAD CADBD CD AD BC AD BCBAD CADBD CD②在△ABC中, AB=AC时, 等腰三角形底边上的中线和高线、顶角的平分线互相重合。O如图,位于在海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?探究AB在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?已知:在△ABC中,∠B=∠C(如图).
求证:AB=AC.证明 等腰三角形的判定定理:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”). 结论∵ ∠B=∠C (已知)
∴ AB=AC (等角对等边)[例2]求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形. 已知: 如图, ∠CAE是△ABC的外角,∠1=∠2,AD∥BC. 求证:AB=AC. 应用证明:∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等),
∠2=∠C(两直线平行,内错角相等).
又∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等角对等边). 角等边等判定归纳 已知:如图,AD∥BC,BD平分∠ABC. 求证:AB=AD.应用证明:∵ AD ∥BC
∴∠ADB=∠DBC
∵∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD 如图,△ABC中,∠ABC与∠ ACB的平分线交于点D,过点D作EF∥BC交AB于E,交AC于点F,
求证:EF=BE+CF挑战6: 已知:如图,BI平分∠ABC,CI平分∠ACB,DE经过点I,且DE∥BC. AB=12, AC=17求△ADE的周长深 入思考:在△ABC中,已知 ,BO平分∠ABC,CO平分∠ACB.(1)请问图中有多少个等腰三角形?说明理由.(2)线段EF和线段EB,FC之间有没有关系?若有是什么关系?AB=ACAB≠ACEF过点O作直线EF//BC交AB于E,交AC于F.ABCoEFAB≠AC 1.如图,∠A=36°∠DBC=36°,∠C=72°,分别计算∠1、∠2的度数,并说明图中有哪些等腰三角形.练习DCBA122.如图,把一张矩形的纸沿对角线折叠.重合部分是一个等腰三角形吗?为什么?练习3.如图,AC和BD相交于点O,且AB∥DC,OA=OB,求证:OC=OD. 练习 请把这个等腰三角形纸片折成两个等腰三角形?36°⌒
ABC探究1(折成3个等腰三角形呢?)请把这个三角形纸片折成两个等腰三角形!探究21、对∠A进行讨论(分类讨论)探究22、对∠B进行讨论3、对∠C进行讨论已知点A的坐标为(1,-1),在y轴上找一点P,使△POA为等腰三角形.这样的点P共有多少个?实验室探究3P1P2P3P4其中,以OA为腰的三角形有△OAP1、 △OAP2、 △OAP3,
以OA为底的三角形有△OAP4如图, △ABC中,AB=AC,D为AB上一点,E为AC延长线上一点,且BD=CE,DE交BC于G.求证:DG=EG.思路
因为△GDB和△GEC不全等,所以考虑在△GDB内作出一个与△GEC全等的三角形。★★思考题: FEDCBA 已知如图AB=AC,BD=CE,∠B=∠C,且点F是DE的中点,判断AF与DE关系?如图C、E和B、D、F、分别在∠GAH两边上,且AB=BC=CD=DE=EF, ∠ A=18°则∠GEF度数是_____如图是一钢架,∠AOB=10°,为使钢架现加坚固,需在内部添加一些钢管EF、FG、GH、 ‥‥ 添加的钢管长度都与OE相等,则最多能添加多少这样的钢管?B内容回顾 本节课你学到了什么? 再 见!
