1.3.1单调性与最大(小)值
文档属性
| 名称 | 1.3.1单调性与最大(小)值 |  | |
| 格式 | rar | ||
| 文件大小 | 175.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-09-27 09:43:00 | ||
图片预览

文档简介
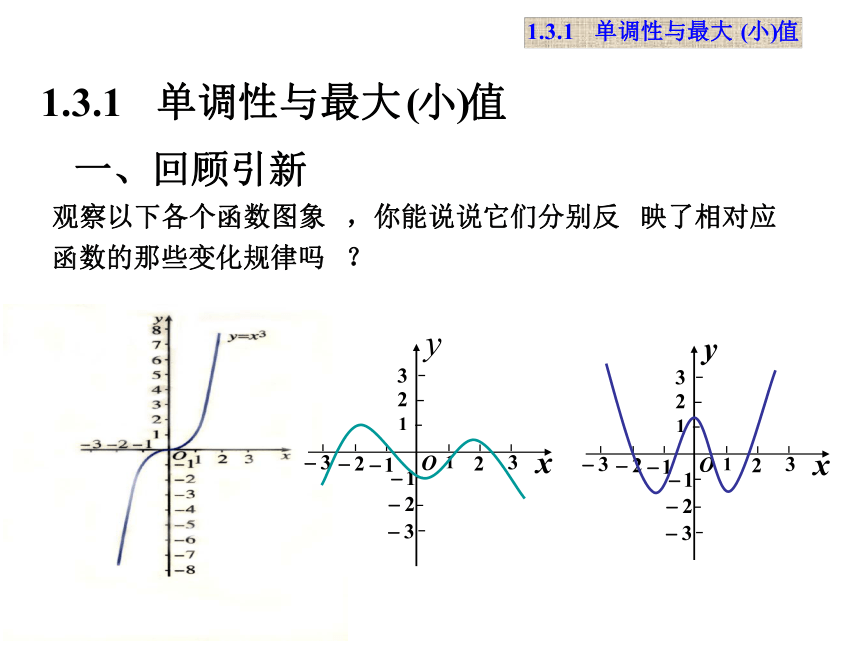
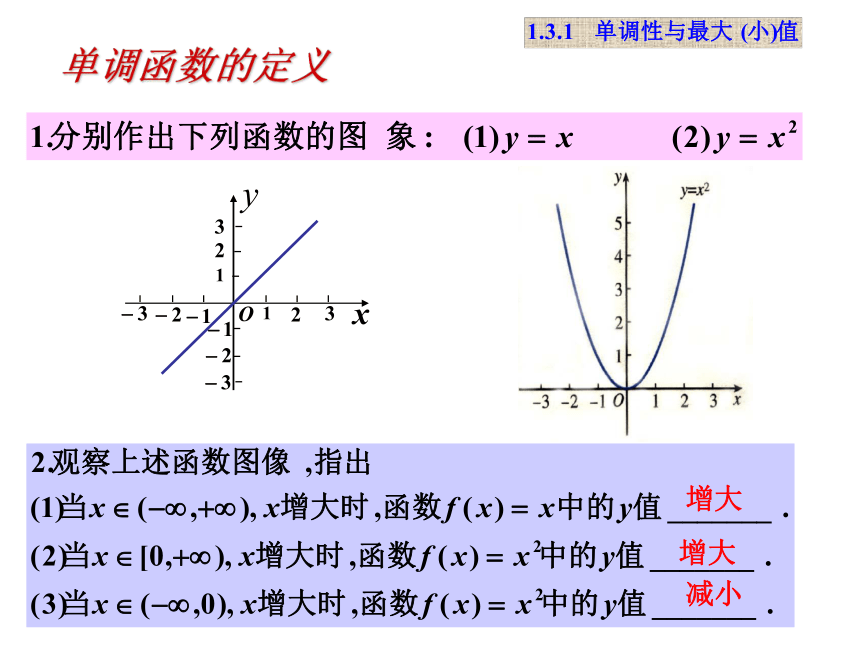
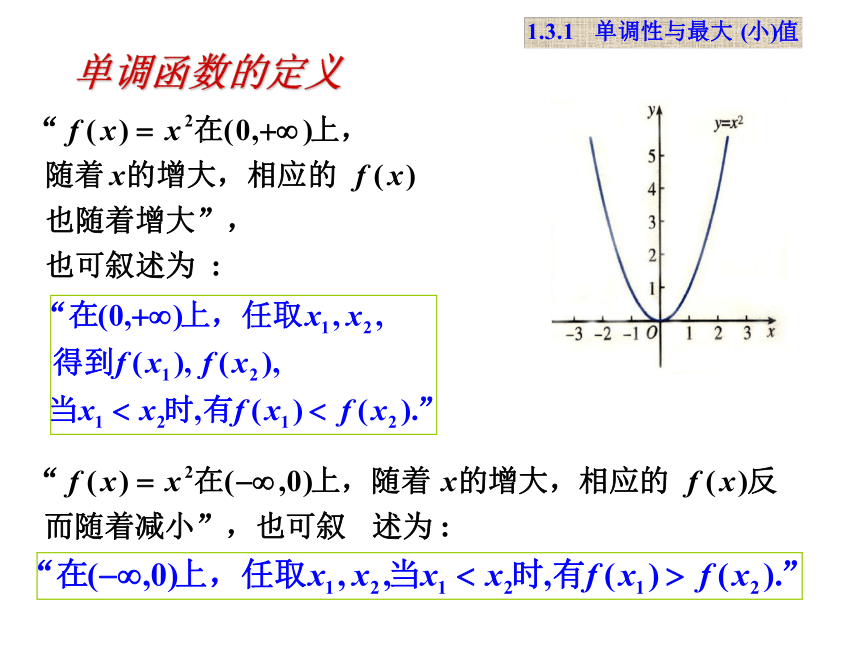
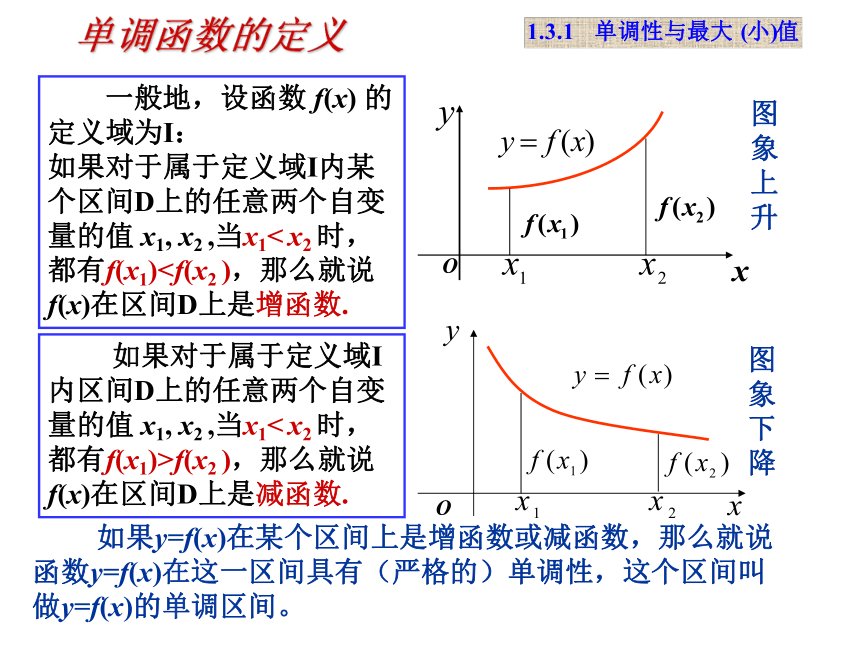
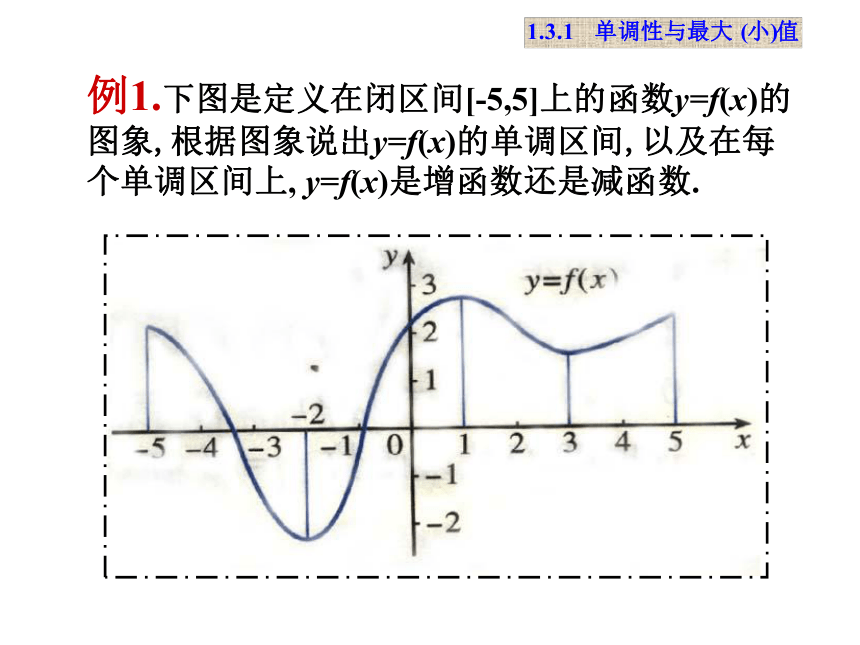
课件13张PPT。 1.3 函数的基本性质第一课时2008年9月16日第一章 集合与函数的概念增大增大减小单调函数的定义单调函数的定义 一般地,设函数 f(x) 的定义域为I: 如果对于属于定义域I内某个区间D上的任意两个自变量的值 x1, x2 ,当x1< x2 时,都有f(x1)f(x2 ),那么就说f(x)在区间D上是减函数.图象下降单调函数的定义 如果y=f(x)在某个区间上是增函数或减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,这个区间叫做y=f(x)的单调区间。图象上升例1.下图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每个单调区间上, y=f(x)是增函数还是减函数.例4、已知函数y=x2-2x+3在区间(-∞,a]上单调递减,则a的取值范围是__.最大值定义:
一般地,设函数 y= f(x) 的定义域为I,如果存在实数M满足: (1)对于任意的 x∈I ,都有 f(x)≤M ;(2)存在x0 ∈I,使得 f(x0 )=M. 那么,我们称M是函数y= f(x)的最大值.仿照上述定义,你能给出函数y=f(x)的最小值的定义吗?最小值定义:
一般地,设函数 y= f(x) 的定义域为I,如果存在实数M满足: (1)对于任意的 x∈I ,都有 f(x) M ;(2)存在x0 ∈I,使得 f(x0 )=M. 那么,我们称M是函数y= f(x)的最小值.最大最小值的意义例5.”菊花”烟花是最壮观的烟花之一.制造时一般是期望在它达到最高点时爆裂.如果烟花距地面的高度 h (m)与时间t(s)之间的关系为 ,那么烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少?(精确到1m)归纳小结对于函数单调性的定义的理解,要注意以下三点:(1)单调性是与“区间”紧密相关的概念.一个函数在不同的区间上可以有不同的单调性.(3)由于定义都是充要性命题,因此由 是增(减)函数,且 ,这说明单调性使得自变量间的不等关系和函数值之间的不等关系可以“正逆互推”。(2)单调性是函数在某一区间上的“整体”性质.因此,定义中的x1, x2 具有任意性,不能用特殊值代替. (4)最大值、最小值的意义
一般地,设函数 y= f(x) 的定义域为I,如果存在实数M满足: (1)对于任意的 x∈I ,都有 f(x)≤M ;(2)存在x0 ∈I,使得 f(x0 )=M. 那么,我们称M是函数y= f(x)的最大值.仿照上述定义,你能给出函数y=f(x)的最小值的定义吗?最小值定义:
一般地,设函数 y= f(x) 的定义域为I,如果存在实数M满足: (1)对于任意的 x∈I ,都有 f(x) M ;(2)存在x0 ∈I,使得 f(x0 )=M. 那么,我们称M是函数y= f(x)的最小值.最大最小值的意义例5.”菊花”烟花是最壮观的烟花之一.制造时一般是期望在它达到最高点时爆裂.如果烟花距地面的高度 h (m)与时间t(s)之间的关系为 ,那么烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少?(精确到1m)归纳小结对于函数单调性的定义的理解,要注意以下三点:(1)单调性是与“区间”紧密相关的概念.一个函数在不同的区间上可以有不同的单调性.(3)由于定义都是充要性命题,因此由 是增(减)函数,且 ,这说明单调性使得自变量间的不等关系和函数值之间的不等关系可以“正逆互推”。(2)单调性是函数在某一区间上的“整体”性质.因此,定义中的x1, x2 具有任意性,不能用特殊值代替. (4)最大值、最小值的意义
