12.1. 线段垂直平分线的性质
文档属性
| 名称 | 12.1. 线段垂直平分线的性质 |

|
|
| 格式 | rar | ||
| 文件大小 | 18.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-09-26 15:16:00 | ||
图片预览

文档简介
学校 班级 姓名 学号
§14.1. 线段垂直平分线的性质(P32--33)
第三课时
学习目标
探究线段垂直平分线的性质.
环节一:
1、 已知线段AB, 画出线段AB的垂直
平分线MN,垂足为C;
2 、在垂直平分线MN上任取一点P,连结PA、
PB;量一量:PA、PB的长,你能发现什么?
环节二:
命题:线段垂直平分线上的点与这条线段两个端点的距离相等。
已知:如图,直线MN⊥AB,垂足为C, 且AC=BC,
在MN上任取一点P.
求证:PA=PB
垂直平分线的性质定理:
线段垂直平分线上的点 相等。
数学推理过程:(如上图)
∵PC垂直平分线段AB (或AC=BC PC⊥AB)
∴PA=PB
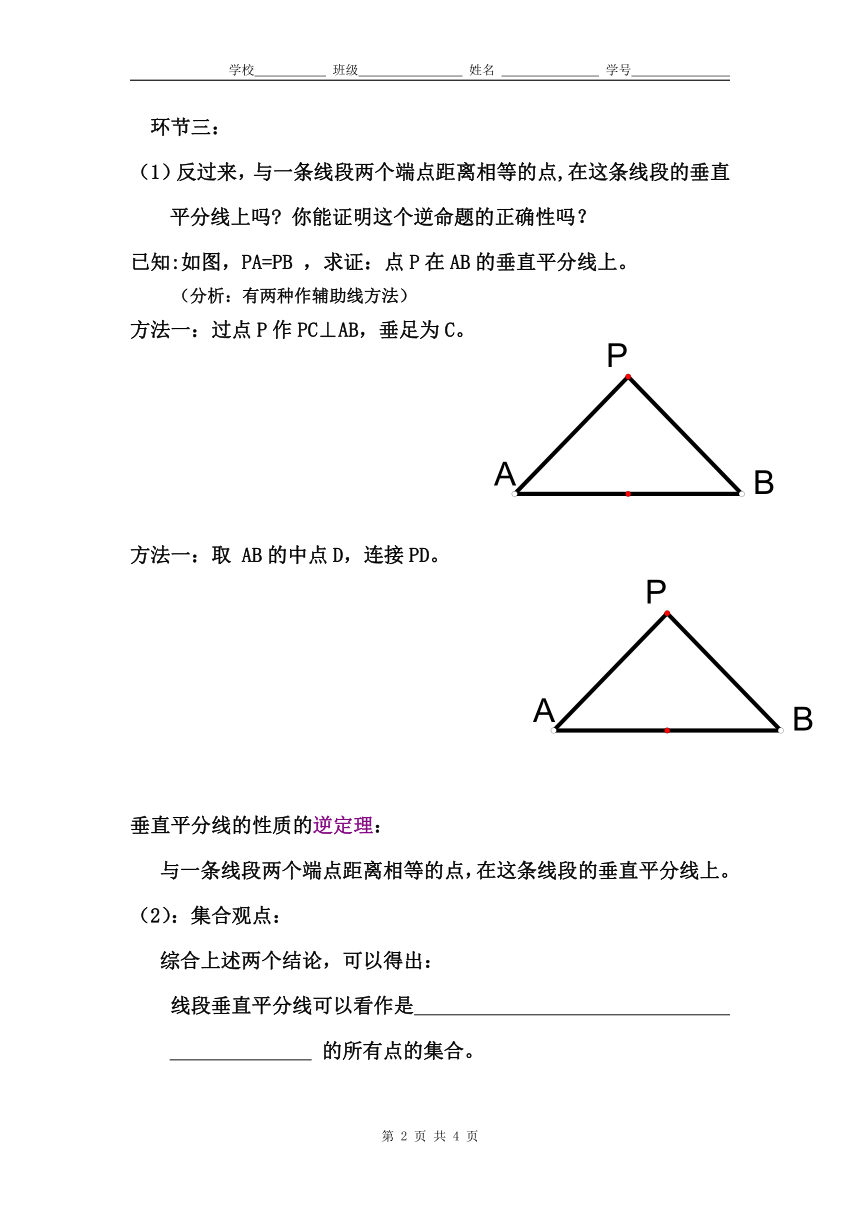
环节三:
(1)反过来,与一条线段两个端点距离相等的点,在这条线段的垂直平分线上吗 你能证明这个逆命题的正确性吗?
已知:如图,PA=PB ,求证:点P在AB的垂直平分线上。
(分析:有两种作辅助线方法)
方法一:过点P作PC⊥AB,垂足为C。
方法一:取 AB的中点D,连接PD。
垂直平分线的性质的逆定理:
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
(2):集合观点:
综合上述两个结论,可以得出:
线段垂直平分线可以看作是
的所有点的集合。
练习:
1.如图,已知,AB=5, AD⊥BC,
BD=DC,则AC= 。
2. 如图,已知点A、点B以及直线L,在直线L上求作一点P,
使PA=PB.
3、 如图,已知AE=CE, BD⊥AC.求证: AD+AB=CD+BC.
环节五:课外作业:
(C.B层)1、如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7cm,那么ED= cm.
(C.B.A层)2、在V型公路(∠AOB)内部,有两个村庄C、D。
你能选择一个纺织厂的厂址P,使P到V型公路的距离相等,
且使C、D两村的工人上下班的路程一样吗?
(B.A层)3.求作一点P,使它和已知△ABC
的三个顶点距离相等.
(A层)4.如图, AD⊥BC,BD=DC,点C在AE的垂直平分线上。
(1)AB,AC,CE的长度有什么关系 为什么
(2) AB+BD与DE有什么关系 为什么
C
D
B
A
C
B
A
D
E
第 3 页 共 4 页
§14.1. 线段垂直平分线的性质(P32--33)
第三课时
学习目标
探究线段垂直平分线的性质.
环节一:
1、 已知线段AB, 画出线段AB的垂直
平分线MN,垂足为C;
2 、在垂直平分线MN上任取一点P,连结PA、
PB;量一量:PA、PB的长,你能发现什么?
环节二:
命题:线段垂直平分线上的点与这条线段两个端点的距离相等。
已知:如图,直线MN⊥AB,垂足为C, 且AC=BC,
在MN上任取一点P.
求证:PA=PB
垂直平分线的性质定理:
线段垂直平分线上的点 相等。
数学推理过程:(如上图)
∵PC垂直平分线段AB (或AC=BC PC⊥AB)
∴PA=PB
环节三:
(1)反过来,与一条线段两个端点距离相等的点,在这条线段的垂直平分线上吗 你能证明这个逆命题的正确性吗?
已知:如图,PA=PB ,求证:点P在AB的垂直平分线上。
(分析:有两种作辅助线方法)
方法一:过点P作PC⊥AB,垂足为C。
方法一:取 AB的中点D,连接PD。
垂直平分线的性质的逆定理:
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
(2):集合观点:
综合上述两个结论,可以得出:
线段垂直平分线可以看作是
的所有点的集合。
练习:
1.如图,已知,AB=5, AD⊥BC,
BD=DC,则AC= 。
2. 如图,已知点A、点B以及直线L,在直线L上求作一点P,
使PA=PB.
3、 如图,已知AE=CE, BD⊥AC.求证: AD+AB=CD+BC.
环节五:课外作业:
(C.B层)1、如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7cm,那么ED= cm.
(C.B.A层)2、在V型公路(∠AOB)内部,有两个村庄C、D。
你能选择一个纺织厂的厂址P,使P到V型公路的距离相等,
且使C、D两村的工人上下班的路程一样吗?
(B.A层)3.求作一点P,使它和已知△ABC
的三个顶点距离相等.
(A层)4.如图, AD⊥BC,BD=DC,点C在AE的垂直平分线上。
(1)AB,AC,CE的长度有什么关系 为什么
(2) AB+BD与DE有什么关系 为什么
C
D
B
A
C
B
A
D
E
第 3 页 共 4 页
