17.1一元二次方程 课件(共23张PPT)
文档属性
| 名称 | 17.1一元二次方程 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 278.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-03 00:00:00 | ||
图片预览






文档简介
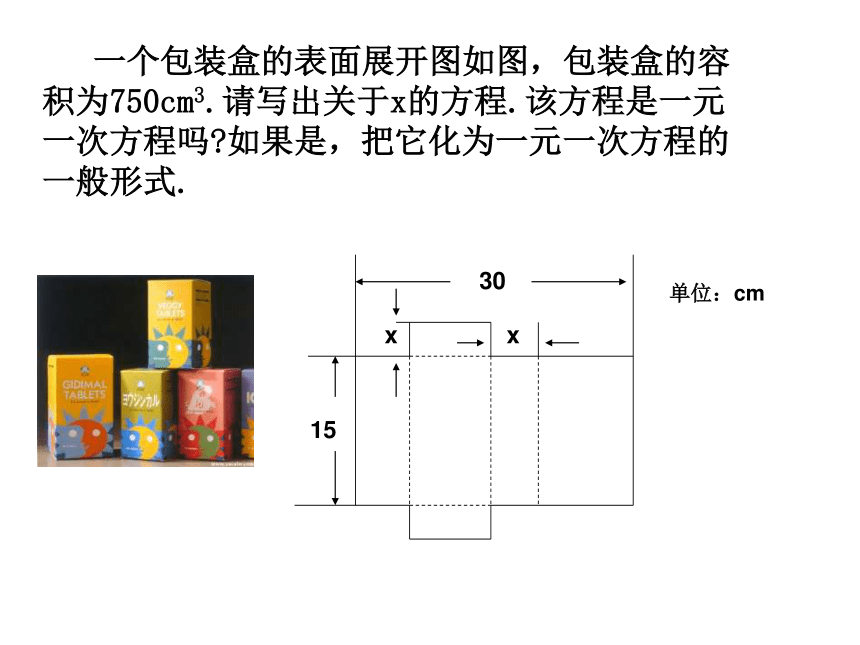
课件23张PPT。17.1 一元二次方程什么是方程?什么是方程的解(或根)?答:含有未知数的等式叫做方程。使方程两边成立的未知数的值叫做方程的解。曾学过哪些方程?分式方程,一元一次方程,二元一次方程。什么叫做一元一次方程?温故知新 一个包装盒的表面展开图如图,包装盒的容积为750cm3.请写出关于x的方程.该方程是一元一次方程吗?如果是,把它化为一元一次方程的一般形式.单位:cm解:设这块铁片的宽为x cm,那么它的长
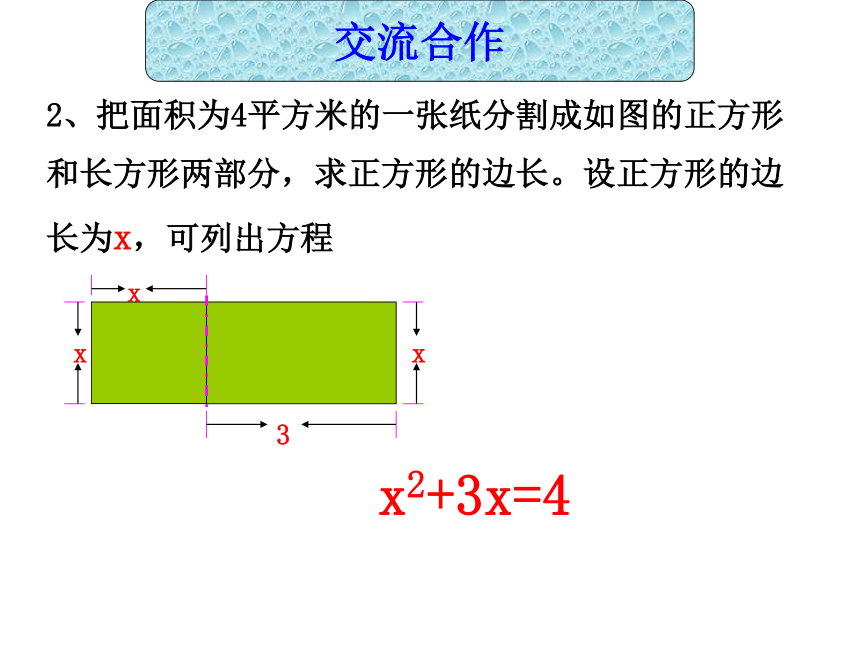
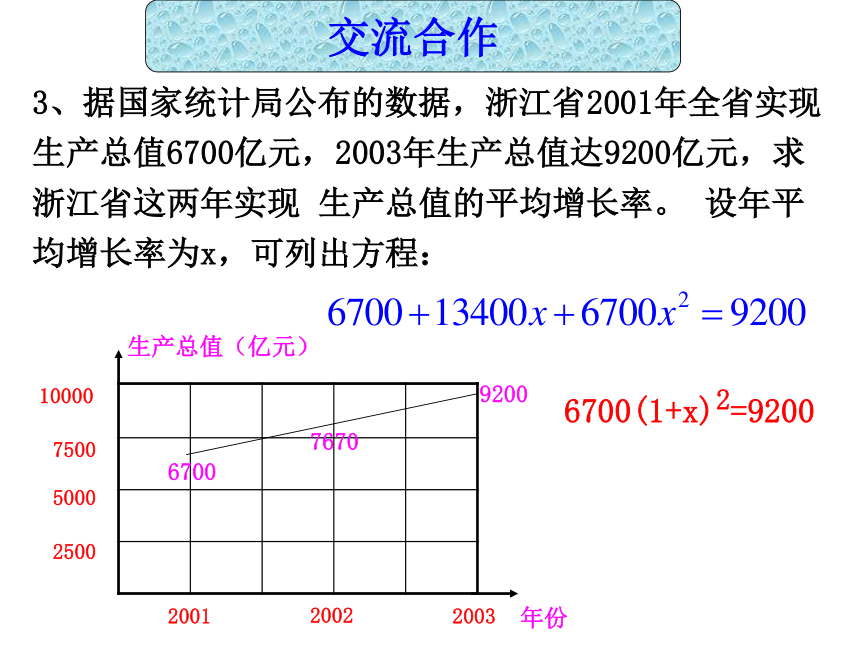
为(x+5) cm. 根据题意,得x(x+5)=150. 去括号,得 x2+5x=150.1、剪一块面积为150cm2的长方形铁片,使它的长比宽多5cm,这块铁片应怎样剪?根据题意列方程交流合作2、把面积为4平方米的一张纸分割成如图的正方形和长方形两部分,求正方形的边长。设正方形的边长为x,可列出方程 xx2+3x=4交流合作3、据国家统计局公布的数据,浙江省2001年全省实现生产总值6700亿元,2003年生产总值达9200亿元,求浙江省这两年实现 生产总值的平均增长率。 设年平均增长率为x,可列出方程:25005000750010000200120022003年份生产总值(亿元)9200767067006700(1+x)2=9200交流合作问:有什么相同的特点?共同点:(1)两边都是整式;
(2)只含有一个未知数;
(3)未知数最高次数为2次观察所列方程具有以上三个特点的方程称为一元二次方程(1) x2+5x=150.能使一元二次方程两边相等的未知数的值叫一元二次方程的解(或根)判断下列方程是否为一元二次方程:① 10x2=9 ( ) ②2(x-1)=3x ( )
③2x2-3x-1=0 ( ) ( )
⑤2xy-7=0 ( ) ⑥9x2=5-4x ( )
⑦4x2=5x ( ) ⑧3y2+4=5y ( ) √√√√×××√( )√判断下列方程是一元二次方程吗?√√√√√ 其中ax2 ,bx, c分别称为二次项,
一次项,常数项. ax2 + bx + c = 0注意:要确定一元二次方程的系数和常数项 ,必须先将方程化为一般形式二次项系数一次项系数常数项(a≠0) 在写一元二次方程的一般形式时,通常按未知数的次数从高到低排列,即先写二次项,再写一次项,最后是常数项。 把一元二次方程(x-√5 )(x+√5 )+(2x-1)2=0
化为一般形式,正确的是( )
A、5x2-4x-4=0B、x2-5=0C、5x2-2x+1=0D、5x2-4x+6=0A例1、把下列方程化成一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.注意:1.要先化成 ax2+bx+c=0 的一般形式。
2.若方程中含有整式乘法,要先利用法则展开再进行等式变形。
3.在写一元二次方程一般式时,通常按未知数次数从高到低排列,即先写二次项,再写一次项,最后是常数项。写系数时,要带上前面的符号。 1、把下列方程化为一元二次方程的形式,并写出它的二次项系数、一次项系数和常数项:练一练3x2-5x+1=0x2+x-8=0-7x2+4=03-51-8411-70例2、已知一元二次方程 2x2+bx+c=0的两个根分别为x1=2.5和x2=-3,求这个方程.解:将x1=2.5和x2=-3带入方程 2x2+bx+c=0得
2×(2.5)2+2.5b+c=0
2×(-3)2+(-3)b+c=0解得 b=1
c=-15所以这个一元二次方程是2x2+x-15=0变型、已知,关于x的方程 (2m-1)x2-(m-1)x=5m
是一元二次方程, 求m的取值范围.解:∵原方程是一元二次方程 ∴ 2m-1≠0 能使一元二次方程两边相等的未知数的值叫一元二次方程的解(或根).做一做 判断未知数的值x= -1,x=0,x=2是不是方程x2-2=x的根.1、判断下列各题括号内未知数的值是不是方程的根:(1)x2-3x+2=0 (x1=1 x2=2 x3=3)练一练2、构造一个一元二次方程,要求:
(1)常数项为零;(2)有一根为2。3、已知关于x的一元二次方程x2+ax+a=0的一个根是3,求a的值。解:由题意得
把x=3代入方程x2+ax+a=0得,32+3a+a=09+4a=04a=-9练一练课堂小结1.了解一元二次方程的概念和一般形式.
2.会判别一元二次方程的二次项系数,一次项系数和常数项.
3.注意:一元二次方程的二次项系数不能为零.课本P21页:
1.课内练习
2. 课后习题17.1 已知关于x的一元二次方程 ax2+bx+c=0 (a≠0)一个根为1, 求a+b+c的值. 解:由题意得思考:若 a+b+c=0,你能通过观察,求出方程ax2+bx+c=0 (a≠0)一个根吗? 解:由题意得∴方程ax2+bx+c=0 (a≠0)一个根是1.拓展:若 a-b +c=0, 你能通过观察,求出方程ax2+bx+c=0 (a≠0)一个根吗? 4a+2b +c=0拓展练习
为(x+5) cm. 根据题意,得x(x+5)=150. 去括号,得 x2+5x=150.1、剪一块面积为150cm2的长方形铁片,使它的长比宽多5cm,这块铁片应怎样剪?根据题意列方程交流合作2、把面积为4平方米的一张纸分割成如图的正方形和长方形两部分,求正方形的边长。设正方形的边长为x,可列出方程 xx2+3x=4交流合作3、据国家统计局公布的数据,浙江省2001年全省实现生产总值6700亿元,2003年生产总值达9200亿元,求浙江省这两年实现 生产总值的平均增长率。 设年平均增长率为x,可列出方程:25005000750010000200120022003年份生产总值(亿元)9200767067006700(1+x)2=9200交流合作问:有什么相同的特点?共同点:(1)两边都是整式;
(2)只含有一个未知数;
(3)未知数最高次数为2次观察所列方程具有以上三个特点的方程称为一元二次方程(1) x2+5x=150.能使一元二次方程两边相等的未知数的值叫一元二次方程的解(或根)判断下列方程是否为一元二次方程:① 10x2=9 ( ) ②2(x-1)=3x ( )
③2x2-3x-1=0 ( ) ( )
⑤2xy-7=0 ( ) ⑥9x2=5-4x ( )
⑦4x2=5x ( ) ⑧3y2+4=5y ( ) √√√√×××√( )√判断下列方程是一元二次方程吗?√√√√√ 其中ax2 ,bx, c分别称为二次项,
一次项,常数项. ax2 + bx + c = 0注意:要确定一元二次方程的系数和常数项 ,必须先将方程化为一般形式二次项系数一次项系数常数项(a≠0) 在写一元二次方程的一般形式时,通常按未知数的次数从高到低排列,即先写二次项,再写一次项,最后是常数项。 把一元二次方程(x-√5 )(x+√5 )+(2x-1)2=0
化为一般形式,正确的是( )
A、5x2-4x-4=0B、x2-5=0C、5x2-2x+1=0D、5x2-4x+6=0A例1、把下列方程化成一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.注意:1.要先化成 ax2+bx+c=0 的一般形式。
2.若方程中含有整式乘法,要先利用法则展开再进行等式变形。
3.在写一元二次方程一般式时,通常按未知数次数从高到低排列,即先写二次项,再写一次项,最后是常数项。写系数时,要带上前面的符号。 1、把下列方程化为一元二次方程的形式,并写出它的二次项系数、一次项系数和常数项:练一练3x2-5x+1=0x2+x-8=0-7x2+4=03-51-8411-70例2、已知一元二次方程 2x2+bx+c=0的两个根分别为x1=2.5和x2=-3,求这个方程.解:将x1=2.5和x2=-3带入方程 2x2+bx+c=0得
2×(2.5)2+2.5b+c=0
2×(-3)2+(-3)b+c=0解得 b=1
c=-15所以这个一元二次方程是2x2+x-15=0变型、已知,关于x的方程 (2m-1)x2-(m-1)x=5m
是一元二次方程, 求m的取值范围.解:∵原方程是一元二次方程 ∴ 2m-1≠0 能使一元二次方程两边相等的未知数的值叫一元二次方程的解(或根).做一做 判断未知数的值x= -1,x=0,x=2是不是方程x2-2=x的根.1、判断下列各题括号内未知数的值是不是方程的根:(1)x2-3x+2=0 (x1=1 x2=2 x3=3)练一练2、构造一个一元二次方程,要求:
(1)常数项为零;(2)有一根为2。3、已知关于x的一元二次方程x2+ax+a=0的一个根是3,求a的值。解:由题意得
把x=3代入方程x2+ax+a=0得,32+3a+a=09+4a=04a=-9练一练课堂小结1.了解一元二次方程的概念和一般形式.
2.会判别一元二次方程的二次项系数,一次项系数和常数项.
3.注意:一元二次方程的二次项系数不能为零.课本P21页:
1.课内练习
2. 课后习题17.1 已知关于x的一元二次方程 ax2+bx+c=0 (a≠0)一个根为1, 求a+b+c的值. 解:由题意得思考:若 a+b+c=0,你能通过观察,求出方程ax2+bx+c=0 (a≠0)一个根吗? 解:由题意得∴方程ax2+bx+c=0 (a≠0)一个根是1.拓展:若 a-b +c=0, 你能通过观察,求出方程ax2+bx+c=0 (a≠0)一个根吗? 4a+2b +c=0拓展练习
