人教版数学九年级下册 28.2.2应用举例学案(含答案)
文档属性
| 名称 | 人教版数学九年级下册 28.2.2应用举例学案(含答案) | 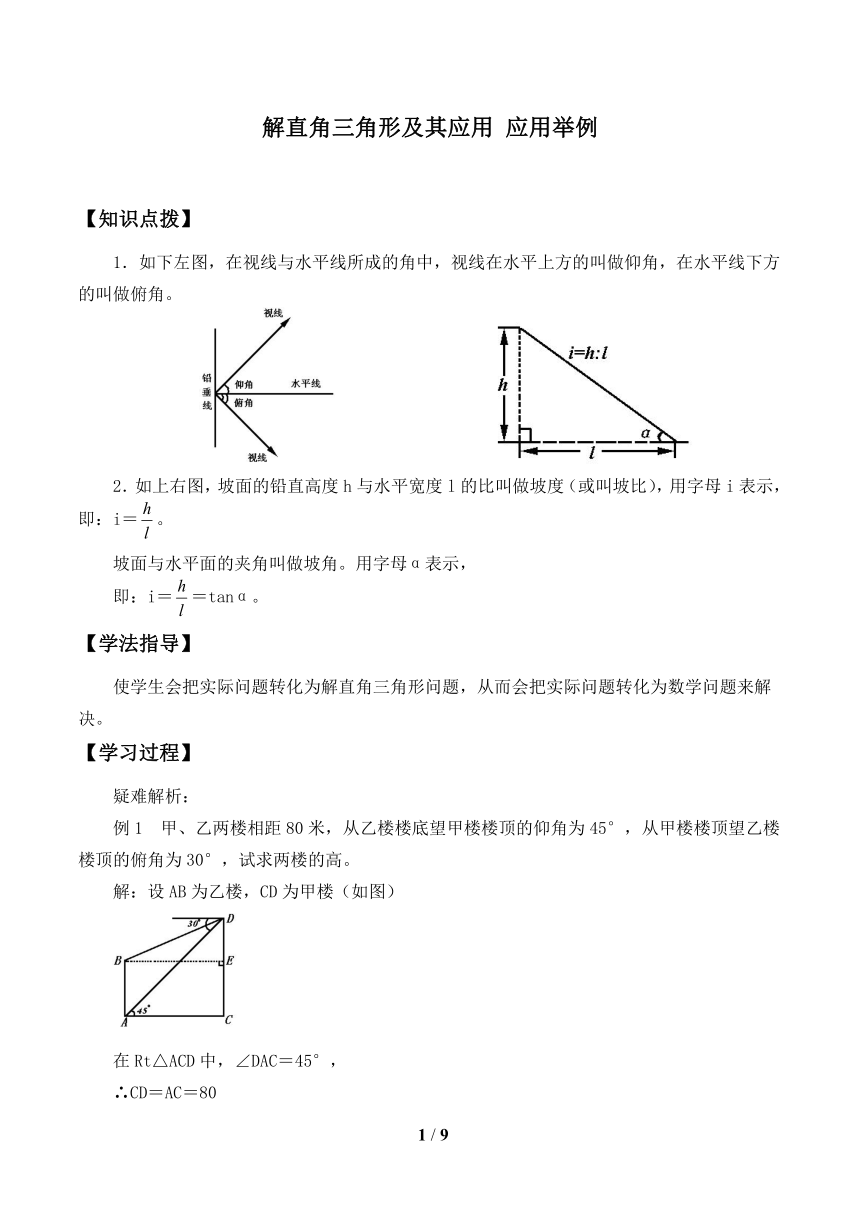 | |
| 格式 | doc | ||
| 文件大小 | 127.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-11 11:18:56 | ||
图片预览




文档简介
解直角三角形及其应用 应用举例
【知识点拨】
1.如下左图,在视线与水平线所成的角中,视线在水平上方的叫做仰角,在水平线下方的叫做俯角。
2.如上右图,坡面的铅直高度h与水平宽度l的比叫做坡度(或叫坡比),用字母i表示,即:i=。
坡面与水平面的夹角叫做坡角。用字母α表示,
即:i==tanα。
【学法指导】
使学生会把实际问题转化为解直角三角形问题,从而会把实际问题转化为数学问题来解决。
【学习过程】
疑难解析:
例1 甲、乙两楼相距80米,从乙楼楼底望甲楼楼顶的仰角为45°,从甲楼楼顶望乙楼楼顶的俯角为30°,试求两楼的高。
解:设AB为乙楼,CD为甲楼(如图)
在Rt△ACD中,∠DAC=45°,
∴CD=AC=80
过B作BE⊥CD于点E,设AB=x
则DE=(80-x)米
在Rt△BED中,∠DBE=30°,BE=AC=80米
tan∠DBE= 即=
解得:x=80(1-)
则AB=80(1-)(米)
CD=80米
答:甲楼高为80米,乙楼高为80(1-)米。
说明:本例构造了两个直角三角形,通过解直角三角形来求解。
例2 如图,一水坝横断面为等腰梯形ABCD,斜坡AB的坡度为1∶,坡面AB的水平宽度为3米,上底宽AD为4米,求坡角B,坝高AE和坝底宽BC各是多少?
分析:将实际问题转化为数学问题,如图所示,实际已知i=1∶,即知=,BE=3 AD=4,求∠B、AE、BC.此题实质转化为解直角三角形的问题。
解:∵tanB=i==
又∵∠B是锐角 ∴∠B=30°
又∵=i=
又∵BE=3
∴AE=3×=3
BC=2BE+AD=2×3+4
=4+6
答:坡角B为30°,坝高AE为3米,坝底宽为(6+4)米。
注意:(1)解应用题时,解题过程中可以不写各数量的单位,但最后作答时务必写清单位名称。
(2)应用问题尽管题型千变万化,但关键是设法化归为解直角三角形同题,必要时应添加辅助线,构造出直角三角形。梯形也是通过作底面高线来构造直角三角形。
(3)本题主要应用坡度是坡角的正切函数而求出坡角,运用坡度的概念求出梯形高,运用等腰梯形性质求出底边。
例3 如图一轮船自西向东航行,在A处测得某岛C,在北偏东60°的方向上,船前进8海里后到达B,再测C岛,在北偏东30°的方向上,问船再前进多少海里与C岛最近?最近距离是多少?
分析:将实际问题转化为数学问题,并构造出与实际问题有关的直角三角形,如图所示,船沿AB方向继续前进至D处与C岛最近,此问题实质就是已知∠A=90°-60°=30°,∠ABC=90°+30°=120°,AB=8海里,求BD和CD的解直角三角形问题。
解:根据题设可知△ABC中,∠CAB=30° ∠ABC=120°,AB=BC=8
∴最近距离即为C到AB所在直线的垂线段CD的长度。
在Rt△CBD中,BC=8,∠BCD=60°
于是,BD=BC·cos60°=8×=4(海里)
CD=BC·sin60°=8×=4 (海里)
答:船再前进4海里就与C最近,最近距离是4海里。
注意:根据题意准确画出示意图是解这类题的前提和保障。
典例精评
例1 如图,在山顶B处有一铁塔AB,在A处测得地面上一点C的俯角为60°,在塔底B测得C俯角为45°,已知AB=30米,求山高DB的值。
分析 本题图形中有两个直角三角形,它们有公共边DC,所以用含有BD的代数式表示DC和AD,而DC和AD在Rt△ADC中,可利用三角函数关系式列出DC的方程,由BD=DC,得到结论。
解:由已知条件得:
BD=DC,AD=30+BD,∠ACD=60°
在Rt△ADC中,tan60°===
∴DC=15(+1)(米)
∴BD=15(+1)(米)
答:山高DB为15(+1)米
例2 一段河坝的横断面为等腰梯形ABCD,试根据图中数据求出坡角α和坝底宽AD(如图所示)。
分析 此题应正确理解,应用坡度、坡角的概念及联系,即i=tanα=,将梯形问题,添加高线把梯形转化为两个直角三角形及矩形来解。
解:过C作CF⊥AD于F
∵AB=CD,BC∥AD
∴CF=BE=6,EF=BC=4
又∵i=1∶
∴AE=FD=·CF=×6=6(米)
∴AD=AE+EF+FD=4+12(米)
∵tanα==i==
∴α=30°
答:坡角α=30°,坝底宽AD=(4+12)米。
考点预测
利用三角函数知识解决实际问题在每年的中考题中都有可能出现,并且多以综合题形式出现。
例1 如图,在平地D处测得树顶A的仰角为30°,向树前进10米,到达C处,再测得树顶A的仰角为45°,求树高AB.(结果保留根号)
分析:先将实际问题转化为数学问题,构造出直角三角形
已知∠ABC=90°,∠ACB=45°,∠ADB=30°,CD=10米,求AB.
由于AB所在的Rt△ABC和Rt△ABD都不够解三角形的条件,所以需设AB=x,同时解两个直角三角形,得到关于x的方程再求出x的值。
解:设AB=x米,则在Rt△ABC和Rt△ABD中
BC=ABcot45° BD=AB·cot30°
∴CD=BD-BC=x(-1)
又∵CD=10 ∴x(-1)=10
∴x==5(+1)=5+5(米)
答:树高为5+5米。
此题为1998年辽宁省的中考试题,这实际上是利用三角板组合的图形题,类似这种类型题每年中考题选上都有几道,望多加注意。
例2 如图,在一座山的山顶B处用高为1米的测倾器望地面C、D两点,测得的俯角分别为60°和45°,若已知DC的长是20米,求山高BE。(结果可用根式表示)
解 在Rt△ACE中,有CE=AE·tan30°,
在Rt△ADE中,有DE=AE·tan45°,
∴DC=DE-CE=AE(tan45°-tan30°)
∴AE==(30+10)米
∴BE=AE-AB=(29+10)米
答:山高为(29+10)米。
例3 如图,上午8时,一条船从A处出发以15海里/时的速度向正北航行,9时45分到达B处,从A处测得灯塔C在北偏西26°,从B处测得灯塔C在北偏西52°,求B处到灯塔C的距离。
解 ∵∠CBN=∠C+∠BAC
∴∠C=52°-26°=26°
∴∠C=∠BAC,∴AB=BC
又∵AB=15×(1+)=26.25海里
∴B处到灯塔C的距离CB为26.25海里。
例4 如图,从20米高的甲楼顶A处望乙楼顶C处的仰角是30°,望乙楼底D处的俯角是45°,求乙楼的高度。(精确到0.1米,≈1.414,≈1.732)
解 过A点作AE⊥CD,垂足是E,
∵AB∥CD,AE∥BD
∴DE=AB=20米
在Rt∠ADE中,∠DAE=45°,DE=20米,
∴AE=20米
在Rt△ACE中,∠CAE=30°,AE=20米
∴CE=AE·tan30°=米
∴CD=CE+ED= +20=20(+1)
≈31.5米
答:乙楼的高约是31.5米。
同步达纲练习
知识强化:
一、填空题
1.在△ABC中,∠A=45°,∠B=30°,AB=2,则BC= ,AC= 。
2.在△ABC中,已知AB=4,AC=6,∠A=60°,则BC= 。
3.在△ABC中,∠A=120°,b=5,c=8,则S△ABC= 。
4.已知△ABC中,AB=2,AC=8,BC=6,BD是中线,则BD= 。
5.已知斜坡AB长为60米,AB的坡度i=1∶,则斜坡AB的高度为 米。
6.如图,从楼A处望地面C、D两点的俯角分别为45°和30°,若CD距离为100米,则楼AB高为 。
7.等腰直角三角形一腰上的中线与底边夹角的余弦值为 。
8.在△ABC中,∠A=120°,AB=10,AC=5,则sinB·sinC= 。
二、选择题
1.Rt△ABC中,∠C=90°,a=2,b=2,那么下面结论中不正确的是( )
A.c=4 B、CotA= C.sinA+cosB=1 D.∠B=30°
2.在△ABC中,∠A=30°,∠B=45°,AC=8,则BC的长为( )
A.4 B.4 C.4 D.4
3.如图,从山顶A望地面C、D两点,它们的俯角分别为45°、30°,如果测得CD为100米,那么山高AB等于( )
A.100米 B. ×100米 C.50 D.50(+1)米
4.某个水库大坝的横断面是梯形,坝内斜坡的坡度i=1∶,坝外斜坡的坡度i=1∶1,那么两个坡角的和为( )
A.90° B.75° C.60° D.105°
素质优化:
1. 一船以每小时20千米的速度向正东航行,起初船在A处看见一灯塔B在船的北偏东60°,2小时后,船在C处看见这个灯塔在船的北偏东45°,求灯塔B到船的航线AC的距离。
2.如图,水库大坝的横断面是梯形,坝顶宽8m,坝高25m,斜坡AB的坡度i=1∶2.8,斜坡CD的坡度i′=1∶2.4,求斜坡AB的坡角α,坝底宽AD和斜坡AB的长(精确到0.1m)。
创新深化:
如图,敌人在某岛周围20海里的区域内布设了水雷,某舰由西向东航行,起初在O点处观察此岛的北偏东60°处,航行30海里到达B时,再观察此岛,在北偏东30°处,如果不改变航向,继续向东航行,此舰有没有触雷的危险。
参考答案
知识强化:
一、1.2-2,- 2.2
3.30 4.
5.30 6.50(+1)
7. 8.
二、1.D 2.B 3.D 4.B
素质优化:
1.(80 +120)千米
2.AD=138米,AB=74.3米
创新深化:
∵AC=15>0 ∴没有触雷的危险
PAGE
9 / 9
【知识点拨】
1.如下左图,在视线与水平线所成的角中,视线在水平上方的叫做仰角,在水平线下方的叫做俯角。
2.如上右图,坡面的铅直高度h与水平宽度l的比叫做坡度(或叫坡比),用字母i表示,即:i=。
坡面与水平面的夹角叫做坡角。用字母α表示,
即:i==tanα。
【学法指导】
使学生会把实际问题转化为解直角三角形问题,从而会把实际问题转化为数学问题来解决。
【学习过程】
疑难解析:
例1 甲、乙两楼相距80米,从乙楼楼底望甲楼楼顶的仰角为45°,从甲楼楼顶望乙楼楼顶的俯角为30°,试求两楼的高。
解:设AB为乙楼,CD为甲楼(如图)
在Rt△ACD中,∠DAC=45°,
∴CD=AC=80
过B作BE⊥CD于点E,设AB=x
则DE=(80-x)米
在Rt△BED中,∠DBE=30°,BE=AC=80米
tan∠DBE= 即=
解得:x=80(1-)
则AB=80(1-)(米)
CD=80米
答:甲楼高为80米,乙楼高为80(1-)米。
说明:本例构造了两个直角三角形,通过解直角三角形来求解。
例2 如图,一水坝横断面为等腰梯形ABCD,斜坡AB的坡度为1∶,坡面AB的水平宽度为3米,上底宽AD为4米,求坡角B,坝高AE和坝底宽BC各是多少?
分析:将实际问题转化为数学问题,如图所示,实际已知i=1∶,即知=,BE=3 AD=4,求∠B、AE、BC.此题实质转化为解直角三角形的问题。
解:∵tanB=i==
又∵∠B是锐角 ∴∠B=30°
又∵=i=
又∵BE=3
∴AE=3×=3
BC=2BE+AD=2×3+4
=4+6
答:坡角B为30°,坝高AE为3米,坝底宽为(6+4)米。
注意:(1)解应用题时,解题过程中可以不写各数量的单位,但最后作答时务必写清单位名称。
(2)应用问题尽管题型千变万化,但关键是设法化归为解直角三角形同题,必要时应添加辅助线,构造出直角三角形。梯形也是通过作底面高线来构造直角三角形。
(3)本题主要应用坡度是坡角的正切函数而求出坡角,运用坡度的概念求出梯形高,运用等腰梯形性质求出底边。
例3 如图一轮船自西向东航行,在A处测得某岛C,在北偏东60°的方向上,船前进8海里后到达B,再测C岛,在北偏东30°的方向上,问船再前进多少海里与C岛最近?最近距离是多少?
分析:将实际问题转化为数学问题,并构造出与实际问题有关的直角三角形,如图所示,船沿AB方向继续前进至D处与C岛最近,此问题实质就是已知∠A=90°-60°=30°,∠ABC=90°+30°=120°,AB=8海里,求BD和CD的解直角三角形问题。
解:根据题设可知△ABC中,∠CAB=30° ∠ABC=120°,AB=BC=8
∴最近距离即为C到AB所在直线的垂线段CD的长度。
在Rt△CBD中,BC=8,∠BCD=60°
于是,BD=BC·cos60°=8×=4(海里)
CD=BC·sin60°=8×=4 (海里)
答:船再前进4海里就与C最近,最近距离是4海里。
注意:根据题意准确画出示意图是解这类题的前提和保障。
典例精评
例1 如图,在山顶B处有一铁塔AB,在A处测得地面上一点C的俯角为60°,在塔底B测得C俯角为45°,已知AB=30米,求山高DB的值。
分析 本题图形中有两个直角三角形,它们有公共边DC,所以用含有BD的代数式表示DC和AD,而DC和AD在Rt△ADC中,可利用三角函数关系式列出DC的方程,由BD=DC,得到结论。
解:由已知条件得:
BD=DC,AD=30+BD,∠ACD=60°
在Rt△ADC中,tan60°===
∴DC=15(+1)(米)
∴BD=15(+1)(米)
答:山高DB为15(+1)米
例2 一段河坝的横断面为等腰梯形ABCD,试根据图中数据求出坡角α和坝底宽AD(如图所示)。
分析 此题应正确理解,应用坡度、坡角的概念及联系,即i=tanα=,将梯形问题,添加高线把梯形转化为两个直角三角形及矩形来解。
解:过C作CF⊥AD于F
∵AB=CD,BC∥AD
∴CF=BE=6,EF=BC=4
又∵i=1∶
∴AE=FD=·CF=×6=6(米)
∴AD=AE+EF+FD=4+12(米)
∵tanα==i==
∴α=30°
答:坡角α=30°,坝底宽AD=(4+12)米。
考点预测
利用三角函数知识解决实际问题在每年的中考题中都有可能出现,并且多以综合题形式出现。
例1 如图,在平地D处测得树顶A的仰角为30°,向树前进10米,到达C处,再测得树顶A的仰角为45°,求树高AB.(结果保留根号)
分析:先将实际问题转化为数学问题,构造出直角三角形
已知∠ABC=90°,∠ACB=45°,∠ADB=30°,CD=10米,求AB.
由于AB所在的Rt△ABC和Rt△ABD都不够解三角形的条件,所以需设AB=x,同时解两个直角三角形,得到关于x的方程再求出x的值。
解:设AB=x米,则在Rt△ABC和Rt△ABD中
BC=ABcot45° BD=AB·cot30°
∴CD=BD-BC=x(-1)
又∵CD=10 ∴x(-1)=10
∴x==5(+1)=5+5(米)
答:树高为5+5米。
此题为1998年辽宁省的中考试题,这实际上是利用三角板组合的图形题,类似这种类型题每年中考题选上都有几道,望多加注意。
例2 如图,在一座山的山顶B处用高为1米的测倾器望地面C、D两点,测得的俯角分别为60°和45°,若已知DC的长是20米,求山高BE。(结果可用根式表示)
解 在Rt△ACE中,有CE=AE·tan30°,
在Rt△ADE中,有DE=AE·tan45°,
∴DC=DE-CE=AE(tan45°-tan30°)
∴AE==(30+10)米
∴BE=AE-AB=(29+10)米
答:山高为(29+10)米。
例3 如图,上午8时,一条船从A处出发以15海里/时的速度向正北航行,9时45分到达B处,从A处测得灯塔C在北偏西26°,从B处测得灯塔C在北偏西52°,求B处到灯塔C的距离。
解 ∵∠CBN=∠C+∠BAC
∴∠C=52°-26°=26°
∴∠C=∠BAC,∴AB=BC
又∵AB=15×(1+)=26.25海里
∴B处到灯塔C的距离CB为26.25海里。
例4 如图,从20米高的甲楼顶A处望乙楼顶C处的仰角是30°,望乙楼底D处的俯角是45°,求乙楼的高度。(精确到0.1米,≈1.414,≈1.732)
解 过A点作AE⊥CD,垂足是E,
∵AB∥CD,AE∥BD
∴DE=AB=20米
在Rt∠ADE中,∠DAE=45°,DE=20米,
∴AE=20米
在Rt△ACE中,∠CAE=30°,AE=20米
∴CE=AE·tan30°=米
∴CD=CE+ED= +20=20(+1)
≈31.5米
答:乙楼的高约是31.5米。
同步达纲练习
知识强化:
一、填空题
1.在△ABC中,∠A=45°,∠B=30°,AB=2,则BC= ,AC= 。
2.在△ABC中,已知AB=4,AC=6,∠A=60°,则BC= 。
3.在△ABC中,∠A=120°,b=5,c=8,则S△ABC= 。
4.已知△ABC中,AB=2,AC=8,BC=6,BD是中线,则BD= 。
5.已知斜坡AB长为60米,AB的坡度i=1∶,则斜坡AB的高度为 米。
6.如图,从楼A处望地面C、D两点的俯角分别为45°和30°,若CD距离为100米,则楼AB高为 。
7.等腰直角三角形一腰上的中线与底边夹角的余弦值为 。
8.在△ABC中,∠A=120°,AB=10,AC=5,则sinB·sinC= 。
二、选择题
1.Rt△ABC中,∠C=90°,a=2,b=2,那么下面结论中不正确的是( )
A.c=4 B、CotA= C.sinA+cosB=1 D.∠B=30°
2.在△ABC中,∠A=30°,∠B=45°,AC=8,则BC的长为( )
A.4 B.4 C.4 D.4
3.如图,从山顶A望地面C、D两点,它们的俯角分别为45°、30°,如果测得CD为100米,那么山高AB等于( )
A.100米 B. ×100米 C.50 D.50(+1)米
4.某个水库大坝的横断面是梯形,坝内斜坡的坡度i=1∶,坝外斜坡的坡度i=1∶1,那么两个坡角的和为( )
A.90° B.75° C.60° D.105°
素质优化:
1. 一船以每小时20千米的速度向正东航行,起初船在A处看见一灯塔B在船的北偏东60°,2小时后,船在C处看见这个灯塔在船的北偏东45°,求灯塔B到船的航线AC的距离。
2.如图,水库大坝的横断面是梯形,坝顶宽8m,坝高25m,斜坡AB的坡度i=1∶2.8,斜坡CD的坡度i′=1∶2.4,求斜坡AB的坡角α,坝底宽AD和斜坡AB的长(精确到0.1m)。
创新深化:
如图,敌人在某岛周围20海里的区域内布设了水雷,某舰由西向东航行,起初在O点处观察此岛的北偏东60°处,航行30海里到达B时,再观察此岛,在北偏东30°处,如果不改变航向,继续向东航行,此舰有没有触雷的危险。
参考答案
知识强化:
一、1.2-2,- 2.2
3.30 4.
5.30 6.50(+1)
7. 8.
二、1.D 2.B 3.D 4.B
素质优化:
1.(80 +120)千米
2.AD=138米,AB=74.3米
创新深化:
∵AC=15>0 ∴没有触雷的危险
PAGE
9 / 9
