人教版数学九年级下册第二十八章 锐角三角函数小结与复习单元测试(含答案)
文档属性
| 名称 | 人教版数学九年级下册第二十八章 锐角三角函数小结与复习单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 338.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-11 13:37:39 | ||
图片预览




文档简介
人教九年级下 单元测试
第28章
班级________ 姓名________
一、选择题(本大题共10小题,每小题4分,满分40分)
1.在Rt△ABC中,∠C=90°,AB=3BC,则sin B的值为( )
A. B. C. D.
2.若α为锐角,且cos α=,则( )
A.0°<α <30° B.30°<α <45° C.45°<α <60° D.60°<α <90°
3.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
A.sin B= B.sin B= C.sin B= D.sin B=
4.在Rt△ABC中,∠C=90°,tan A=,则cos B的值为( )
A. B. C. D.
5.如图,△ABC与△A'B'C'都是等腰三角形,且AB=AC=5,A'B'=A'C'=3.若∠B+∠B'=90°,则△ABC与△A'B'C'的面积比为( )
A.25∶9 B.5∶3 C.∶ D.5∶3
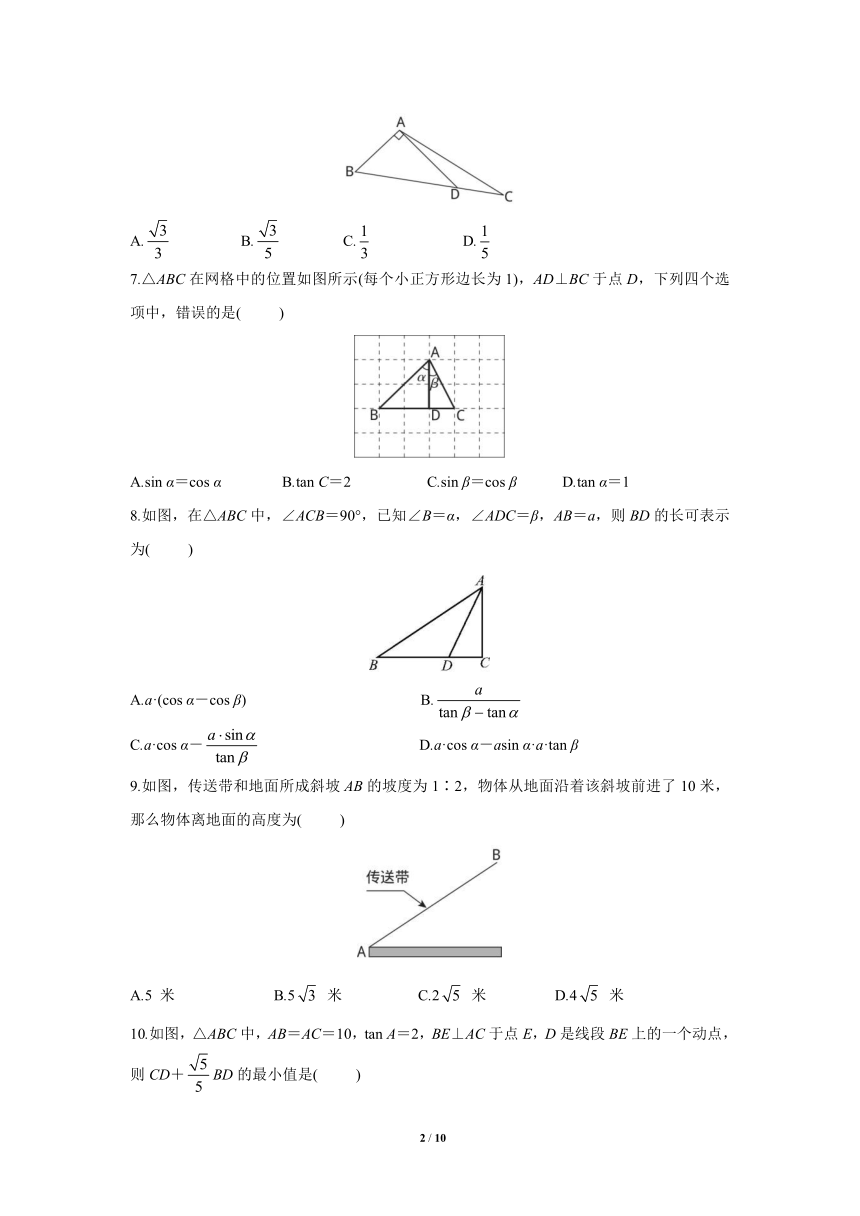
6.如图,在Rt△ABD中,延长斜边BD到点C,使DC=BD,连接AC.若tan B=,则tan ∠CAD的值为( )
A. B. C. D.
7.△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于点D,下列四个选项中,错误的是( )
A.sin α=cos α B.tan C=2 C.sin β=cos β D.tan α=1
8.如图,在△ABC中,∠ACB=90°,已知∠B=α,∠ADC=β,AB=a,则BD的长可表示为( )
A.a·(cos α-cos β) B.
C.a·cos α- D.a·cos α-asin α·a·tan β
9.如图,传送带和地面所成斜坡AB的坡度为1∶2,物体从地面沿着该斜坡前进了10米,那么物体离地面的高度为( )
A.5 米 B.5 米 C.2 米 D.4 米
10.如图,△ABC中,AB=AC=10,tan A=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是( )
A.2 B.4 C.5 D.10
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,某山坡的坡度为i=1∶,小辰从山脚A出发,沿山坡向上走了200米到达点B,则小辰上升了 米.
12.如图,四边形ABCD的对角线AC,BD相交于点O,且BD平分AC.若BD=8,AC=6,∠BOC=120°,则四边形ABCD的面积为 .(结果保留根号)
13.如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行 小时即可到达.(结果保留根号)
14.一般地,当α,β为任意角时,sin(α+β)与sin(α-β)的值可以用下面的公式求得:sin(α+β)=sin α·cos β+cos α·sin β;sin(α-β)=sin α·cos β-cos α·sin β.例如sin 90°=sin(60°+30°)=sin 60°·cos 30°+cos 60°·sin 30°=×+×=1.则类似地,可以求得
(1)sin 15°的值是 ;
(2)sin 75°的值是 .
三、(本大题共2小题,每小题8分,满分16分)
15.计算:-cos 30°+sin 45°.
16.如图,已知AB是☉O的直径,CD是弦,且CD⊥AB,BC=6,AC=8,求sin ∠ABD的值.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在△ABC中,∠A=30°,cos B=,AC=6.求AB的长.
18.如图,山顶有一座塔AB,塔高33 m.计划在塔的正下方沿直线CD开通穿山隧道EF.从与E点相距80 m的C处测得A,B的仰角分别为27°,22°,从与F点相距50 m的D处测得A的仰角为45°,求隧道EF的长度.(参考数据:tan 22°≈0.40,tan 27°≈0.51)
五、(本大题共2小题,每小题10分,满分20分)
19.如图,某数学活动小组为测量学校旗杆AB的高度,从旗杆正前方2米处的点C出发,沿斜面坡度i=1∶的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A,B,C,D,E在同一平面内,AB⊥BC,AB∥DE.求旗杆AB的高度.(结果保留根号,参考数据:sin 37°≈,cos 37°≈,tan 37°≈)
20.如图,某海监船以60海里/小时的速度从A处出发沿正西方向巡逻,一艘可疑船只在A的西北方向的C处,海监船航行1.5小时到达B处时接到报警,需巡査此可疑船只,此时可疑船只仍在B的北偏西30°方向的C处,然后,可疑船只以一定速度向正西方向逃离,海监船立刻加速以90海里/小时的速度追击,在D处海监船追到可疑船只,D在B的北偏西60°方向.(结果保留根号)
(1)求B,C两处之间的距离;
(2)求海监船追到可疑船只所用的时间.
六、(本题满分12分)
21.如图,已知△ABC中,∠ACB=90°,D是边AB的中点,P是边AC上一动点,BP与CD相交于点E.
(1)如果BC=6,AC=8,且P为AC的中点,求线段BE的长;
(2)连接PD,如果PD⊥AB,且CE=2,ED=3,求cos A的值.
七、(本题满分12分)
22.对于钝角α,定义它的三角函数值如下:
sin α=sin(180°-α),cos α=-cos(180°-α).
(1)求sin 120°,cos 120°,sin 150°的值;
(2)若一个三角形的三个内角的比是1∶1∶4,A,B是这个三角形的两个顶点,sin A,cos B是方程4x2-mx-1=0的两个不相等的实数根,求m的值及∠A,∠B的大小.
八、(本题满分14分)
23.将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2,P是AC上的一个动点.
(1)当点P运动到∠ABC的平分线上时,连接DP,求DP的长;
(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;
(3)当点P运动到什么位置时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上 求出此时 DPBQ的面积.
参 考 答 案
1.D 2.D 3.C 4.A 5.A 6.D 7.C 8.C 9.C 10.B
11.100 12.12 13. 14.(1) (2)
15.解:原式=-×+×=-+1=0.
16.解:由条件可知∠ABD=∠ABC,∵AB为☉O的直径,∴∠ACB=90°,又∵BC=6,AC=8,∴AB=10,∴sin ∠ABD=sin ∠ABC==.
17.解:过点C作CD⊥AB于点D.∵∠A=30°,∴CD=AC=3,AD=AC·cos A=9.在Rt△BCD中,设BD=4x,∴BC=5x.由勾股定理得CD=3x.由题意得3x=3,解得x=,∴BD=4,∴AB=AD+BD=9+4.
18.解:延长AB交CD于点H,∴AH⊥CD.在Rt△AHD中,∠D=45°,∴AH=DH.在Rt△AHC中,AH=CH·tan ∠ACH≈0.51CH.在Rt△BHC中,BH=CH·tan ∠BCH≈0.4CH,由题意得0.51CH-0.4CH=33,解得CH=300,∴EH=CH-CE=220,BH=120,∴AH=AB+BH=153,∴DH=AH=153,∴HF=DH-DF=103,∴EF=EH+FH=323.答:隧道EF的长度约为323 m.
19.解:延长ED交BC的延长线于点F,∴∠CFD=90°.∵tan ∠DCF=i==,∴∠DCF=30°.∵CD=4,∴DF=2,CF=CD·cos ∠DCF=2,∴BF=BC+CF=2+2=4.过点E作EG⊥AB于点G,∴GE=BF=4,GB=EF=ED+DF=3.5.又∵∠AEG=37°,∴AG=GE·tan ∠AEG=4·tan 37°,∴AB=AG+BG=4·tan 37°+3.5≈3+3.5,答:旗杆AB的高度约为(3+3.5)米.
20.解:(1)过点C作CE⊥AB于点E,则∠CEA=90°,∠CBE=60°.由题意得AB=60×1.5=90,∠CAB=45°,∴△ACE是等腰直角三角形.∴CE=AE,CE=BE,BC=2BE.设BE=x,则CE=x,AE=BE+AB=x+90,∴x=x+90,解得x=45+45,∴BC=2x=90+90.答:B,C两处之间的距离为(90+90)海里.
(2)过点D作DF⊥AB,交AB的延长线于点F,∴DF=CE=x=135+45,∠DBF=90°-60°=30°,∴BD=2DF=270+90,∴海监船追到可疑船只所用的时间为=(3+)小时.答:海监船追到可疑船只所用的时间为(3+)小时.
21.解:(1)∵P为AC的中点,AC=8,∴CP=4.∵∠ACB=90°,BC=6,∴BP=2.∵D是边AB的中点,P为AC的中点,∴点E是△ABC的重心,∴BE=BP=.
(2)如图,过点B作BF∥CA,交CD的延长线于点F,∴==.∵BD=DA,∴FD=DC,BF=AC.∵CE=2,ED=3,∴CD=5,∴EF=8,∴===,∴=,∴=.设CP=k,∴PA=3k.∵PD⊥AB,D是边AB的中点,∴PA=PB=3k,∴BC=2k,∴AB=2k.∵AC=4k,∴cos A=.
22.解:(1)由题意得sin 120°=sin(180°-120°)=sin 60°=,cos 120°=-cos(180°-120°)=-cos 60°=-,sin 150°=sin(180°-150°)=sin 30°=.
(2)∵三角形的三个内角的比是1∶1∶4,∴三个内角分别为30°,30°,120°.①当∠A=30°,∠B=120°时,方程的两根为,-,将x=代入方程,得4×()2-m×-1=0,解得m=0,经检验,-是方程4x2-1=0的根,∴m=0符合题意;②当∠A=120°,∠B=30°时,方程的两根为,,不符合题意;③当∠A=30°,∠B=30°时,方程的两根为,,将x=代入方程,得4×()2-m×-1=0,解得m=0,经检验,不是方程4x2-1=0的根,不符合题意.综上可知m=0,∠A=30°,∠B=120°.
23.解:在Rt△ABC中,AB=2,∠BAC=30°,∴BC=,AC=3.
(1)如图1,作DF⊥AC.∵Rt△ACD中,AD=CD,∴DF=AF=CF=.∵BP平分∠ABC,∴∠PBC=30°,∴CP=BC·tan 30°=1,∴PF=,∴DP==.
(2)当点P位置如图2所示时,根据(1)中结论,DF=,∠ADF=45°.又∵PD=BC=,∴cos ∠PDF==,∴∠PDF=30°,∴∠PDA=∠ADF-∠PDF=15°.当点P位置如图3所示时,同理得∠PDF=30°.∴∠PDA=∠ADF+∠PDF=75°.故∠PDA的度数为15°或75°.
(3)当点P运动到边AC的中点(如图4),即CP=时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上.∵四边形DPBQ为平行四边形,∴BC∥DP.∵∠ACB=90°,∴∠DPC=90°,即DP⊥AC.又∵在Rt△ABC中,AB=2,BC=,∴根据勾股定理得AC=3.∵△ACD为等腰直角三角形,∴DP=CP=AC=,∵BC∥DP,∴PC是平行四边形DPBQ的高,∴S DPBQ=DP·CP=.
1 / 10
第28章
班级________ 姓名________
一、选择题(本大题共10小题,每小题4分,满分40分)
1.在Rt△ABC中,∠C=90°,AB=3BC,则sin B的值为( )
A. B. C. D.
2.若α为锐角,且cos α=,则( )
A.0°<α <30° B.30°<α <45° C.45°<α <60° D.60°<α <90°
3.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
A.sin B= B.sin B= C.sin B= D.sin B=
4.在Rt△ABC中,∠C=90°,tan A=,则cos B的值为( )
A. B. C. D.
5.如图,△ABC与△A'B'C'都是等腰三角形,且AB=AC=5,A'B'=A'C'=3.若∠B+∠B'=90°,则△ABC与△A'B'C'的面积比为( )
A.25∶9 B.5∶3 C.∶ D.5∶3
6.如图,在Rt△ABD中,延长斜边BD到点C,使DC=BD,连接AC.若tan B=,则tan ∠CAD的值为( )
A. B. C. D.
7.△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于点D,下列四个选项中,错误的是( )
A.sin α=cos α B.tan C=2 C.sin β=cos β D.tan α=1
8.如图,在△ABC中,∠ACB=90°,已知∠B=α,∠ADC=β,AB=a,则BD的长可表示为( )
A.a·(cos α-cos β) B.
C.a·cos α- D.a·cos α-asin α·a·tan β
9.如图,传送带和地面所成斜坡AB的坡度为1∶2,物体从地面沿着该斜坡前进了10米,那么物体离地面的高度为( )
A.5 米 B.5 米 C.2 米 D.4 米
10.如图,△ABC中,AB=AC=10,tan A=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是( )
A.2 B.4 C.5 D.10
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,某山坡的坡度为i=1∶,小辰从山脚A出发,沿山坡向上走了200米到达点B,则小辰上升了 米.
12.如图,四边形ABCD的对角线AC,BD相交于点O,且BD平分AC.若BD=8,AC=6,∠BOC=120°,则四边形ABCD的面积为 .(结果保留根号)
13.如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行 小时即可到达.(结果保留根号)
14.一般地,当α,β为任意角时,sin(α+β)与sin(α-β)的值可以用下面的公式求得:sin(α+β)=sin α·cos β+cos α·sin β;sin(α-β)=sin α·cos β-cos α·sin β.例如sin 90°=sin(60°+30°)=sin 60°·cos 30°+cos 60°·sin 30°=×+×=1.则类似地,可以求得
(1)sin 15°的值是 ;
(2)sin 75°的值是 .
三、(本大题共2小题,每小题8分,满分16分)
15.计算:-cos 30°+sin 45°.
16.如图,已知AB是☉O的直径,CD是弦,且CD⊥AB,BC=6,AC=8,求sin ∠ABD的值.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在△ABC中,∠A=30°,cos B=,AC=6.求AB的长.
18.如图,山顶有一座塔AB,塔高33 m.计划在塔的正下方沿直线CD开通穿山隧道EF.从与E点相距80 m的C处测得A,B的仰角分别为27°,22°,从与F点相距50 m的D处测得A的仰角为45°,求隧道EF的长度.(参考数据:tan 22°≈0.40,tan 27°≈0.51)
五、(本大题共2小题,每小题10分,满分20分)
19.如图,某数学活动小组为测量学校旗杆AB的高度,从旗杆正前方2米处的点C出发,沿斜面坡度i=1∶的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A,B,C,D,E在同一平面内,AB⊥BC,AB∥DE.求旗杆AB的高度.(结果保留根号,参考数据:sin 37°≈,cos 37°≈,tan 37°≈)
20.如图,某海监船以60海里/小时的速度从A处出发沿正西方向巡逻,一艘可疑船只在A的西北方向的C处,海监船航行1.5小时到达B处时接到报警,需巡査此可疑船只,此时可疑船只仍在B的北偏西30°方向的C处,然后,可疑船只以一定速度向正西方向逃离,海监船立刻加速以90海里/小时的速度追击,在D处海监船追到可疑船只,D在B的北偏西60°方向.(结果保留根号)
(1)求B,C两处之间的距离;
(2)求海监船追到可疑船只所用的时间.
六、(本题满分12分)
21.如图,已知△ABC中,∠ACB=90°,D是边AB的中点,P是边AC上一动点,BP与CD相交于点E.
(1)如果BC=6,AC=8,且P为AC的中点,求线段BE的长;
(2)连接PD,如果PD⊥AB,且CE=2,ED=3,求cos A的值.
七、(本题满分12分)
22.对于钝角α,定义它的三角函数值如下:
sin α=sin(180°-α),cos α=-cos(180°-α).
(1)求sin 120°,cos 120°,sin 150°的值;
(2)若一个三角形的三个内角的比是1∶1∶4,A,B是这个三角形的两个顶点,sin A,cos B是方程4x2-mx-1=0的两个不相等的实数根,求m的值及∠A,∠B的大小.
八、(本题满分14分)
23.将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2,P是AC上的一个动点.
(1)当点P运动到∠ABC的平分线上时,连接DP,求DP的长;
(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;
(3)当点P运动到什么位置时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上 求出此时 DPBQ的面积.
参 考 答 案
1.D 2.D 3.C 4.A 5.A 6.D 7.C 8.C 9.C 10.B
11.100 12.12 13. 14.(1) (2)
15.解:原式=-×+×=-+1=0.
16.解:由条件可知∠ABD=∠ABC,∵AB为☉O的直径,∴∠ACB=90°,又∵BC=6,AC=8,∴AB=10,∴sin ∠ABD=sin ∠ABC==.
17.解:过点C作CD⊥AB于点D.∵∠A=30°,∴CD=AC=3,AD=AC·cos A=9.在Rt△BCD中,设BD=4x,∴BC=5x.由勾股定理得CD=3x.由题意得3x=3,解得x=,∴BD=4,∴AB=AD+BD=9+4.
18.解:延长AB交CD于点H,∴AH⊥CD.在Rt△AHD中,∠D=45°,∴AH=DH.在Rt△AHC中,AH=CH·tan ∠ACH≈0.51CH.在Rt△BHC中,BH=CH·tan ∠BCH≈0.4CH,由题意得0.51CH-0.4CH=33,解得CH=300,∴EH=CH-CE=220,BH=120,∴AH=AB+BH=153,∴DH=AH=153,∴HF=DH-DF=103,∴EF=EH+FH=323.答:隧道EF的长度约为323 m.
19.解:延长ED交BC的延长线于点F,∴∠CFD=90°.∵tan ∠DCF=i==,∴∠DCF=30°.∵CD=4,∴DF=2,CF=CD·cos ∠DCF=2,∴BF=BC+CF=2+2=4.过点E作EG⊥AB于点G,∴GE=BF=4,GB=EF=ED+DF=3.5.又∵∠AEG=37°,∴AG=GE·tan ∠AEG=4·tan 37°,∴AB=AG+BG=4·tan 37°+3.5≈3+3.5,答:旗杆AB的高度约为(3+3.5)米.
20.解:(1)过点C作CE⊥AB于点E,则∠CEA=90°,∠CBE=60°.由题意得AB=60×1.5=90,∠CAB=45°,∴△ACE是等腰直角三角形.∴CE=AE,CE=BE,BC=2BE.设BE=x,则CE=x,AE=BE+AB=x+90,∴x=x+90,解得x=45+45,∴BC=2x=90+90.答:B,C两处之间的距离为(90+90)海里.
(2)过点D作DF⊥AB,交AB的延长线于点F,∴DF=CE=x=135+45,∠DBF=90°-60°=30°,∴BD=2DF=270+90,∴海监船追到可疑船只所用的时间为=(3+)小时.答:海监船追到可疑船只所用的时间为(3+)小时.
21.解:(1)∵P为AC的中点,AC=8,∴CP=4.∵∠ACB=90°,BC=6,∴BP=2.∵D是边AB的中点,P为AC的中点,∴点E是△ABC的重心,∴BE=BP=.
(2)如图,过点B作BF∥CA,交CD的延长线于点F,∴==.∵BD=DA,∴FD=DC,BF=AC.∵CE=2,ED=3,∴CD=5,∴EF=8,∴===,∴=,∴=.设CP=k,∴PA=3k.∵PD⊥AB,D是边AB的中点,∴PA=PB=3k,∴BC=2k,∴AB=2k.∵AC=4k,∴cos A=.
22.解:(1)由题意得sin 120°=sin(180°-120°)=sin 60°=,cos 120°=-cos(180°-120°)=-cos 60°=-,sin 150°=sin(180°-150°)=sin 30°=.
(2)∵三角形的三个内角的比是1∶1∶4,∴三个内角分别为30°,30°,120°.①当∠A=30°,∠B=120°时,方程的两根为,-,将x=代入方程,得4×()2-m×-1=0,解得m=0,经检验,-是方程4x2-1=0的根,∴m=0符合题意;②当∠A=120°,∠B=30°时,方程的两根为,,不符合题意;③当∠A=30°,∠B=30°时,方程的两根为,,将x=代入方程,得4×()2-m×-1=0,解得m=0,经检验,不是方程4x2-1=0的根,不符合题意.综上可知m=0,∠A=30°,∠B=120°.
23.解:在Rt△ABC中,AB=2,∠BAC=30°,∴BC=,AC=3.
(1)如图1,作DF⊥AC.∵Rt△ACD中,AD=CD,∴DF=AF=CF=.∵BP平分∠ABC,∴∠PBC=30°,∴CP=BC·tan 30°=1,∴PF=,∴DP==.
(2)当点P位置如图2所示时,根据(1)中结论,DF=,∠ADF=45°.又∵PD=BC=,∴cos ∠PDF==,∴∠PDF=30°,∴∠PDA=∠ADF-∠PDF=15°.当点P位置如图3所示时,同理得∠PDF=30°.∴∠PDA=∠ADF+∠PDF=75°.故∠PDA的度数为15°或75°.
(3)当点P运动到边AC的中点(如图4),即CP=时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上.∵四边形DPBQ为平行四边形,∴BC∥DP.∵∠ACB=90°,∴∠DPC=90°,即DP⊥AC.又∵在Rt△ABC中,AB=2,BC=,∴根据勾股定理得AC=3.∵△ACD为等腰直角三角形,∴DP=CP=AC=,∵BC∥DP,∴PC是平行四边形DPBQ的高,∴S DPBQ=DP·CP=.
1 / 10
