人教版数学八年级上册 周末培优五 (13.3-13.4)(含答案)
文档属性
| 名称 | 人教版数学八年级上册 周末培优五 (13.3-13.4)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 23:45:38 | ||
图片预览




文档简介
人教版数学八年级上册 周末培优五
(范围:13.3-13.4)
一、选择题
1.(2022·泰安)如图,l1∥l2,点A在直线l1上,点B在直线l2上,AB=BC,∠C=25°,∠1=60°.则∠2的度数是( )
A.70° B.65° C.60° D.55°
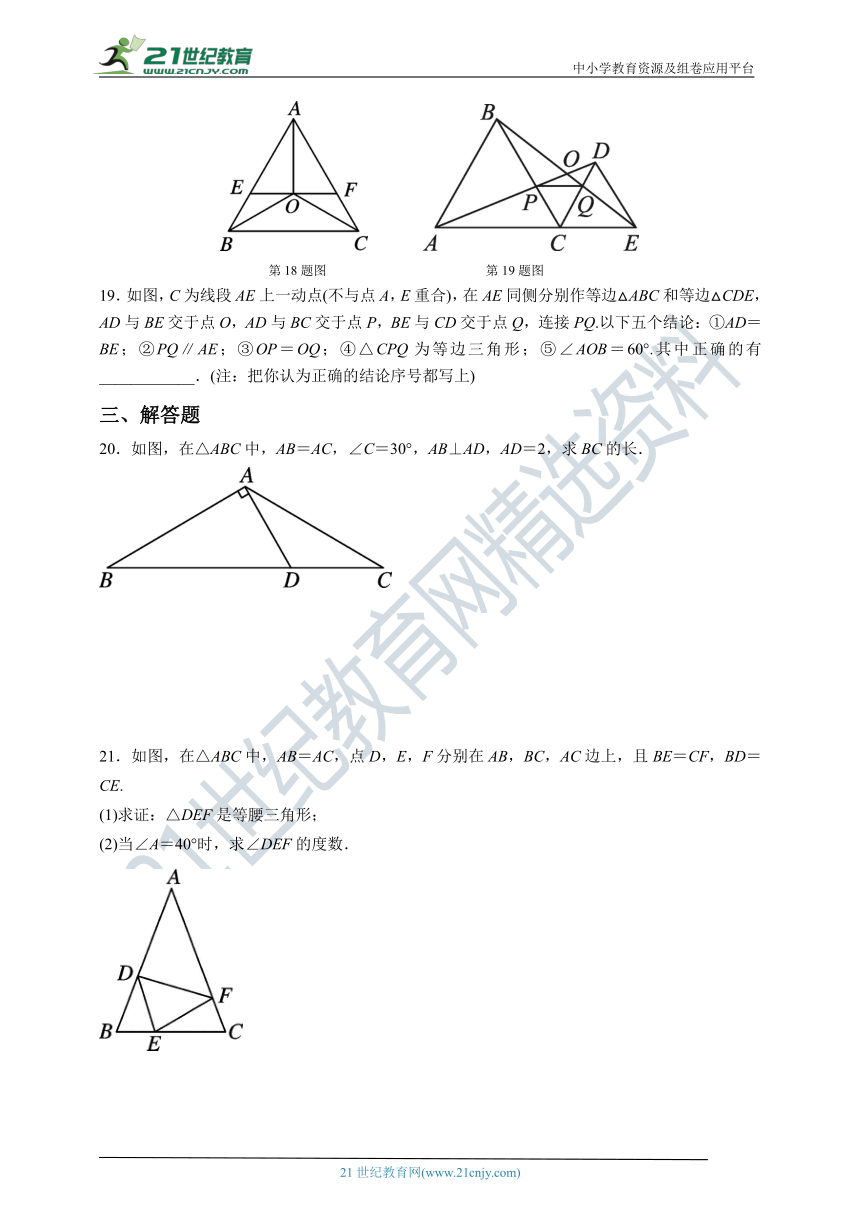
第1题图 第2题图 第5题图
2.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( )
A.50° B.70° C.75° D.80°
3.在Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2cm,则AB的长度是( )
A.2cm B.4cm C.8cm D.16cm
4.等边三角形的三条对称轴中任意两条夹角(锐角)的度数为( )
A.30° B.45° C.60° D.75°
5.如图,将一张长方形纸片ABCD按图中方式折叠,若AE=3,AB=4,BE=5,则重叠部分的面积为( )
A.6 B.8 C.10 D.12
6.如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB等于( )
A.40° B.30° C.20° D.15°
第6题图 第10题图 第12题图
7.在△ABC中,AB=AC,∠B=36°,D、E是边BC上的两点,且∠ADE=∠AED=2∠BAD,则∠DAE的度数为( )
A.56° B.36° C.72° D.不能确定
8.∠AOB的边OA上有两点M、N,在∠AOB的平分线OC上找一点P,使MP+NP最小,正确的作法是( )
9.如图,下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( )
A.①②③ B.①②④ C.②③④ D.①③④
10.如图,在等腰△ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD=( )
A. B. C.a-b D.b-a
11.在平面直角坐标系xOy中,已知点P(2,2),点Q在y轴上,△PQO是等腰三角形,则满足条件的点Q共有( )
A.5个 B.4个 C.3个 D.2个
12.如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是( )
A.平行 B.相交 C.垂直 D.平行、相交或垂直
二、填空题
13.如果等腰三角形的一个内角等于110°,则它的两个底角都是________°.
14.如图,AB∥CD,EF交AB于点H,交CD于点G,连接AG,若AG=HG,∠1=48°,则∠A=_________.
第14题图 第15题图 第17题图
15.根据如图作图痕迹可计算出∠BOC等于_________.
16.等腰三角形的顶角为30°,腰长为4 cm,则三角形的面积是____________.
17.如图,在△ABC中,AB=AC,点E在CA的延长线上,ED⊥BC于点D,交AB于点F,若AF=2,BF=3,则CE的长为___.
18.如图,等边三角形ABC的三条角平分线相交于点O,过点O作EF∥BC分别交AB,AC于点E,F,则图中的等腰三角形有___个.
第18题图 第19题图
19.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③OP=OQ;④△CPQ为等边三角形;⑤∠AOB=60°.其中正确的有____________.(注:把你认为正确的结论序号都写上)
三、解答题
20.如图,在△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=2,求BC的长.
21.如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数.
22.如图,△ABC是边长为12 cm的等边三角形,动点M,N同时从A,B两点出发,分别沿AB,BC方向匀速移动.
(1)若点M,N的运动速度是2 cm/s,4 cm/s,当点N到达点C时,M,N两点都停止运动,设运动时间为t(s),当t=2时,判断△BMN的形状,并说明理由;
(2)当它们的运动速度都是2 cm/s,且当点M到达点B时,M,N两点停止运动,设点M的运动时间为t(s),则当t为何值时,△MBN是直角三角形?
23.如图,△ABC是边长为9的等边三角形,P是AC边上一动点,由A向C运动(与A,C不重合),H是CB延长线上的一动点,与点P同时以相同的速度由B向CB延长线方向运动(H不与B重合),过P作PE⊥AB与E,连接PH交AB于D.
(1)当∠BHD=30°时,求AP的长;
(2)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果发生变化,请说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.(2022·泰安)如图,l1∥l2,点A在直线l1上,点B在直线l2上,AB=BC,∠C=25°,∠1=60°.则∠2的度数是( A )
A.70° B.65° C.60° D.55°
第1题图 第2题图 第5题图
2.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( B )
A.50° B.70° C.75° D.80°
3.在Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2cm,则AB的长度是( C )
A.2cm B.4cm C.8cm D.16cm
4.等边三角形的三条对称轴中任意两条夹角(锐角)的度数为( C )
A.30° B.45° C.60° D.75°
5.如图,将一张长方形纸片ABCD按图中方式折叠,若AE=3,AB=4,BE=5,则重叠部分的面积为( C )
A.6 B.8 C.10 D.12
6.如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB等于( C )
A.40° B.30° C.20° D.15°
第6题图 第10题图 第12题图
7.在△ABC中,AB=AC,∠B=36°,D、E是边BC上的两点,且∠ADE=∠AED=2∠BAD,则∠DAE的度数为( B )
A.56° B.36° C.72° D.不能确定
8.∠AOB的边OA上有两点M、N,在∠AOB的平分线OC上找一点P,使MP+NP最小,正确的作法是( D )
9.如图,下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( D )
A.①②③ B.①②④ C.②③④ D.①③④
10.如图,在等腰△ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD=( C )
A. B. C.a-b D.b-a
11.在平面直角坐标系xOy中,已知点P(2,2),点Q在y轴上,△PQO是等腰三角形,则满足条件的点Q共有( B )
A.5个 B.4个 C.3个 D.2个
12.如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是( A )
A.平行 B.相交 C.垂直 D.平行、相交或垂直
二、填空题
13.如果等腰三角形的一个内角等于110°,则它的两个底角都是________°.
【答案】35
14.如图,AB∥CD,EF交AB于点H,交CD于点G,连接AG,若AG=HG,∠1=48°,则∠A=_________.
【答案】48°
第14题图 第15题图 第17题图
15.根据如图作图痕迹可计算出∠BOC等于_________.
【答案】30°
16.等腰三角形的顶角为30°,腰长为4 cm,则三角形的面积是____________.
【答案】4 cm2
17.如图,在△ABC中,AB=AC,点E在CA的延长线上,ED⊥BC于点D,交AB于点F,若AF=2,BF=3,则CE的长为___.
【答案】7
18.如图,等边三角形ABC的三条角平分线相交于点O,过点O作EF∥BC分别交AB,AC于点E,F,则图中的等腰三角形有___个.
【答案】12
第18题图 第19题图
19.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③OP=OQ;④△CPQ为等边三角形;⑤∠AOB=60°.其中正确的有____________.(注:把你认为正确的结论序号都写上)
【答案】①②④⑤
三、解答题
20.如图,在△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=2,求BC的长.
解:∵AB=AC,∠C=30°,
∴∠B=∠C=30°.
∴∠BAC=120°.
∵AB⊥AD,∴∠BAD=90°.
∴∠DAC=120°-90°=30°=∠C.
∴AD=CD=2.
∵AB⊥AD,∠B=30°,
∴BD=2AD=4.
∴BC=BD+CD=6.
21.如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数.
解:(1)证明:∵AB=AC,
∴∠B=∠C.
在△DBE和△ECF中,
∴△DBE≌△ECF,∴DE=EF,
∴△DEF是等腰三角形.
(2)∵△DBE≌△ECF,
∴∠1=∠3,∠2=∠4.
∵∠A+∠B+∠C=180°,∠B=∠C,∠A=40°,
∴∠B=70°,
∴∠1+∠2=110°,
∴∠3+∠2=110°,
∴∠DEF=70°.
22.如图,△ABC是边长为12 cm的等边三角形,动点M,N同时从A,B两点出发,分别沿AB,BC方向匀速移动.
(1)若点M,N的运动速度是2 cm/s,4 cm/s,当点N到达点C时,M,N两点都停止运动,设运动时间为t(s),当t=2时,判断△BMN的形状,并说明理由;
(2)当它们的运动速度都是2 cm/s,且当点M到达点B时,M,N两点停止运动,设点M的运动时间为t(s),则当t为何值时,△MBN是直角三角形?
解:(1)△BMN是等边三角形.
理由:当t=2时,AM=4 cm,BN=8 cm.
∵△ABC是等边三角形且边长是12 cm,
∴BM=8 cm,∠B=60°,
∴BM=BN,
∴△BMN是等边三角形.
(2)在△BMN中,BM=(12-2t) cm,BN=2t cm.
①若∠BNM=90°,则∠BMN=30°,
∴BN=BM,
∴2t=(12-2t),解得t=2;
②若∠BMN=90°,则∠BNM=30°,
∴BM=BN,
∴12-2t=×2t,解得t=4.
综上所述,当t=2 s或t=4 s时,△MBN是直角三角形.
23.如图,△ABC是边长为9的等边三角形,P是AC边上一动点,由A向C运动(与A,C不重合),H是CB延长线上的一动点,与点P同时以相同的速度由B向CB延长线方向运动(H不与B重合),过P作PE⊥AB与E,连接PH交AB于D.
(1)当∠BHD=30°时,求AP的长;
解:当∠BHD=30°时,易证HB=DB=AP.设AP=x,AD=2x,
所以x+2x=9,解得x=3,即AP=3.
(2)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果发生变化,请说明理由.
解:不发生变化.
过点H作HF⊥AB的延长线于点F,
易证△HFB≌△PEA,△DEP≌△DFH,
所以得DE=DF=AB=.
(范围:13.3-13.4)
一、选择题
1.(2022·泰安)如图,l1∥l2,点A在直线l1上,点B在直线l2上,AB=BC,∠C=25°,∠1=60°.则∠2的度数是( )
A.70° B.65° C.60° D.55°
第1题图 第2题图 第5题图
2.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( )
A.50° B.70° C.75° D.80°
3.在Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2cm,则AB的长度是( )
A.2cm B.4cm C.8cm D.16cm
4.等边三角形的三条对称轴中任意两条夹角(锐角)的度数为( )
A.30° B.45° C.60° D.75°
5.如图,将一张长方形纸片ABCD按图中方式折叠,若AE=3,AB=4,BE=5,则重叠部分的面积为( )
A.6 B.8 C.10 D.12
6.如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB等于( )
A.40° B.30° C.20° D.15°
第6题图 第10题图 第12题图
7.在△ABC中,AB=AC,∠B=36°,D、E是边BC上的两点,且∠ADE=∠AED=2∠BAD,则∠DAE的度数为( )
A.56° B.36° C.72° D.不能确定
8.∠AOB的边OA上有两点M、N,在∠AOB的平分线OC上找一点P,使MP+NP最小,正确的作法是( )
9.如图,下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( )
A.①②③ B.①②④ C.②③④ D.①③④
10.如图,在等腰△ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD=( )
A. B. C.a-b D.b-a
11.在平面直角坐标系xOy中,已知点P(2,2),点Q在y轴上,△PQO是等腰三角形,则满足条件的点Q共有( )
A.5个 B.4个 C.3个 D.2个
12.如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是( )
A.平行 B.相交 C.垂直 D.平行、相交或垂直
二、填空题
13.如果等腰三角形的一个内角等于110°,则它的两个底角都是________°.
14.如图,AB∥CD,EF交AB于点H,交CD于点G,连接AG,若AG=HG,∠1=48°,则∠A=_________.
第14题图 第15题图 第17题图
15.根据如图作图痕迹可计算出∠BOC等于_________.
16.等腰三角形的顶角为30°,腰长为4 cm,则三角形的面积是____________.
17.如图,在△ABC中,AB=AC,点E在CA的延长线上,ED⊥BC于点D,交AB于点F,若AF=2,BF=3,则CE的长为___.
18.如图,等边三角形ABC的三条角平分线相交于点O,过点O作EF∥BC分别交AB,AC于点E,F,则图中的等腰三角形有___个.
第18题图 第19题图
19.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③OP=OQ;④△CPQ为等边三角形;⑤∠AOB=60°.其中正确的有____________.(注:把你认为正确的结论序号都写上)
三、解答题
20.如图,在△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=2,求BC的长.
21.如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数.
22.如图,△ABC是边长为12 cm的等边三角形,动点M,N同时从A,B两点出发,分别沿AB,BC方向匀速移动.
(1)若点M,N的运动速度是2 cm/s,4 cm/s,当点N到达点C时,M,N两点都停止运动,设运动时间为t(s),当t=2时,判断△BMN的形状,并说明理由;
(2)当它们的运动速度都是2 cm/s,且当点M到达点B时,M,N两点停止运动,设点M的运动时间为t(s),则当t为何值时,△MBN是直角三角形?
23.如图,△ABC是边长为9的等边三角形,P是AC边上一动点,由A向C运动(与A,C不重合),H是CB延长线上的一动点,与点P同时以相同的速度由B向CB延长线方向运动(H不与B重合),过P作PE⊥AB与E,连接PH交AB于D.
(1)当∠BHD=30°时,求AP的长;
(2)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果发生变化,请说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.(2022·泰安)如图,l1∥l2,点A在直线l1上,点B在直线l2上,AB=BC,∠C=25°,∠1=60°.则∠2的度数是( A )
A.70° B.65° C.60° D.55°
第1题图 第2题图 第5题图
2.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( B )
A.50° B.70° C.75° D.80°
3.在Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2cm,则AB的长度是( C )
A.2cm B.4cm C.8cm D.16cm
4.等边三角形的三条对称轴中任意两条夹角(锐角)的度数为( C )
A.30° B.45° C.60° D.75°
5.如图,将一张长方形纸片ABCD按图中方式折叠,若AE=3,AB=4,BE=5,则重叠部分的面积为( C )
A.6 B.8 C.10 D.12
6.如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB等于( C )
A.40° B.30° C.20° D.15°
第6题图 第10题图 第12题图
7.在△ABC中,AB=AC,∠B=36°,D、E是边BC上的两点,且∠ADE=∠AED=2∠BAD,则∠DAE的度数为( B )
A.56° B.36° C.72° D.不能确定
8.∠AOB的边OA上有两点M、N,在∠AOB的平分线OC上找一点P,使MP+NP最小,正确的作法是( D )
9.如图,下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( D )
A.①②③ B.①②④ C.②③④ D.①③④
10.如图,在等腰△ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD=( C )
A. B. C.a-b D.b-a
11.在平面直角坐标系xOy中,已知点P(2,2),点Q在y轴上,△PQO是等腰三角形,则满足条件的点Q共有( B )
A.5个 B.4个 C.3个 D.2个
12.如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是( A )
A.平行 B.相交 C.垂直 D.平行、相交或垂直
二、填空题
13.如果等腰三角形的一个内角等于110°,则它的两个底角都是________°.
【答案】35
14.如图,AB∥CD,EF交AB于点H,交CD于点G,连接AG,若AG=HG,∠1=48°,则∠A=_________.
【答案】48°
第14题图 第15题图 第17题图
15.根据如图作图痕迹可计算出∠BOC等于_________.
【答案】30°
16.等腰三角形的顶角为30°,腰长为4 cm,则三角形的面积是____________.
【答案】4 cm2
17.如图,在△ABC中,AB=AC,点E在CA的延长线上,ED⊥BC于点D,交AB于点F,若AF=2,BF=3,则CE的长为___.
【答案】7
18.如图,等边三角形ABC的三条角平分线相交于点O,过点O作EF∥BC分别交AB,AC于点E,F,则图中的等腰三角形有___个.
【答案】12
第18题图 第19题图
19.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③OP=OQ;④△CPQ为等边三角形;⑤∠AOB=60°.其中正确的有____________.(注:把你认为正确的结论序号都写上)
【答案】①②④⑤
三、解答题
20.如图,在△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=2,求BC的长.
解:∵AB=AC,∠C=30°,
∴∠B=∠C=30°.
∴∠BAC=120°.
∵AB⊥AD,∴∠BAD=90°.
∴∠DAC=120°-90°=30°=∠C.
∴AD=CD=2.
∵AB⊥AD,∠B=30°,
∴BD=2AD=4.
∴BC=BD+CD=6.
21.如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数.
解:(1)证明:∵AB=AC,
∴∠B=∠C.
在△DBE和△ECF中,
∴△DBE≌△ECF,∴DE=EF,
∴△DEF是等腰三角形.
(2)∵△DBE≌△ECF,
∴∠1=∠3,∠2=∠4.
∵∠A+∠B+∠C=180°,∠B=∠C,∠A=40°,
∴∠B=70°,
∴∠1+∠2=110°,
∴∠3+∠2=110°,
∴∠DEF=70°.
22.如图,△ABC是边长为12 cm的等边三角形,动点M,N同时从A,B两点出发,分别沿AB,BC方向匀速移动.
(1)若点M,N的运动速度是2 cm/s,4 cm/s,当点N到达点C时,M,N两点都停止运动,设运动时间为t(s),当t=2时,判断△BMN的形状,并说明理由;
(2)当它们的运动速度都是2 cm/s,且当点M到达点B时,M,N两点停止运动,设点M的运动时间为t(s),则当t为何值时,△MBN是直角三角形?
解:(1)△BMN是等边三角形.
理由:当t=2时,AM=4 cm,BN=8 cm.
∵△ABC是等边三角形且边长是12 cm,
∴BM=8 cm,∠B=60°,
∴BM=BN,
∴△BMN是等边三角形.
(2)在△BMN中,BM=(12-2t) cm,BN=2t cm.
①若∠BNM=90°,则∠BMN=30°,
∴BN=BM,
∴2t=(12-2t),解得t=2;
②若∠BMN=90°,则∠BNM=30°,
∴BM=BN,
∴12-2t=×2t,解得t=4.
综上所述,当t=2 s或t=4 s时,△MBN是直角三角形.
23.如图,△ABC是边长为9的等边三角形,P是AC边上一动点,由A向C运动(与A,C不重合),H是CB延长线上的一动点,与点P同时以相同的速度由B向CB延长线方向运动(H不与B重合),过P作PE⊥AB与E,连接PH交AB于D.
(1)当∠BHD=30°时,求AP的长;
解:当∠BHD=30°时,易证HB=DB=AP.设AP=x,AD=2x,
所以x+2x=9,解得x=3,即AP=3.
(2)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果发生变化,请说明理由.
解:不发生变化.
过点H作HF⊥AB的延长线于点F,
易证△HFB≌△PEA,△DEP≌△DFH,
所以得DE=DF=AB=.
