人教版数学九年级下册 29.2三视图学案(无答案)
文档属性
| 名称 | 人教版数学九年级下册 29.2三视图学案(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 382.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-11 14:03:59 | ||
图片预览


文档简介
三视图
【学习目标】
1.了解视图的概念,明确视图与投影的关系。
2.理解三视图中主视图、左视图、俯视图的概念,明确三视图与我们从三个方向看物体所得到的图象的联系与区别,会画立体图形的三视图。
3.画三视图时,要使主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等。
4.掌握由三视图想象出立体图形的方法,以及在实际中的运用。
【学习重难点】
1.了解视图的概念,明确视图与投影的关系。
2.理解三视图中主视图、左视图、俯视图的概念,明确三视图与我们从三个方向看物体所得到的图象的联系与区别,会画立体图形的三视图。
3.掌握由三视图想象出立体图形的方法,以及在实际中的运用。
【学习过程】
一、自主预习。
阅读教材本小节,弄清楚视图、主视图、俯视图、左视图的概念,以及画三视图时的位置和视图之间的大小关系。
1.出示学习成果。
①当我们从某一角度观察一个物体时,所看到的图象叫做物体的一个____________,也可以看作物体在某一角度的光线下的__________。
②主视图是在正面内得到的由________向________观察物体的视图;俯视图是在水平面内得到的由_________向___________观察物体的视图;左视图是在侧面内得到的由_________向__________观察物体的视图。
③主视图与俯视图的_________对正,主视图与左视图的_______平齐,左视图与俯视图的宽_______。
④三视图一般规定主视图要在____________,俯视图在_________,左视图在___________,其中主视图反映物体的_________和__________,左视图反映物体的_________和__________,俯视图反映物体的_________和______。
二、合作探究。
1.小组讨论。
画出如图所示一些基本几何体的三视图。
2.跟踪训练。
①主视图、俯视图、左视图分别反映物体哪些长度特征?
②画出半球和圆锥的三视图。
3.画出如图所示的支架(一种小零件)的三视图,支架的两个台阶的高度和宽度都是同一长度。
4.跟踪训练(小组讨论完成后展示学习成果)。
①一个几何体的主视图、俯视图、左视图都是正方形,那么这个几何体可能是__________。
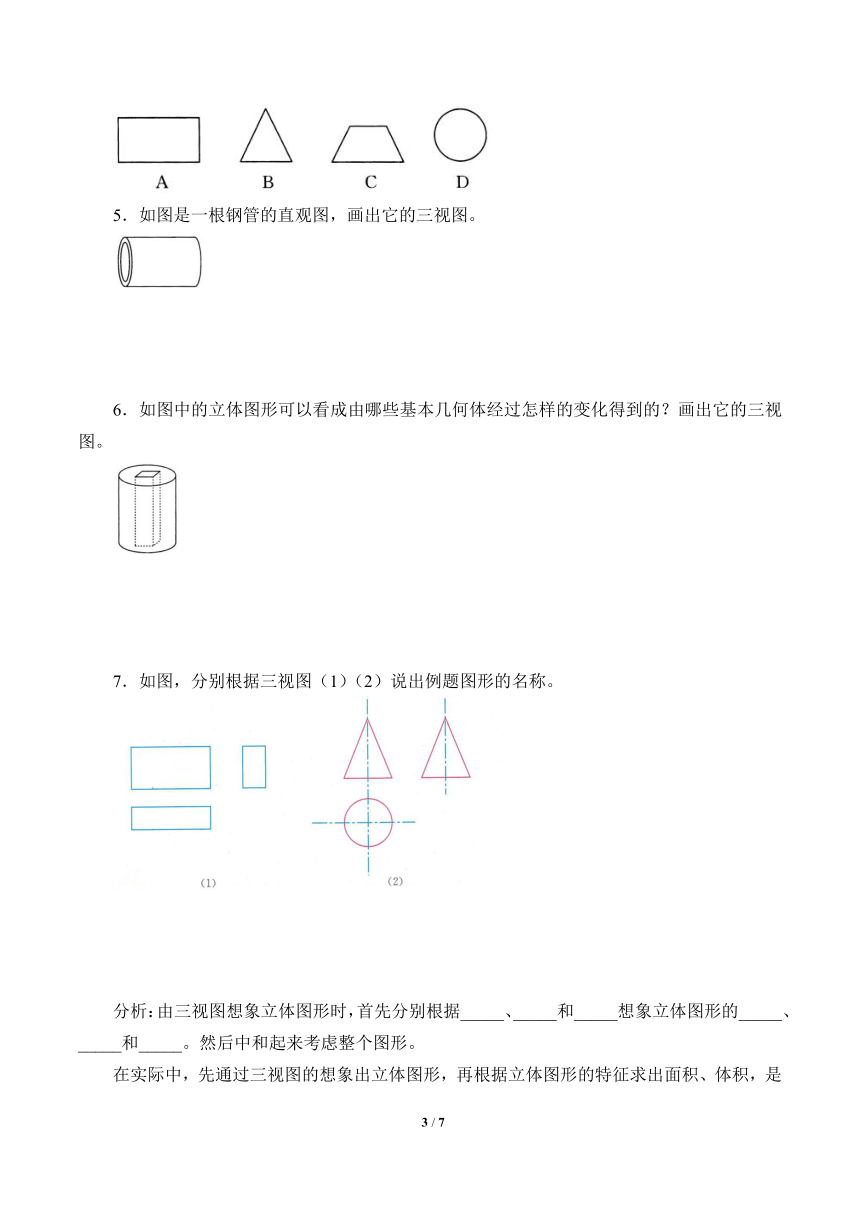
②下列图中能表示一个圆台的主视图的是( )。
5.如图是一根钢管的直观图,画出它的三视图。
6.如图中的立体图形可以看成由哪些基本几何体经过怎样的变化得到的?画出它的三视图。
7.如图,分别根据三视图(1)(2)说出例题图形的名称。
分析:由三视图想象立体图形时,首先分别根据_____、_____和_____想象立体图形的_____、_____和_____。然后中和起来考虑整个图形。
在实际中,先通过三视图的想象出立体图形,再根据立体图形的特征求出面积、体积,是三视图在实际生活中的应用。
练习:某工厂要加工一批密封罐,设计者给出了密封罐的三视图。请按照三视图确定制作每个密封罐所需钢板的面积(图中尺寸单位:mm)。
三、当堂反馈。
1.如图,桌面上有一个一次性纸杯,它的主视图应是( )。
2.如图所示的支架是由两个长方体构成的组合体,则它的主视图是( )。
3.如图,图中的几何体是圆柱沿竖起方向切掉一半后得到的,则该几何体的俯视图是( )。
4.如图的立体图形的左视图可能是( )。
5.如图是由5个大小相同的正方体组成的几何体,它的主视图是( )。
6.画出几何体的三视图。
四、拓展提升。
中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池。类似地,有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为下面几何体中的哪一个?选择并说明理由。
五、课后检测。
1.下列立体图形中,俯视图是正方形的是( )。
2.如图是由4个大小相同的正方体搭成的几何体,其俯视图是( )。
3.下列几何体,主视图和俯视图都为矩形的是( )。
4.6月15日“父亲节”,小明送给父亲一个礼盒(如图),该礼盒的主视图是( )。
5.下图是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所示数字为该处小正方体的个数,则这个几何体的左视图是( )。
6.写出一个在三视图中俯视图与主视图完全相同的几何体:_______。
7.一位美术老师在课堂上进行立体模型素描教学时,把由圆锥与圆柱组成的几何体(如图所示,圆锥在圆柱上底面正中间放置)摆在讲桌上,请你在指定的方框内分别画出这个几何体的三视图(从正面、左面、上面看到的视图)。
8.一种机器上有一个进行转动的零件叫燕尾槽(如图),为了准确做出这个零件,请画出它的三视图。
7 / 7
【学习目标】
1.了解视图的概念,明确视图与投影的关系。
2.理解三视图中主视图、左视图、俯视图的概念,明确三视图与我们从三个方向看物体所得到的图象的联系与区别,会画立体图形的三视图。
3.画三视图时,要使主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等。
4.掌握由三视图想象出立体图形的方法,以及在实际中的运用。
【学习重难点】
1.了解视图的概念,明确视图与投影的关系。
2.理解三视图中主视图、左视图、俯视图的概念,明确三视图与我们从三个方向看物体所得到的图象的联系与区别,会画立体图形的三视图。
3.掌握由三视图想象出立体图形的方法,以及在实际中的运用。
【学习过程】
一、自主预习。
阅读教材本小节,弄清楚视图、主视图、俯视图、左视图的概念,以及画三视图时的位置和视图之间的大小关系。
1.出示学习成果。
①当我们从某一角度观察一个物体时,所看到的图象叫做物体的一个____________,也可以看作物体在某一角度的光线下的__________。
②主视图是在正面内得到的由________向________观察物体的视图;俯视图是在水平面内得到的由_________向___________观察物体的视图;左视图是在侧面内得到的由_________向__________观察物体的视图。
③主视图与俯视图的_________对正,主视图与左视图的_______平齐,左视图与俯视图的宽_______。
④三视图一般规定主视图要在____________,俯视图在_________,左视图在___________,其中主视图反映物体的_________和__________,左视图反映物体的_________和__________,俯视图反映物体的_________和______。
二、合作探究。
1.小组讨论。
画出如图所示一些基本几何体的三视图。
2.跟踪训练。
①主视图、俯视图、左视图分别反映物体哪些长度特征?
②画出半球和圆锥的三视图。
3.画出如图所示的支架(一种小零件)的三视图,支架的两个台阶的高度和宽度都是同一长度。
4.跟踪训练(小组讨论完成后展示学习成果)。
①一个几何体的主视图、俯视图、左视图都是正方形,那么这个几何体可能是__________。
②下列图中能表示一个圆台的主视图的是( )。
5.如图是一根钢管的直观图,画出它的三视图。
6.如图中的立体图形可以看成由哪些基本几何体经过怎样的变化得到的?画出它的三视图。
7.如图,分别根据三视图(1)(2)说出例题图形的名称。
分析:由三视图想象立体图形时,首先分别根据_____、_____和_____想象立体图形的_____、_____和_____。然后中和起来考虑整个图形。
在实际中,先通过三视图的想象出立体图形,再根据立体图形的特征求出面积、体积,是三视图在实际生活中的应用。
练习:某工厂要加工一批密封罐,设计者给出了密封罐的三视图。请按照三视图确定制作每个密封罐所需钢板的面积(图中尺寸单位:mm)。
三、当堂反馈。
1.如图,桌面上有一个一次性纸杯,它的主视图应是( )。
2.如图所示的支架是由两个长方体构成的组合体,则它的主视图是( )。
3.如图,图中的几何体是圆柱沿竖起方向切掉一半后得到的,则该几何体的俯视图是( )。
4.如图的立体图形的左视图可能是( )。
5.如图是由5个大小相同的正方体组成的几何体,它的主视图是( )。
6.画出几何体的三视图。
四、拓展提升。
中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池。类似地,有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为下面几何体中的哪一个?选择并说明理由。
五、课后检测。
1.下列立体图形中,俯视图是正方形的是( )。
2.如图是由4个大小相同的正方体搭成的几何体,其俯视图是( )。
3.下列几何体,主视图和俯视图都为矩形的是( )。
4.6月15日“父亲节”,小明送给父亲一个礼盒(如图),该礼盒的主视图是( )。
5.下图是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所示数字为该处小正方体的个数,则这个几何体的左视图是( )。
6.写出一个在三视图中俯视图与主视图完全相同的几何体:_______。
7.一位美术老师在课堂上进行立体模型素描教学时,把由圆锥与圆柱组成的几何体(如图所示,圆锥在圆柱上底面正中间放置)摆在讲桌上,请你在指定的方框内分别画出这个几何体的三视图(从正面、左面、上面看到的视图)。
8.一种机器上有一个进行转动的零件叫燕尾槽(如图),为了准确做出这个零件,请画出它的三视图。
7 / 7
