青岛版八年级数学下册二次根式复习

课件27张PPT。加深理解二次根式的有关概念；熟练掌握二次根式有意义的条件；熟练运用二次根式的化简和加
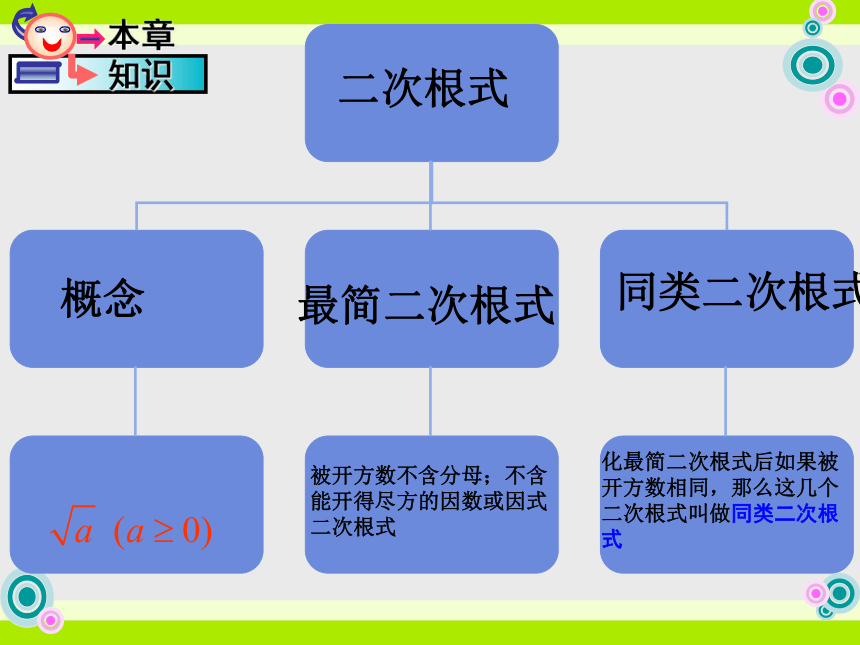
减、乘除、乘方混合运算；复习目标二次根式概念最简二次根式同类二次根式被开方数不含分母；不含
能开得尽方的因数或因式
二次根式化最简二次根式后如果被
开方数相同，那么这几个
二次根式叫做同类二次根式
2.二次根式的性质(1)：（1） 非负性 ：2.二次根式的性质(2)：3.二次根式的运算：二次根式乘法法则二次根式除法法则二次根式的加减： 类似于合并同类项，关键是把同类二次根式合并。二次根式的混合运算： 1.当x取何值时，下列二次根式有意义：①②③④⑤⑥⑦⑧题型1:二次根式有意义的条件2.（2005.吉林）当 _____时， 有意义。 4.求下列二次根式中字母的取值范围≤3a=4说明：二次根式被开方数大于等于0，所以求二次根式中字母的取值范围常转化为不等式(组) 解得若 ，则实数a在数轴上的对应点一定在( )
A、原点左侧
B、原点右侧
C、原点或原点左侧
D、原点或原点右侧C变式训练 ?2.(2005.湖北黄冈市)已知x,y为实数,且
,则 的值为( )
A.3 B.-3 C.1 D.-1题型2:二次根式的非负性的应用D1.已知： ,求 的值.解得解：由题意，得题型3:化简把下列二次根化为最简二次根式变式应用1.式子 成立的条件是（ ） D题型4:同类二次根式BD题型5: 计算9．在实数范围内分解因式（１）（２）（３）（４）设a.b为实数,且求 的值解:

例4练一练 :2.实数a在数轴上的位置如图所示,化简
= .3.若代数式 的值是常数2,则a的取值范围是( )
A. B.
C. D.4、把 根号外的因式移到根号内得

（ ）
5、若化简 的结果是2x-5,
则x的取值范围是（ ） 6. 观察下列分母有理化的计算：
，，，从计算结果中找出规律，并利用这一规律计算：，…，BA. B. C. D.拓展延伸1、试写出下列各式的整数部分和小数部分的整数部分 ，小数部分 。1的整数部分 ，小数部分 。32、化简：3、若a、b分别是 的整数部分和
小数部分2a-b的值是 。细心观察图形,认真分析,思考下列问题.（1）你能求出哪些线段的长？OA2=___
OA3=___
……
OAn=___S1=___
S2=___
……拓展2Sn=___通过这节课的学习，谈谈你的收获。二次根式性质运算作业