23.1 图形的旋转同步练习(无答案)2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 23.1 图形的旋转同步练习(无答案)2023-2024学年人教版九年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 321.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 22:54:38 | ||
图片预览

文档简介
人教版九年级上23.1 图形的旋转
一、选择题
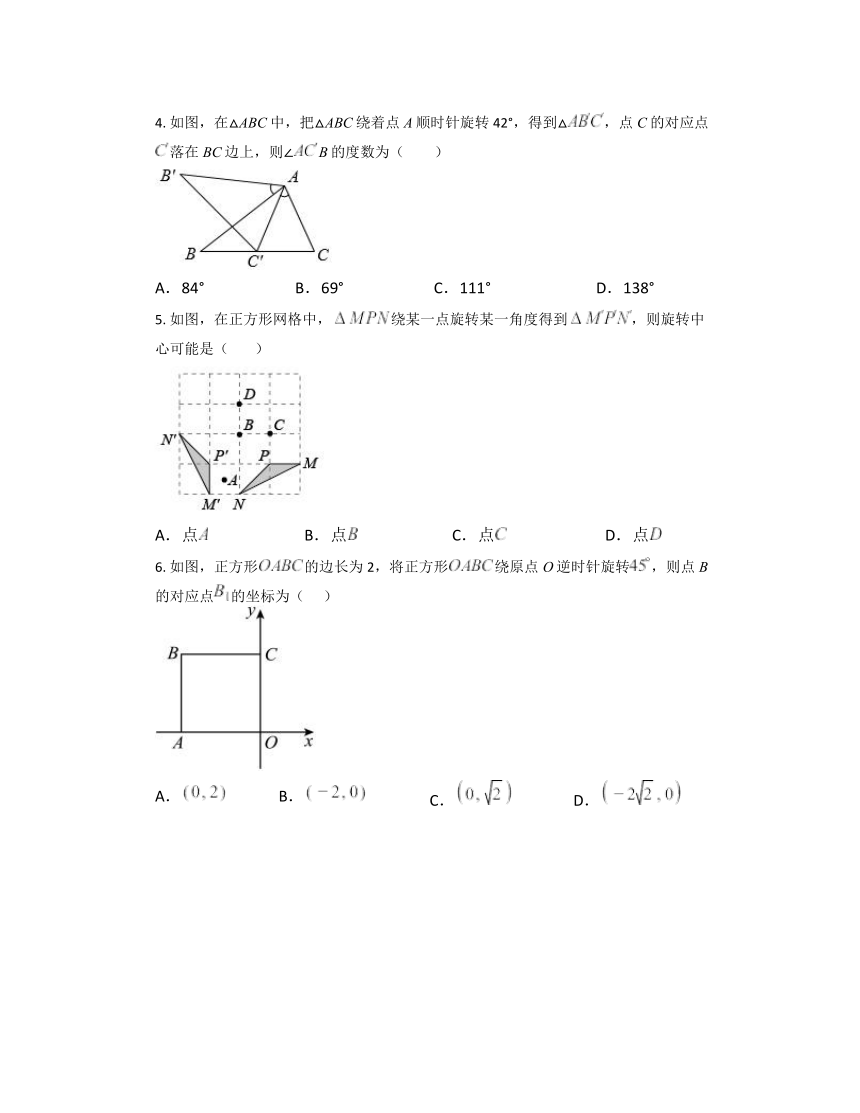
1. 美丽的冬奥雪花呈现出浪漫空灵的气质.如图,雪花图案是一个中心对称图形,也可以看成自身的一部分围绕它的中心依次旋转一定角度得到的,这个角的度数可以是( )
A. B. C. D.
2. 如图,一个小孩坐在秋千上,若秋千绕点旋转了86°,小孩的位置也从点运动到了点,则的度数为( )
A.33° B.37° C.43° D.47°
3. 把图中的图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )
A. B. C. D.
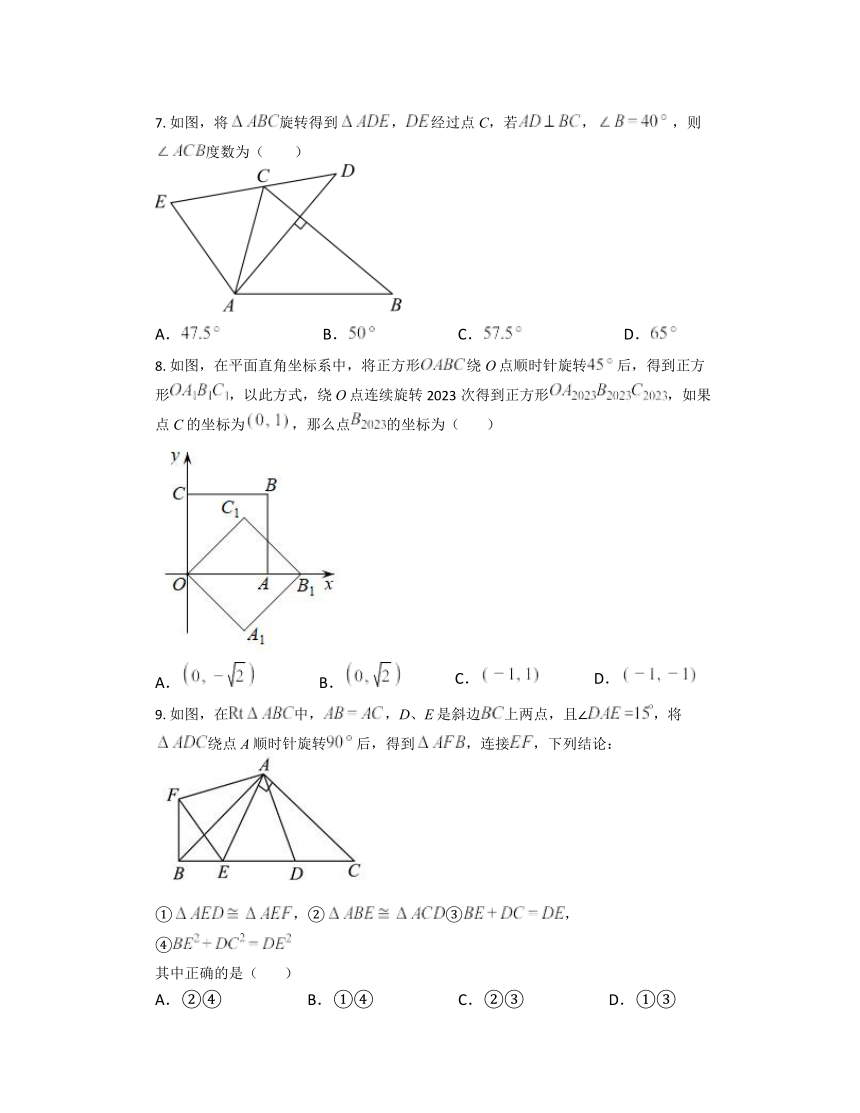
4. 如图,在△ABC中,把△ABC绕着点A顺时针旋转42°,得到△,点C的对应点落在BC边上,则∠B的度数为( )
A.84° B.69° C.111° D.138°
5. 如图,在正方形网格中,绕某一点旋转某一角度得到,则旋转中心可能是( )
A.点 B.点 C.点 D.点
6. 如图,正方形的边长为2,将正方形绕原点O逆时针旋转,则点B的对应点的坐标为( )
A. B. C. D.
7. 如图,将旋转得到,经过点C,若,,则度数为( )
A. B. C. D.
8. 如图,在平面直角坐标系中,将正方形绕O点顺时针旋转后,得到正方形,以此方式,绕O点连续旋转2023次得到正方形,如果点C的坐标为,那么点的坐标为( )
A. B. C. D.
9. 如图,在中,,D、E是斜边上两点,且∠,将绕点A顺时针旋转后,得到,连接,下列结论:
①,②③,④
其中正确的是( )
A.②④ B.①④ C.②③ D.①③
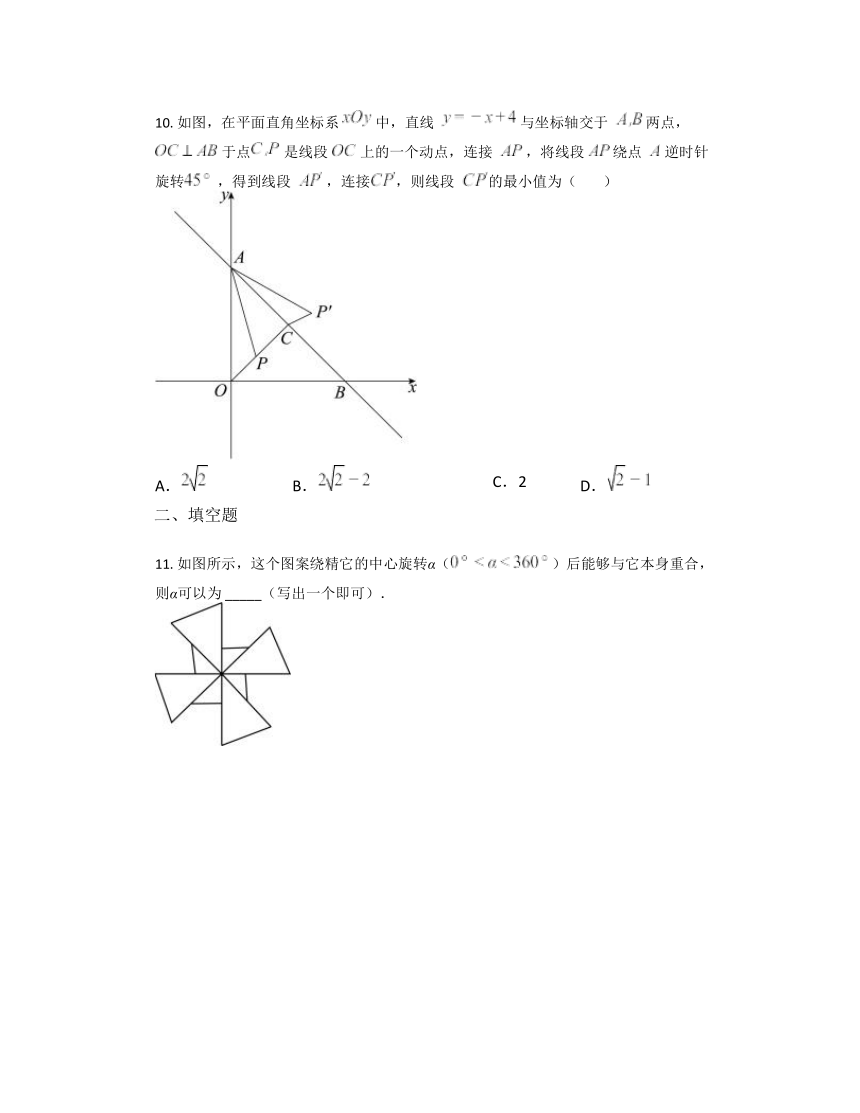
10. 如图,在平面直角坐标系 中,直线 与坐标轴交于 两点, 于点 是线段 上的一个动点,连接 ,将线段 绕点 逆时针旋转 ,得到线段 ,连接,则线段的最小值为( )
A. B. C.2 D.
二、填空题
11. 如图所示,这个图案绕精它的中心旋转α()后能够与它本身重合,则α可以为 _____(写出一个即可).
12. 如图,中,,将绕A点按顺时针旋转,得到,则______.
13. 如图,是边长为的等边三角形,是的中点,是直线上的一个动点,连接,将线段绕点逆时针旋转得到,连接.则在点的运动过程中,的最小值是______.
14. 如图,正方形,点E在上,点F在上,连接,且,则的长为________.
三、解答题
15. (1)解方程:.
(2)如图,将其绕着某点旋转,能与自身重合,求的最小值.
16. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,的三个顶点,,均在格点上.
(1)画出向左平移4个单位得到的,并写出点的坐标;
(2)画出绕点顺时针旋转后得到的,并写出点的坐标.
17. 如图1,抛物线与x轴交于点,两点,与y轴交于点C,经过点B的直线交y轴于点
(1)求抛物线的解析式
(2)如图2,过点A于作的平行线交抛物线于另一点D,点P是抛物线位于线段下方的一个动点,联结,,,,当四边形面积最大时,求点P坐标.
(3)如图3,连接,将绕点O逆时针旋转,记旋转中的三角形为,在旋转的过程中,直线与直线交于点Q,若为等腰三角形,请直接写出点Q的坐标.
18. 【课本再现】把两个全等的矩形和矩形拼成如图1的图案,则______;
【迁移应用】如图2,在正方形中,E是边上一点(不与点C,D重合),连接,将绕点E顺时针旋转至,作射线交的延长线于点G,求证:;
【拓展延伸】在菱形中,,E是边上一点(不与点C,D
重合),连接,将绕点E顺时针旋转至,作射线交的延长线于点G.
①线段与的数量关系是_______.
②若,E是的三等分点,则的面积为_______.
一、选择题
1. 美丽的冬奥雪花呈现出浪漫空灵的气质.如图,雪花图案是一个中心对称图形,也可以看成自身的一部分围绕它的中心依次旋转一定角度得到的,这个角的度数可以是( )
A. B. C. D.
2. 如图,一个小孩坐在秋千上,若秋千绕点旋转了86°,小孩的位置也从点运动到了点,则的度数为( )
A.33° B.37° C.43° D.47°
3. 把图中的图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )
A. B. C. D.
4. 如图,在△ABC中,把△ABC绕着点A顺时针旋转42°,得到△,点C的对应点落在BC边上,则∠B的度数为( )
A.84° B.69° C.111° D.138°
5. 如图,在正方形网格中,绕某一点旋转某一角度得到,则旋转中心可能是( )
A.点 B.点 C.点 D.点
6. 如图,正方形的边长为2,将正方形绕原点O逆时针旋转,则点B的对应点的坐标为( )
A. B. C. D.
7. 如图,将旋转得到,经过点C,若,,则度数为( )
A. B. C. D.
8. 如图,在平面直角坐标系中,将正方形绕O点顺时针旋转后,得到正方形,以此方式,绕O点连续旋转2023次得到正方形,如果点C的坐标为,那么点的坐标为( )
A. B. C. D.
9. 如图,在中,,D、E是斜边上两点,且∠,将绕点A顺时针旋转后,得到,连接,下列结论:
①,②③,④
其中正确的是( )
A.②④ B.①④ C.②③ D.①③
10. 如图,在平面直角坐标系 中,直线 与坐标轴交于 两点, 于点 是线段 上的一个动点,连接 ,将线段 绕点 逆时针旋转 ,得到线段 ,连接,则线段的最小值为( )
A. B. C.2 D.
二、填空题
11. 如图所示,这个图案绕精它的中心旋转α()后能够与它本身重合,则α可以为 _____(写出一个即可).
12. 如图,中,,将绕A点按顺时针旋转,得到,则______.
13. 如图,是边长为的等边三角形,是的中点,是直线上的一个动点,连接,将线段绕点逆时针旋转得到,连接.则在点的运动过程中,的最小值是______.
14. 如图,正方形,点E在上,点F在上,连接,且,则的长为________.
三、解答题
15. (1)解方程:.
(2)如图,将其绕着某点旋转,能与自身重合,求的最小值.
16. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,的三个顶点,,均在格点上.
(1)画出向左平移4个单位得到的,并写出点的坐标;
(2)画出绕点顺时针旋转后得到的,并写出点的坐标.
17. 如图1,抛物线与x轴交于点,两点,与y轴交于点C,经过点B的直线交y轴于点
(1)求抛物线的解析式
(2)如图2,过点A于作的平行线交抛物线于另一点D,点P是抛物线位于线段下方的一个动点,联结,,,,当四边形面积最大时,求点P坐标.
(3)如图3,连接,将绕点O逆时针旋转,记旋转中的三角形为,在旋转的过程中,直线与直线交于点Q,若为等腰三角形,请直接写出点Q的坐标.
18. 【课本再现】把两个全等的矩形和矩形拼成如图1的图案,则______;
【迁移应用】如图2,在正方形中,E是边上一点(不与点C,D重合),连接,将绕点E顺时针旋转至,作射线交的延长线于点G,求证:;
【拓展延伸】在菱形中,,E是边上一点(不与点C,D
重合),连接,将绕点E顺时针旋转至,作射线交的延长线于点G.
①线段与的数量关系是_______.
②若,E是的三等分点,则的面积为_______.
同课章节目录
