24.1. 3 弧、弦、圆心角 同步练习 (无答案)2023-2024学年人教版数学九年级上册
文档属性
| 名称 | 24.1. 3 弧、弦、圆心角 同步练习 (无答案)2023-2024学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 360.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-11 16:18:29 | ||
图片预览

文档简介
24.1.3 弧、弦、圆心角
一、单选题
1.如图,在中,,则的度数为( )
A. B. C. D.
2.如图,将大小不同的两块量角器的零度线对齐,且小量角器的中心恰好在大量角器的圆周上,设图中两圆周的交点为.且点在小量角器上对应的刻度为,那么点在大量角器上对应的刻度为(只考虑小于的角) ( )
A. B. C. D.
3.如图,计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.若圆的半径为1,当任务完成的百分比为x时,线段MN的长度记为d(x),下列描述正确的是( )
A. B.当时,
C.当时, D.当时,
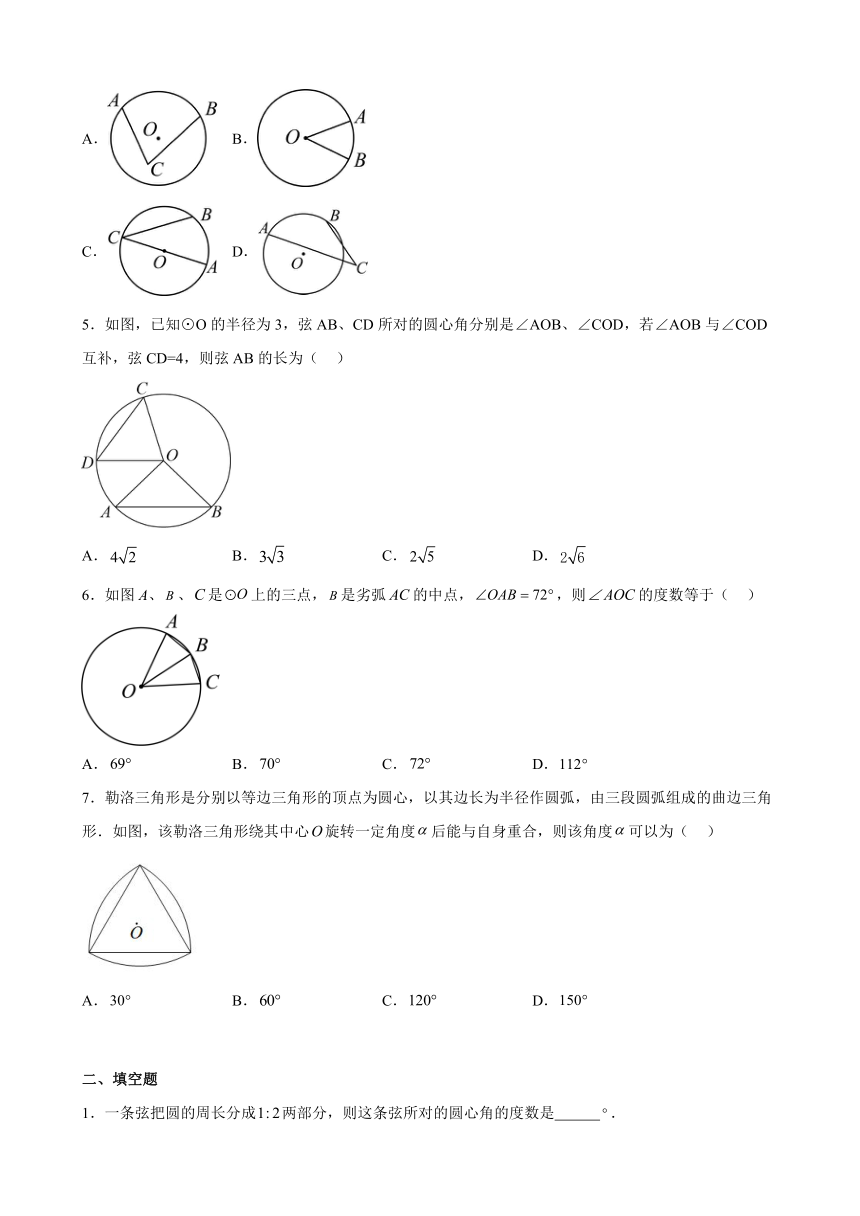
4.下列图形中的角是圆心角的是( )
A. B.
C. D.
5.如图,已知⊙O的半径为3,弦AB、CD所对的圆心角分别是∠AOB、∠COD,若∠AOB与∠COD互补,弦CD=4,则弦AB的长为( )
A. B. C. D.
6.如图A、、是上的三点,是劣弧的中点,,则的度数等于( )
A. B. C. D.
7.勒洛三角形是分别以等边三角形的顶点为圆心,以其边长为半径作圆弧,由三段圆弧组成的曲边三角形.如图,该勒洛三角形绕其中心旋转一定角度后能与自身重合,则该角度可以为( )
A. B. C. D.
二、填空题
1.一条弦把圆的周长分成两部分,则这条弦所对的圆心角的度数是 .
2.为培养学生动手实践能力,学校七年级生物兴趣小组在项目化学习“制作微型生态圈”过程中,设置了一个圆形展厅.如图,在其圆形边缘上的点P处安装了一台监视器,它的监控角度是50°,为了观察到展厅的每个位置,最少需在圆形边缘上共安装这样的监视器 台.
3如图,是△ABC的外接圆,∠BAC=90°,AB=AC,为上一点,连接、OD,延长AC和交于点,若∠E=25°,则∠ODE= .
4.如图,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE= .
5.如图,已知为的直径,为半圆周上的一点,且所对圆心角的度数是所对圆心角度数的2倍,则圆心角 .
三、解答题
1.(1)解方程:.
(2)如图,,,,是上的四个点,且,求证:.
2.如图,在⊙O中,AB是⊙O的弦,CD是⊙O的直径,且AB⊥CD,垂足为G,点E在劣弧上,连接CE.
(1)求证:CE平分∠AEB;
(2)连接BC,若BC//AE,求证:BC=BE.
3.已知:如图,,是的弦,且,,分别是,的中点.求证:
4.如图,在ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E.
(1)若∠A=25°,求的度数;
(2)若BC=9,AC=12,求BD的长.
5.如图1,A,B是上的两点,,C是的中点.
(1)求证:四边形是菱形.
拓展延伸
(2)如图2,将线段绕圆心O逆时针旋转,得到线段,交于点E,连接,若,求的长.
一、单选题
1.如图,在中,,则的度数为( )
A. B. C. D.
2.如图,将大小不同的两块量角器的零度线对齐,且小量角器的中心恰好在大量角器的圆周上,设图中两圆周的交点为.且点在小量角器上对应的刻度为,那么点在大量角器上对应的刻度为(只考虑小于的角) ( )
A. B. C. D.
3.如图,计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.若圆的半径为1,当任务完成的百分比为x时,线段MN的长度记为d(x),下列描述正确的是( )
A. B.当时,
C.当时, D.当时,
4.下列图形中的角是圆心角的是( )
A. B.
C. D.
5.如图,已知⊙O的半径为3,弦AB、CD所对的圆心角分别是∠AOB、∠COD,若∠AOB与∠COD互补,弦CD=4,则弦AB的长为( )
A. B. C. D.
6.如图A、、是上的三点,是劣弧的中点,,则的度数等于( )
A. B. C. D.
7.勒洛三角形是分别以等边三角形的顶点为圆心,以其边长为半径作圆弧,由三段圆弧组成的曲边三角形.如图,该勒洛三角形绕其中心旋转一定角度后能与自身重合,则该角度可以为( )
A. B. C. D.
二、填空题
1.一条弦把圆的周长分成两部分,则这条弦所对的圆心角的度数是 .
2.为培养学生动手实践能力,学校七年级生物兴趣小组在项目化学习“制作微型生态圈”过程中,设置了一个圆形展厅.如图,在其圆形边缘上的点P处安装了一台监视器,它的监控角度是50°,为了观察到展厅的每个位置,最少需在圆形边缘上共安装这样的监视器 台.
3如图,是△ABC的外接圆,∠BAC=90°,AB=AC,为上一点,连接、OD,延长AC和交于点,若∠E=25°,则∠ODE= .
4.如图,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE= .
5.如图,已知为的直径,为半圆周上的一点,且所对圆心角的度数是所对圆心角度数的2倍,则圆心角 .
三、解答题
1.(1)解方程:.
(2)如图,,,,是上的四个点,且,求证:.
2.如图,在⊙O中,AB是⊙O的弦,CD是⊙O的直径,且AB⊥CD,垂足为G,点E在劣弧上,连接CE.
(1)求证:CE平分∠AEB;
(2)连接BC,若BC//AE,求证:BC=BE.
3.已知:如图,,是的弦,且,,分别是,的中点.求证:
4.如图,在ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E.
(1)若∠A=25°,求的度数;
(2)若BC=9,AC=12,求BD的长.
5.如图1,A,B是上的两点,,C是的中点.
(1)求证:四边形是菱形.
拓展延伸
(2)如图2,将线段绕圆心O逆时针旋转,得到线段,交于点E,连接,若,求的长.
同课章节目录
