相似三角形的性质
图片预览


文档简介
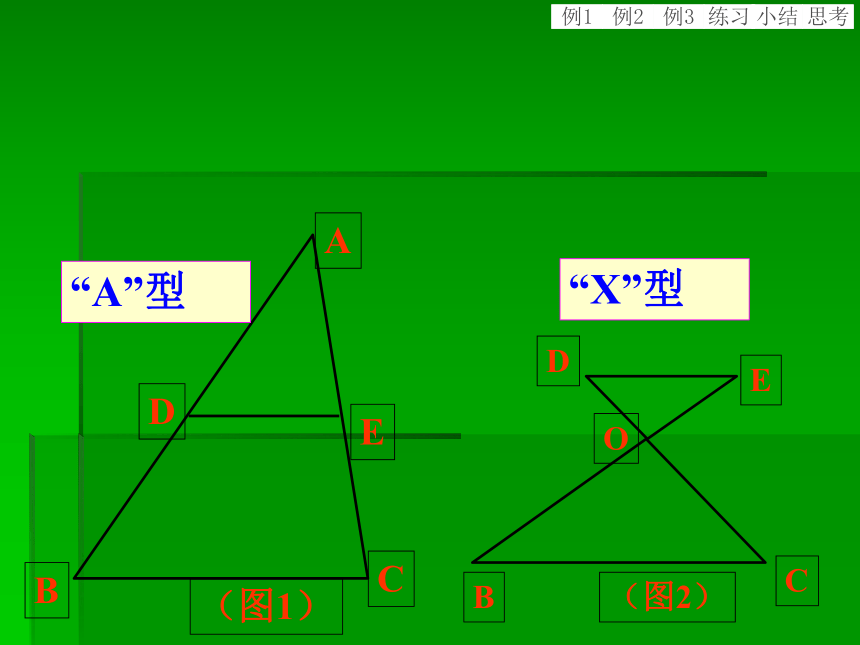
课件15张PPT。“A”型 “X”型 小结例1例2例3练习思考杨汛桥实验学校
柯 丽 萍相似三角形的性质 1.相似三角形对应高的比等于_________,
2.相似三角形对应中线的比等于_______,
3.相似三角形对应角平分线的比等于______。5相似三角形周长的比等于______,
4.相似三角形面积的比等于___________
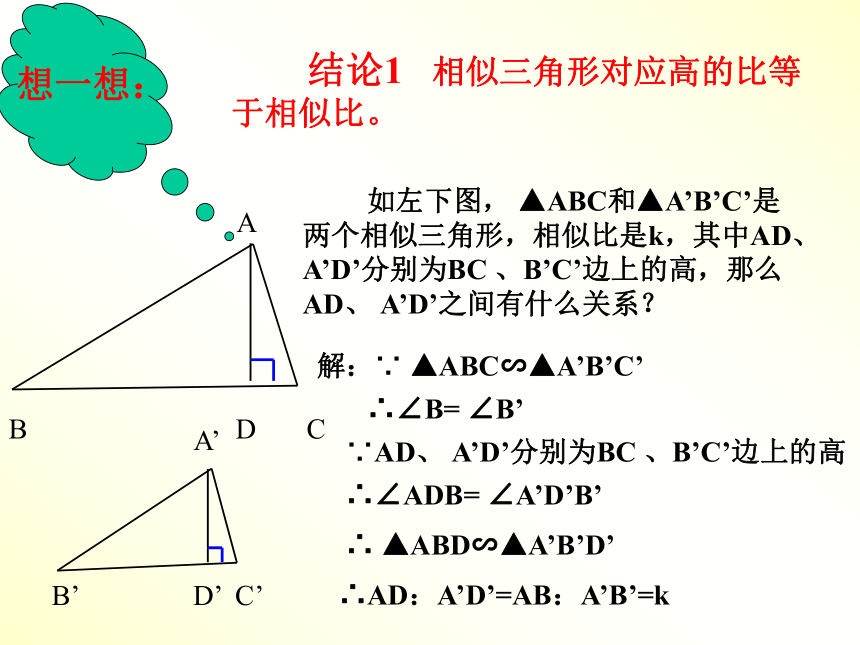
已知两个相似三角形的相似比,求想一想: 如左下图, ▲ABC和▲A’B’C’是两个相似三角形,相似比是k,其中AD、 A’D’分别为BC 、B’C’边上的高,那么AD、 A’D’之间有什么关系?解:∵ ▲ABC∽▲A’B’C’∴∠B= ∠B’∵AD、 A’D’分别为BC 、B’C’边上的高∴∠ADB= ∠A’D’B’ ∴ ▲ABD∽▲A’B’D’∴AD:A’D’=AB:A’B’=k 结论1 相似三角形对应高的比等于相似比。试一试:
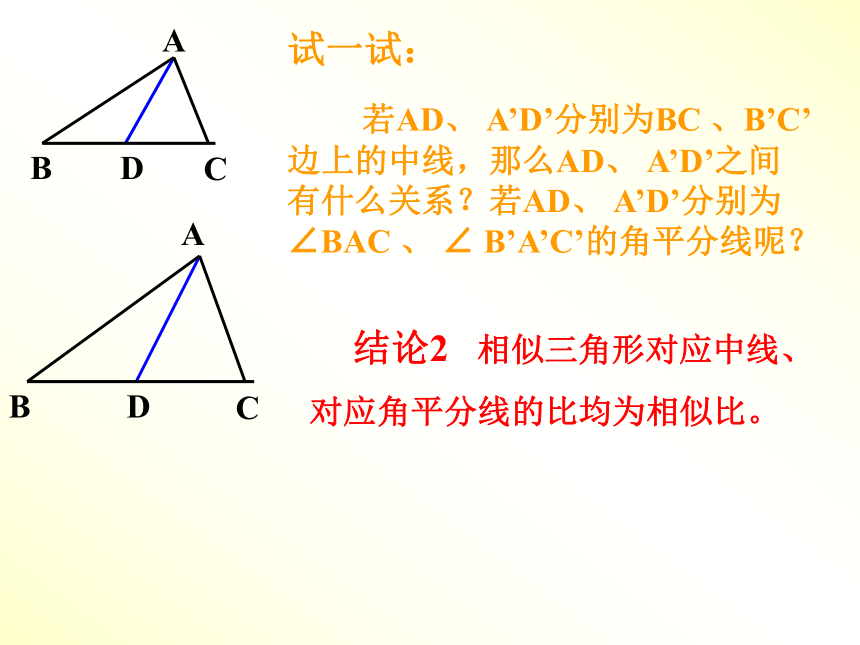
若AD、 A’D’分别为BC 、B’C’边上的中线,那么AD、 A’D’之间有什么关系?若AD、 A’D’分别为∠BAC 、 ∠ B’A’C’的角平分线呢?
结论2 相似三角形对应中线、
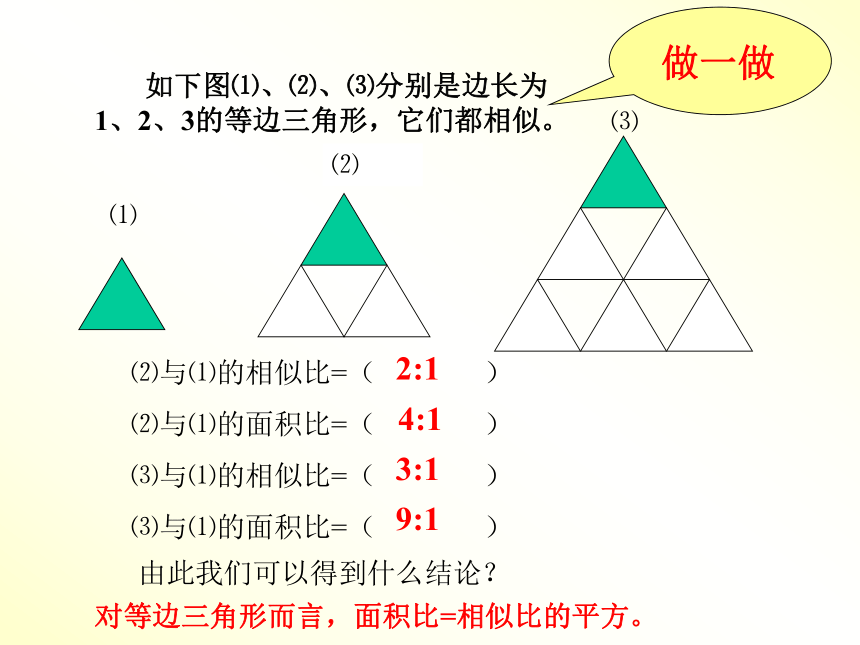
对应角平分线的比均为相似比。做一做 如下图⑴、⑵、⑶分别是边长为1、2、3的等边三角形,它们都相似。⑵与⑴的相似比=( )
⑵与⑴的面积比=( )
⑶与⑴的相似比=( )
⑶与⑴的面积比=( ) 由此我们可以得到什么结论? 对等边三角形而言,面积比=相似比的平方。2:14:13:19:1 动动你聪明的
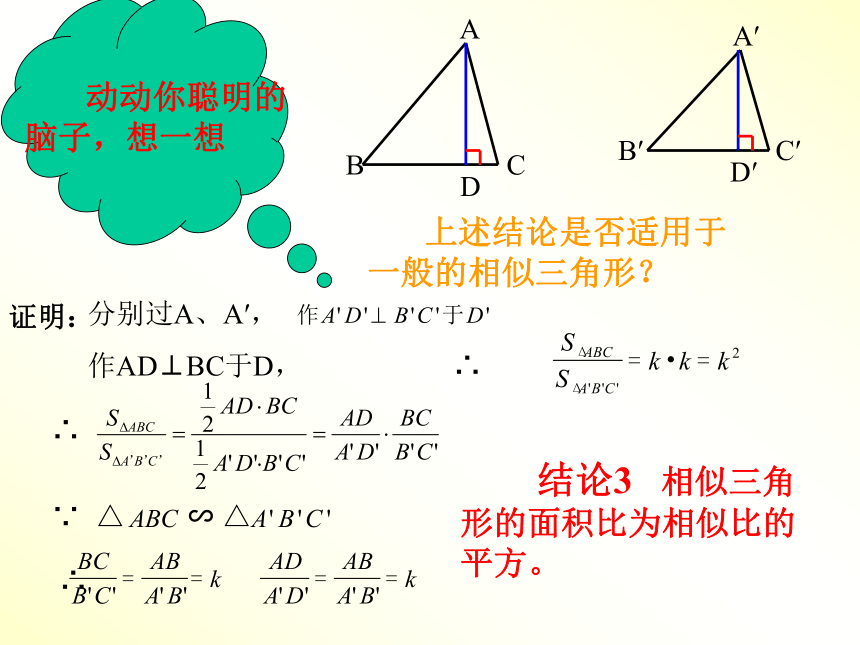
脑子,想一想
上述结论是否适用于一般的相似三角形?DD′证明:分别过A、A′,
作AD⊥BC于D,∵∴∴∴ 结论3 相似三角形的面积比为相似比的平方。相似多边形也有同样的结论吗?想一想(可以以相似四边形为例说明)?两个相似三角形的周长比是多少?结论4 相似三角形的周长比就是相似比。请回答 1、若两个三角形的相似比为3:7,则这两个三角形对应高的比为( ),对应角平分线的比为( ),周长之比为( ),对应中线之比为( )。面积比为( ) 2、把一个三角形改成和它相似的三角形,如果面积扩大为原来的100倍,那么边长扩大为原来的几倍? 3、已知两个等边三角形的边长之比为2:3,且它们的面积之和为26cm2,则较小的等边三角形的面积为多少?3:73:73:710倍8cm23:73.如果边长扩大为原来的5倍,那么面积扩大为
原来的————倍。251、如图,点D、E分别是△ABC边AB、AC上的点,且DE∥BC,BD=2AD,那么
△ADE的周长︰△ABC的周长= 。
△ADE的面积︰△ABC的面积= 。
展示风采:(两边对应成比例,且夹角相等,两三角形相似)∴(相似三角形面积的比等于
相似比的平方)(以下解略)22ACAESSABCADE=DD 1、如图,△ABC中,点D、E、F分别在边AB、AC、BC上,DE∥BC,EF∥AB,AE∕EC=2∕3,S △ABC=S,求S□BFED。当堂训练 如图,在 ABCD中,E是BC上一点,AC与DE相交于F,若AE:EB=1:2,求?AEF与?CDF的相似比。若?AEF的面积为5平方厘米,求?CDF的面积。BFEDCA谢谢
柯 丽 萍相似三角形的性质 1.相似三角形对应高的比等于_________,
2.相似三角形对应中线的比等于_______,
3.相似三角形对应角平分线的比等于______。5相似三角形周长的比等于______,
4.相似三角形面积的比等于___________
已知两个相似三角形的相似比,求想一想: 如左下图, ▲ABC和▲A’B’C’是两个相似三角形,相似比是k,其中AD、 A’D’分别为BC 、B’C’边上的高,那么AD、 A’D’之间有什么关系?解:∵ ▲ABC∽▲A’B’C’∴∠B= ∠B’∵AD、 A’D’分别为BC 、B’C’边上的高∴∠ADB= ∠A’D’B’ ∴ ▲ABD∽▲A’B’D’∴AD:A’D’=AB:A’B’=k 结论1 相似三角形对应高的比等于相似比。试一试:
若AD、 A’D’分别为BC 、B’C’边上的中线,那么AD、 A’D’之间有什么关系?若AD、 A’D’分别为∠BAC 、 ∠ B’A’C’的角平分线呢?
结论2 相似三角形对应中线、
对应角平分线的比均为相似比。做一做 如下图⑴、⑵、⑶分别是边长为1、2、3的等边三角形,它们都相似。⑵与⑴的相似比=( )
⑵与⑴的面积比=( )
⑶与⑴的相似比=( )
⑶与⑴的面积比=( ) 由此我们可以得到什么结论? 对等边三角形而言,面积比=相似比的平方。2:14:13:19:1 动动你聪明的
脑子,想一想
上述结论是否适用于一般的相似三角形?DD′证明:分别过A、A′,
作AD⊥BC于D,∵∴∴∴ 结论3 相似三角形的面积比为相似比的平方。相似多边形也有同样的结论吗?想一想(可以以相似四边形为例说明)?两个相似三角形的周长比是多少?结论4 相似三角形的周长比就是相似比。请回答 1、若两个三角形的相似比为3:7,则这两个三角形对应高的比为( ),对应角平分线的比为( ),周长之比为( ),对应中线之比为( )。面积比为( ) 2、把一个三角形改成和它相似的三角形,如果面积扩大为原来的100倍,那么边长扩大为原来的几倍? 3、已知两个等边三角形的边长之比为2:3,且它们的面积之和为26cm2,则较小的等边三角形的面积为多少?3:73:73:710倍8cm23:73.如果边长扩大为原来的5倍,那么面积扩大为
原来的————倍。251、如图,点D、E分别是△ABC边AB、AC上的点,且DE∥BC,BD=2AD,那么
△ADE的周长︰△ABC的周长= 。
△ADE的面积︰△ABC的面积= 。
展示风采:(两边对应成比例,且夹角相等,两三角形相似)∴(相似三角形面积的比等于
相似比的平方)(以下解略)22ACAESSABCADE=DD 1、如图,△ABC中,点D、E、F分别在边AB、AC、BC上,DE∥BC,EF∥AB,AE∕EC=2∕3,S △ABC=S,求S□BFED。当堂训练 如图,在 ABCD中,E是BC上一点,AC与DE相交于F,若AE:EB=1:2,求?AEF与?CDF的相似比。若?AEF的面积为5平方厘米,求?CDF的面积。BFEDCA谢谢
