23.1 图形的旋转( 第1课时)课件 17张PPT 2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 23.1 图形的旋转( 第1课时)课件 17张PPT 2023-2024学年人教版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-11 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
23.1 图形的旋转
第二十三章 旋转
第1课时
1.掌握旋转的有关概念及基本性质
2.能够根据旋转的基本性质解决实际问题
典型例题
当堂检测
学习目标
课堂总结
概念剖析
上节课我们学移,图中陶罐的运动是平移吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
在日常生活中,除了物体的平行移动外,我们还可以看到许多物体的
旋转现象.
迎风旋转的风车
分秒必争的时钟
运转设备的齿轮
这些图形都有什么共同点呢?
旋转的图形都绕着某个不动的点旋转.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
点O叫做该图形旋转的旋转中心,
我们把一个平面图形绕着平面内某一点O转动一个角度,叫做旋转,
O
图形的旋转由旋转中心、旋转的角度和旋转的方向所决定.
旋转的
角度
顺时针(旋转的方向)
旋转中心在旋转过程中保持不动.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
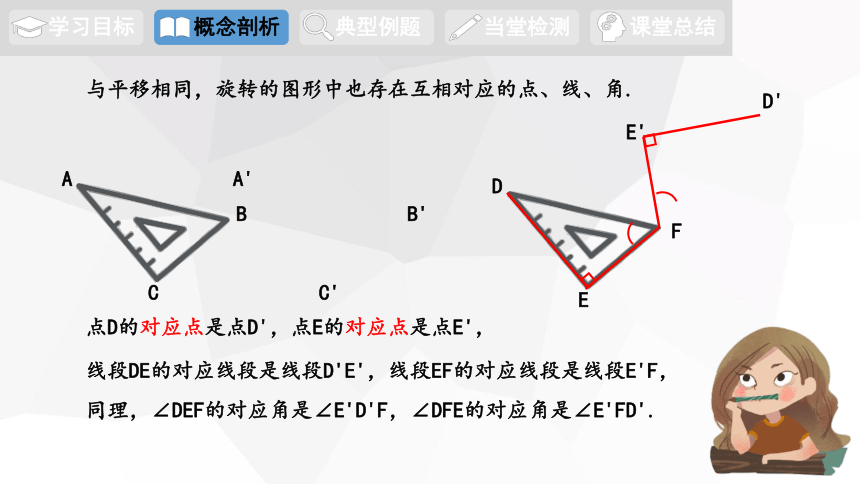
点D的对应点是点D',点E的对应点是点E',
与平移相同,旋转的图形中也存在互相对应的点、线、角.
同理,∠DEF的对应角是∠E'D'F,∠DFE的对应角是∠E'FD'.
线段DE的对应线段是线段D'E',线段EF的对应线段是线段E'F,
A
B
C
D
E
A'
B'
C'
D'
E'
F
典型例题
当堂检测
学习目标
课堂总结
概念剖析
如图,△AOB绕点O旋转得到△ A'OB',你还能发现哪些线段相等?哪些角相等呢?
OA=OA', OB=OB', AB=A'B'
∠AOA'=∠BOB′
∠OA'B'=∠OAB,∠A'B'O=∠ABO,∠A'OB'=∠AOB
联想平移的特征你能概括出旋转的性质吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
图形旋转的性质:
图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度,
对应点与旋转中心所连线段的夹角等于旋转角,
对应点到旋转中心的距离相等,
旋转前、后的图形全等.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.如图,△ABD是等腰直角三角形,C是BD上一点,△ABC经过旋转后到达△ADE的位置.
A
B
C
D
E
P
.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果P是BC的中点,那么经过上述旋转后,点P转到了什么位置?
分析:找到相应的对应点后就能找到旋转后对应的位置,
旋转中保持不动的点是旋转中心,
对应点与旋转中心连线间夹角度数为旋转角度.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.如图,△ABD是等腰直角三角形,C是BD上一点,△ABC经过旋转后到达△ADE的位置.
A
B
C
D
E
P
.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果P是BC的中点,那么经过上述旋转后,点P转到了什么位置?
解:(1)旋转中心是点A;
(2)旋转了90°;
(3)点转到AE中点的位置.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.下列运动属于旋转的是( )
A. 滚动过程中的篮球 B. 一个图形沿某直线对折过程
C. 气球升空的运动 D. 钟表钟摆的摆动
解析:滚动过程中的篮球属于滚动,不是绕着某一个固定的点转动,不属于旋转.
D
典型例题
当堂检测
学习目标
课堂总结
概念剖析
A
O
B
C
D
E
F
解:(1)旋转中心是点O;
(2)点A移动到点D,点B移动到点E的位置;
(3)旋转了120°.
2.如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF.在这个旋转过程中:
(1)旋转中心是什么
(2)经过旋转,点A、B分别移动
到什么位置?
(3)时针从10旋转到2的旋转角度
是多少?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.如图,△ABC和△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,那么哪一点是旋转中心?旋转了多少度?
解:旋转中心是点A,
旋转了45°
A
C
B
D
E
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.已知直角△ABC中, ∠ACB=90°, ∠A=35°,以直角顶点C为旋转中心, 将△ABC旋转到△DEC的位置,斜边DE恰好过点B,直角边CD交AB于O, 求∠BOC的度数.
A
C
B
D
E
O
35°
解:∵BC与EC是对应边,∠E与∠CBA是对应角
∴BC=EC,∠E=∠CBA=∠EBC
∵∠ACB=90°, ∠A=35°
∴∠E=∠CBA=∠EBC=55°
∴∠BC0=20°
∴∠ECB=70°,
∴∠B0C=180°-20°-55°=105°
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.如图,把△ABC绕点A顺时针旋转46 得△ADE,点E恰好在BC边上,则∠C=______度.
67
E
A
B
C
D
典型例题
当堂检测
学习目标
课堂总结
概念剖析
5.如图所示, △ABC是直角三角形, BC是斜边, △ABP绕点A逆时针旋转后,能与△ACP′重合,试判断△APP′的形状.
解:∵△ABC是直角三角形, BC是斜边,
∴△ACP′的旋转角度是90°,
P′
C
B
A
P
又∵AP与AP'是对应线段
∴AP=AP',
∴△APP′是等腰直角三角形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.把一个平面图形绕着平面内某一点O转动一个角度,叫做旋转.
3.决定旋转的因素:
旋转中心、旋转的方向、旋转的角度.
2.围绕的定点O叫做该图形旋转的旋转中心.
4.图形旋转的性质:
对应点与旋转中心所连线段的夹角等于旋转角,
对应点到旋转中心的距离相等,
旋转前、后的图形全等.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
23.1 图形的旋转
第二十三章 旋转
第1课时
1.掌握旋转的有关概念及基本性质
2.能够根据旋转的基本性质解决实际问题
典型例题
当堂检测
学习目标
课堂总结
概念剖析
上节课我们学移,图中陶罐的运动是平移吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
在日常生活中,除了物体的平行移动外,我们还可以看到许多物体的
旋转现象.
迎风旋转的风车
分秒必争的时钟
运转设备的齿轮
这些图形都有什么共同点呢?
旋转的图形都绕着某个不动的点旋转.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
点O叫做该图形旋转的旋转中心,
我们把一个平面图形绕着平面内某一点O转动一个角度,叫做旋转,
O
图形的旋转由旋转中心、旋转的角度和旋转的方向所决定.
旋转的
角度
顺时针(旋转的方向)
旋转中心在旋转过程中保持不动.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
点D的对应点是点D',点E的对应点是点E',
与平移相同,旋转的图形中也存在互相对应的点、线、角.
同理,∠DEF的对应角是∠E'D'F,∠DFE的对应角是∠E'FD'.
线段DE的对应线段是线段D'E',线段EF的对应线段是线段E'F,
A
B
C
D
E
A'
B'
C'
D'
E'
F
典型例题
当堂检测
学习目标
课堂总结
概念剖析
如图,△AOB绕点O旋转得到△ A'OB',你还能发现哪些线段相等?哪些角相等呢?
OA=OA', OB=OB', AB=A'B'
∠AOA'=∠BOB′
∠OA'B'=∠OAB,∠A'B'O=∠ABO,∠A'OB'=∠AOB
联想平移的特征你能概括出旋转的性质吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
图形旋转的性质:
图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度,
对应点与旋转中心所连线段的夹角等于旋转角,
对应点到旋转中心的距离相等,
旋转前、后的图形全等.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.如图,△ABD是等腰直角三角形,C是BD上一点,△ABC经过旋转后到达△ADE的位置.
A
B
C
D
E
P
.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果P是BC的中点,那么经过上述旋转后,点P转到了什么位置?
分析:找到相应的对应点后就能找到旋转后对应的位置,
旋转中保持不动的点是旋转中心,
对应点与旋转中心连线间夹角度数为旋转角度.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.如图,△ABD是等腰直角三角形,C是BD上一点,△ABC经过旋转后到达△ADE的位置.
A
B
C
D
E
P
.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果P是BC的中点,那么经过上述旋转后,点P转到了什么位置?
解:(1)旋转中心是点A;
(2)旋转了90°;
(3)点转到AE中点的位置.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.下列运动属于旋转的是( )
A. 滚动过程中的篮球 B. 一个图形沿某直线对折过程
C. 气球升空的运动 D. 钟表钟摆的摆动
解析:滚动过程中的篮球属于滚动,不是绕着某一个固定的点转动,不属于旋转.
D
典型例题
当堂检测
学习目标
课堂总结
概念剖析
A
O
B
C
D
E
F
解:(1)旋转中心是点O;
(2)点A移动到点D,点B移动到点E的位置;
(3)旋转了120°.
2.如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF.在这个旋转过程中:
(1)旋转中心是什么
(2)经过旋转,点A、B分别移动
到什么位置?
(3)时针从10旋转到2的旋转角度
是多少?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.如图,△ABC和△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,那么哪一点是旋转中心?旋转了多少度?
解:旋转中心是点A,
旋转了45°
A
C
B
D
E
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.已知直角△ABC中, ∠ACB=90°, ∠A=35°,以直角顶点C为旋转中心, 将△ABC旋转到△DEC的位置,斜边DE恰好过点B,直角边CD交AB于O, 求∠BOC的度数.
A
C
B
D
E
O
35°
解:∵BC与EC是对应边,∠E与∠CBA是对应角
∴BC=EC,∠E=∠CBA=∠EBC
∵∠ACB=90°, ∠A=35°
∴∠E=∠CBA=∠EBC=55°
∴∠BC0=20°
∴∠ECB=70°,
∴∠B0C=180°-20°-55°=105°
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.如图,把△ABC绕点A顺时针旋转46 得△ADE,点E恰好在BC边上,则∠C=______度.
67
E
A
B
C
D
典型例题
当堂检测
学习目标
课堂总结
概念剖析
5.如图所示, △ABC是直角三角形, BC是斜边, △ABP绕点A逆时针旋转后,能与△ACP′重合,试判断△APP′的形状.
解:∵△ABC是直角三角形, BC是斜边,
∴△ACP′的旋转角度是90°,
P′
C
B
A
P
又∵AP与AP'是对应线段
∴AP=AP',
∴△APP′是等腰直角三角形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.把一个平面图形绕着平面内某一点O转动一个角度,叫做旋转.
3.决定旋转的因素:
旋转中心、旋转的方向、旋转的角度.
2.围绕的定点O叫做该图形旋转的旋转中心.
4.图形旋转的性质:
对应点与旋转中心所连线段的夹角等于旋转角,
对应点到旋转中心的距离相等,
旋转前、后的图形全等.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
同课章节目录
