2.4 整式分层练习(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
2.4整式
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列式子:,m,,,0,中,整式的个数有( )
A.6 B.5 C.4 D.3
2.观察下列等式:,,,……,用你所发现的规律确定的结果的个位数字为( )
A.2 B. C.6 D.
3.下列说法中,正确的是( )
A.单项式的系数是,次数是3 B.单项式a的系数是0次数是0
C.常数项是1 D.单项式的次数是2,系数为
4.代数式0,,,,,中,单项式有( )
A.2个 B.3个 C.4个 D.5个
5.按照图中图形变化的规律,则第2021个图形中黑色正方形的数量是( )
A.3031 B.3032 C.3033 D.3034
6.以下说法正确的是( )
A.不是正数的数一定是负数 B.oC表示没有温度
C.小华的体重增长了表示小华的体重减少 D.多项式的次数是
7.观察下列数对:(1,1) , (1,2) , (2,1) , (1,3) , (2,2) , (3,1) , (1,4) , (2,3) , (3,2) , (4,1) , (1,5) , (2,4) ,……,那么第32个数对是( )
A.(4, 4) B.(4, 5) C.(4, 6) D.(5, 4)
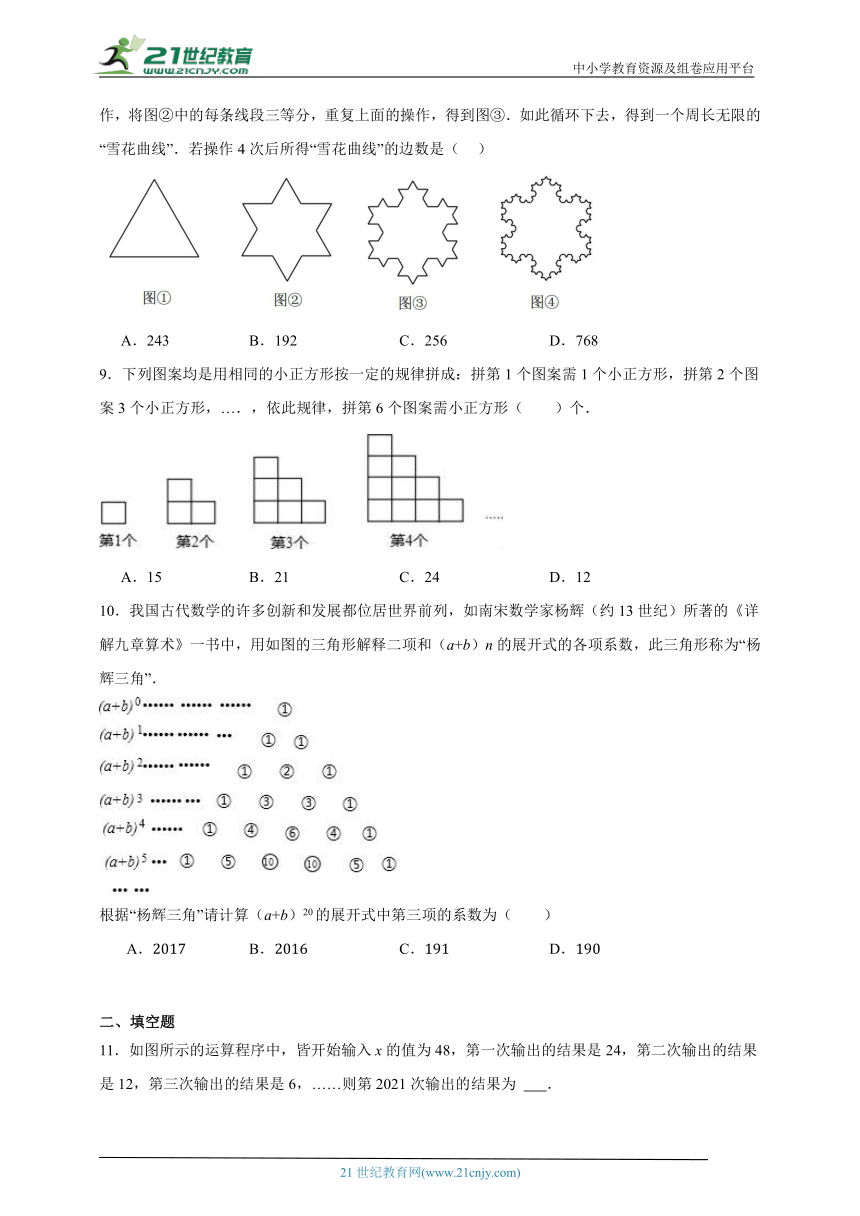
8.“雪花曲线”是瑞典数学家科赫构造的图案(又名科赫曲线).其过程是:第一次操作,将一个等边三角形每边三等分,再以中间一段为边向外作等边三角形,然后去掉中间一段得到图②.第二次操作,将图②中的每条线段三等分,重复上面的操作,得到图③.如此循环下去,得到一个周长无限的“雪花曲线”.若操作4次后所得“雪花曲线”的边数是( )
A.243 B.192 C.256 D.768
9.下列图案均是用相同的小正方形按一定的规律拼成:拼第1个图案需1个小正方形,拼第2个图案3个小正方形,….,依此规律,拼第6个图案需小正方形( )个.
A.15 B.21 C.24 D.12
10.我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.
根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为( )
A.2017 B.2016 C.191 D.190
二、填空题
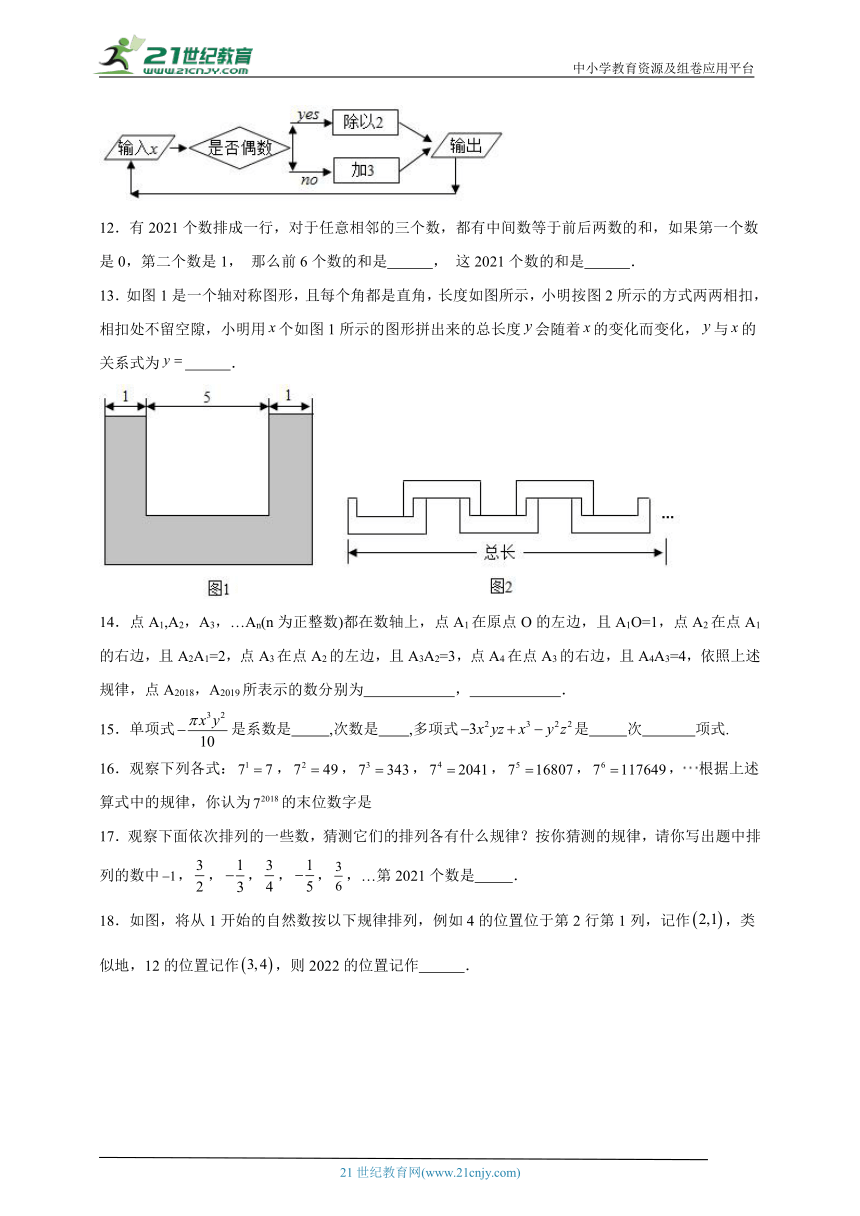
11.如图所示的运算程序中,皆开始输入x的值为48,第一次输出的结果是24,第二次输出的结果是12,第三次输出的结果是6,……则第2021次输出的结果为 .
12.有2021个数排成一行,对于任意相邻的三个数,都有中间数等于前后两数的和,如果第一个数是0,第二个数是1, 那么前6个数的和是 , 这2021个数的和是 .
13.如图1是一个轴对称图形,且每个角都是直角,长度如图所示,小明按图2所示的方式两两相扣,相扣处不留空隙,小明用个如图1所示的图形拼出来的总长度会随着的变化而变化,与的关系式为 .
14.点A1,A2,A3,…An(n为正整数)都在数轴上,点A1在原点O的左边,且A1O=1,点A2在点A1的右边,且A2A1=2,点A3在点A2的左边,且A3A2=3,点A4在点A3的右边,且A4A3=4,依照上述规律,点A2018,A2019所表示的数分别为 , .
15.单项式是系数是 ,次数是 ,多项式是 次 项式.
16.观察下列各式:,,,,,,根据上述算式中的规律,你认为的末位数字是
17.观察下面依次排列的一些数,猜测它们的排列各有什么规律?按你猜测的规律,请你写出题中排列的数中,,,,,,…第2021个数是 .
18.如图,将从1开始的自然数按以下规律排列,例如4的位置位于第2行第1列,记作,类似地,12的位置记作,则2022的位置记作 .
19.下列代数式中,符合代数式书写要求的有 .
(1); (2); (3); (4); (5); (6).
20.已知:,则整式的值为 .
三、解答题
21.(1)关于,的多项式是七次四项式,求和的值;
(2)关于,的多项式不含三次项,求的值.
22.如图,在边长都为a的正方形内分别排列着一些大小相等的圆:
(1)根据图中的规律,第4个正方形内圆的个数是_________,第n个正方形内圆的个数是_________;
(2)如果把正方形内除去圆的部分都涂上阴影;
①用含a的代数式分别表示第1个正方形中、第3个正方形中阴影部分的面积(结果保留);
②若,请直接写出第2021个正方形中阴形都分的面积_________(结果保留.)
23.观察下列式子:将以上三个式子的两边分别相加,得=1
(1)猜想并写出:= .
(2)直接写出:= .
24.探究2:
13+23=______;
13+23+33=______;
13+23+33+43=______;
13+23+33+43+53=______;
13+23+33+43+53+63=______;
13+23+33+43+53+63+73=______;
13+23+33+43+53+63+73+83=______;
13+23+33+43+53+63+73+83+93=______;
13+23+33+43+53+63+73+83+93+103=______;
规律:
25.观察下列等式:
;
;
…
(1)根据上述各式反映的规律填空,使下列式子满足以上规律:
①___;
②____2—____2;
(2)设这类等式左边第一个两位数的十位数字为a,个位数字为b,a、b均为大于0而小于等于9的整数,且,请用a、b写出表示一般规律的式子,并证明所得式子.
参考答案:
1.A
2.D
3.D
4.B
5.B
6.C
7.B
8.D
9.B
10.D
11.6
12. 0 1
13.
14. 1009 -1010
15. 四 三
16.9
17.
18.(45,4)
19.(2)(5).
20.或 /-7或-3
21.(1),;(2)
22.(1)16;;(2)①第一个,第三个;②
23.(1);(2)
24.9,36,100,225,441,784,1296,2025,3025,规律:13+23+33+…+n3=(1+2+3+…+n)2
25.(1)①(62﹣32),②83,38;(2)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.4整式
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列式子:,m,,,0,中,整式的个数有( )
A.6 B.5 C.4 D.3
2.观察下列等式:,,,……,用你所发现的规律确定的结果的个位数字为( )
A.2 B. C.6 D.
3.下列说法中,正确的是( )
A.单项式的系数是,次数是3 B.单项式a的系数是0次数是0
C.常数项是1 D.单项式的次数是2,系数为
4.代数式0,,,,,中,单项式有( )
A.2个 B.3个 C.4个 D.5个
5.按照图中图形变化的规律,则第2021个图形中黑色正方形的数量是( )
A.3031 B.3032 C.3033 D.3034
6.以下说法正确的是( )
A.不是正数的数一定是负数 B.oC表示没有温度
C.小华的体重增长了表示小华的体重减少 D.多项式的次数是
7.观察下列数对:(1,1) , (1,2) , (2,1) , (1,3) , (2,2) , (3,1) , (1,4) , (2,3) , (3,2) , (4,1) , (1,5) , (2,4) ,……,那么第32个数对是( )
A.(4, 4) B.(4, 5) C.(4, 6) D.(5, 4)
8.“雪花曲线”是瑞典数学家科赫构造的图案(又名科赫曲线).其过程是:第一次操作,将一个等边三角形每边三等分,再以中间一段为边向外作等边三角形,然后去掉中间一段得到图②.第二次操作,将图②中的每条线段三等分,重复上面的操作,得到图③.如此循环下去,得到一个周长无限的“雪花曲线”.若操作4次后所得“雪花曲线”的边数是( )
A.243 B.192 C.256 D.768
9.下列图案均是用相同的小正方形按一定的规律拼成:拼第1个图案需1个小正方形,拼第2个图案3个小正方形,….,依此规律,拼第6个图案需小正方形( )个.
A.15 B.21 C.24 D.12
10.我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.
根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为( )
A.2017 B.2016 C.191 D.190
二、填空题
11.如图所示的运算程序中,皆开始输入x的值为48,第一次输出的结果是24,第二次输出的结果是12,第三次输出的结果是6,……则第2021次输出的结果为 .
12.有2021个数排成一行,对于任意相邻的三个数,都有中间数等于前后两数的和,如果第一个数是0,第二个数是1, 那么前6个数的和是 , 这2021个数的和是 .
13.如图1是一个轴对称图形,且每个角都是直角,长度如图所示,小明按图2所示的方式两两相扣,相扣处不留空隙,小明用个如图1所示的图形拼出来的总长度会随着的变化而变化,与的关系式为 .
14.点A1,A2,A3,…An(n为正整数)都在数轴上,点A1在原点O的左边,且A1O=1,点A2在点A1的右边,且A2A1=2,点A3在点A2的左边,且A3A2=3,点A4在点A3的右边,且A4A3=4,依照上述规律,点A2018,A2019所表示的数分别为 , .
15.单项式是系数是 ,次数是 ,多项式是 次 项式.
16.观察下列各式:,,,,,,根据上述算式中的规律,你认为的末位数字是
17.观察下面依次排列的一些数,猜测它们的排列各有什么规律?按你猜测的规律,请你写出题中排列的数中,,,,,,…第2021个数是 .
18.如图,将从1开始的自然数按以下规律排列,例如4的位置位于第2行第1列,记作,类似地,12的位置记作,则2022的位置记作 .
19.下列代数式中,符合代数式书写要求的有 .
(1); (2); (3); (4); (5); (6).
20.已知:,则整式的值为 .
三、解答题
21.(1)关于,的多项式是七次四项式,求和的值;
(2)关于,的多项式不含三次项,求的值.
22.如图,在边长都为a的正方形内分别排列着一些大小相等的圆:
(1)根据图中的规律,第4个正方形内圆的个数是_________,第n个正方形内圆的个数是_________;
(2)如果把正方形内除去圆的部分都涂上阴影;
①用含a的代数式分别表示第1个正方形中、第3个正方形中阴影部分的面积(结果保留);
②若,请直接写出第2021个正方形中阴形都分的面积_________(结果保留.)
23.观察下列式子:将以上三个式子的两边分别相加,得=1
(1)猜想并写出:= .
(2)直接写出:= .
24.探究2:
13+23=______;
13+23+33=______;
13+23+33+43=______;
13+23+33+43+53=______;
13+23+33+43+53+63=______;
13+23+33+43+53+63+73=______;
13+23+33+43+53+63+73+83=______;
13+23+33+43+53+63+73+83+93=______;
13+23+33+43+53+63+73+83+93+103=______;
规律:
25.观察下列等式:
;
;
…
(1)根据上述各式反映的规律填空,使下列式子满足以上规律:
①___;
②____2—____2;
(2)设这类等式左边第一个两位数的十位数字为a,个位数字为b,a、b均为大于0而小于等于9的整数,且,请用a、b写出表示一般规律的式子,并证明所得式子.
参考答案:
1.A
2.D
3.D
4.B
5.B
6.C
7.B
8.D
9.B
10.D
11.6
12. 0 1
13.
14. 1009 -1010
15. 四 三
16.9
17.
18.(45,4)
19.(2)(5).
20.或 /-7或-3
21.(1),;(2)
22.(1)16;;(2)①第一个,第三个;②
23.(1);(2)
24.9,36,100,225,441,784,1296,2025,3025,规律:13+23+33+…+n3=(1+2+3+…+n)2
25.(1)①(62﹣32),②83,38;(2)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
