四川省大竹县文星中学2014-2015学年高一4月月考数学试题
文档属性
| 名称 | 四川省大竹县文星中学2014-2015学年高一4月月考数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 62.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-05 17:38:47 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
四川省大竹县文星中学2015年春高一下期4月月考
数学试卷
时间:120分钟;满分:150分
第I卷(选择题)
一、单项选择:共12题 每题5分 共60分
1.已知A={1,2,3},B={2,4},定义集合A,B间的运算A*B={x|x∈A,且x B},则集合A*B等于( )21教育网
A.{1,2,3} B.{2,3}
C.{1,3} D.{2}
2.已知函数f(x)=,若f(x)=3,则x的值为( )
A.2 B.2或
C.± D.
3.在长方体ABCD-A1B1C1D1六个面中,与面ABCD垂直的有( )
A.1个 B.2个 C.3个 D.4个
4. 已知函数f(x)=,若f[f(0)]=4a,则实数a等于( )
A. B.
C.2 D.9
5. 4.下列命题中,真命题是( )
A.顶点在底面上的射影到底面各顶点的距离相等的三棱锥是正三棱锥
B.底面是正三角形,各侧面是等腰三角形的三棱锥是正三棱锥
C.底面三角形各边分别与相对的侧棱垂直的三棱锥是正三棱锥
D.底面是正三角形,并且侧棱都相等的三棱锥是正三棱锥
6. 两平行平面截半径为5的球,若截面面积分别为9π和16π,则这两个平面间的距离是( )
A.1 B.7
C.3或4 D.1或7
7. 水平放置的矩形ABCD长AB=4, ( http: / / www.21cnjy.com )宽BC=2,以AB、AD为轴作出斜二测直观图A′B′C′D′,则四边形A′B′C′D′的面积为 ( )21cnjy.com
A.4 B.2 C.4 D.2
8. 设长方体的长、宽、高分别为a,b,c,若长方体所有棱的长度之和为24,一条对角线的长度为5,体积为2,则++等于( )www.21-cn-jy.com
A. B. C. D.
9. 若直线l1:y+1=k(x+1)和直线l2关于直线y=x+1对称,那么直线l2恒过定点( )
A.(2,0) B.(1,-1)
C.(1,1) D.(-2,0)
10.设m>0,则直线(x+y)+1+m=0与圆x2+y2=m的位置关系为( )
A.相切 B.相交
C.相切或相离 D.相交或相切
11. 函数f(x)=log(-x2+1)的单调递增区间为( )
A.(-∞,0) B.(0,+∞)
C.(-1,0] D.[0,1)
12. 已知圆x2+y2-2x+my=0上任意一点M关于直线x+y=0的对称点N也在圆上,则m的值为( )2·1·c·n·j·y
A.-1 B.1
C.-2 D.2
第II卷(选择题)
二、填空题:共4题 每题5分 共20分
13. 一棱柱有10个顶点,侧棱长相等,且所有侧棱长的和为100,则其侧棱长为________.
14.Rt△ABC所在平面α外一点P到直角顶点的距离为24,到两直角边的距离都是6,那么点P到平面α的距离等于__________.【来源:21·世纪·教育·网】
15. 直线l:4x-3y+12=0与两坐标轴相交于A、B两点,则线段AB的垂直平分线的方程为__________.21·世纪*教育网
16.下列关于长方体的说法中,正确的是________.
①长方体中有3组对面互相平行;
②长方体ABCD-A1B1C1D1中,与AB垂直的只有棱AD、BC和AA1;
③长方体可看成是由一个矩形平移形成的;
④长方体ABCD-A1B1C1D1中,棱AA1、BB1、CC1、DD1平行且相等.
三、解答题
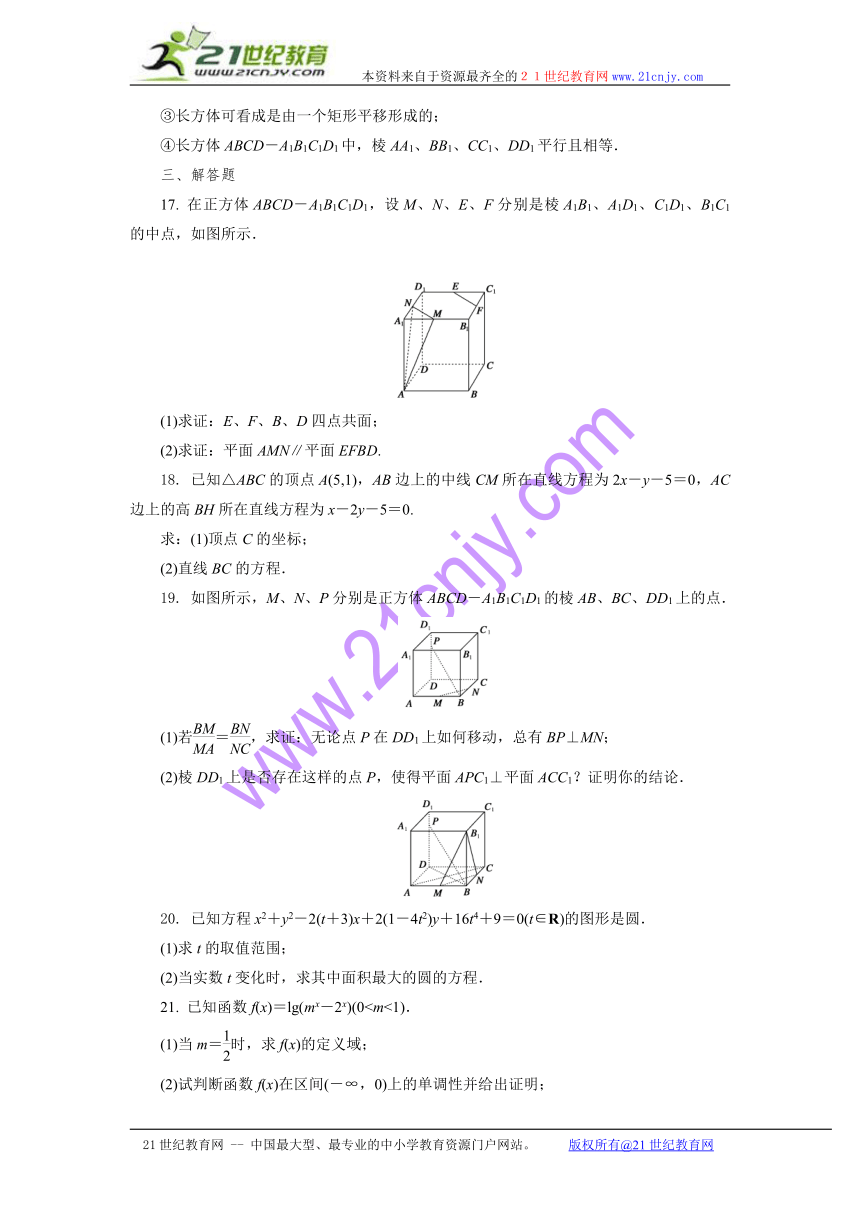
17. 在正方体ABCD-A1B1C1D1,设M、N、E、F分别是棱A1B1、A1D1、C1D1、B1C1的中点,如图所示.www-2-1-cnjy-com
(1)求证:E、F、B、D四点共面;
(2)求证:平面AMN∥平面EFBD.
18. 已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x-y-5=0,AC边上的高BH所在直线方程为x-2y-5=0.2-1-c-n-j-y
求:(1)顶点C的坐标;
(2)直线BC的方程.
19. 如图所示,M、N、P分别是正方体ABCD-A1B1C1D1的棱AB、BC、DD1上的点.
(1)若=,求证:无论点P在DD1上如何移动,总有BP⊥MN;
(2)棱DD1上是否存在这样的点P,使得平面APC1⊥平面ACC1?证明你的结论.
20. 已知方程x2+y2-2(t+3)x+2(1-4t2)y+16t4+9=0(t∈R)的图形是圆.
(1)求t的取值范围;
(2)当实数t变化时,求其中面积最大的圆的方程.
21. 已知函数f(x)=lg(mx-2x)(0(1)当m=时,求f(x)的定义域;
(2)试判断函数f(x)在区间(-∞,0)上的单调性并给出证明;
(3)若f(x)在(-∞,-1]上恒取正值,求m的取值范围.
22.已知⊙C:x2+y2+2x-4y+1=0.
(1)若⊙C的切线在x轴、y轴上截距相等,求切线的方程;
(2)从圆外一点P(x0,y0)向圆引切线PM,M为切点,O为原点,若|PM|=|PO|,求使|PM|最小的P点坐标.21世纪教育网版权所有
1-5.CDDCD 6-10 DBADC 11-12 CD
13. 20
14. 12
15. 6x+8y-7=0
16.①③④
17. (1)分别连接BD、ED、FB,由正方体性质知,B1D1∥BD.
∵E、F分别是C1D1和B1C1的中点,
∴EF綊B1D1,EF綊BD.
∴E、F、B、D四点共面.
(2)连接A1C1交MN于P点,交EF于点Q,分别连接PA、QO.∵M、N分别为A1B1、A1D1的中点,21·cn·jy·com
∴MN∥EF,EF 面EFBD,∴MN∥面EFBD.
∵PQ綊AO,∴四边形PAOQ为平行四边形,
∴PA∥QO.而QO 面EFBD,
∵PA∥面EFBD,且PA∩MN=P,PA、MN 面AMN,
∴平面AMN∥面EFBD.
18.(1)设点C的坐标为(m,n),
∵kBH=,∴kAC=-2,
∴=-2.
又点C(m,n)在直线2x-y-5=0上,
∴2m-n-5=0.
由,得.
∴点C的坐标为(4,3).
(2)设点B的坐标为(a,b),则a-2b-5=0,
AB的中点M的坐标为(,),
∴2--5=0,
即2a-b-1=0.
由,得.
∴点B的坐标为(-1,-3),
∴直线BC的方程为=,
即6x-5y-9=0.
19. (1)如图所示,连接B1M、B1N、AC、BD,则BD⊥AC.
∵=,∴MN∥AC.
∴BD⊥MN.
∵DD1⊥平面ABCD,MN 面ABCD,∴DD1⊥MN.
∴MN⊥平面BDD1.
∵无论P在DD1上如何移动,总有BP 平面BDD1,故总有MN⊥BP.
(2)存在点P,且P为DD1的中点,使得平面APC1⊥平面ACC1.
∵BD⊥AC,BD⊥CC1,
∴BD⊥平面ACC1.
取BD1的中点E,连接PE,
则PE∥BD.∴PE⊥面ACC1.
又∵PE 面APC1,
∴面APC1⊥面ACC1.
20. (1)方程即(x-t-3)2+(y+1-4t2)2
=(t+3)2+(1-4t2)2-16t4-9.
∴r2=-7t2+6t+1>0,∴-(2)∵r==,
∴当t=∈时rmax=,
此时圆面积最大,所对应的圆的方程是
2+2=.
21. (1)当m=时,要使f(x)有意义,须()x-2x>0,即2-x>2x,
可得:-x>x,∴x<0
∴函数f(x)的定义域为{x|x<0}.
(2)设x2<0,x1<0,且x2>x1,则Δ=x2-x1>0
令g(x)=mx-2x,
则g(x2)-g(x1)=mx2-2 x2-m x1+2 x1
=m x2-m x1+2 x1-2 x2
∵0∴m x2-m x1<0,2 x1-2 x2<0
g(x2)-g(x1)<0,∴g(x2)∴lg[g(x2)]∴Δy=lg(g(x2))-lg(g(x1))<0,
∴f(x)在(-∞,0)上是减函数.
(3)由(2)知:f(x)在(-∞,0)上是减函数,
∴f(x)在(-∞,-1]上也为减函数,
∴f(x)在(-∞,-1]上的最小值为f(-1)=lg(m-1-2-1)
所以要使f(x)在(-∞,-1]上恒取正值,
只需f(-1)=lg(m-1-2-1)>0,
即m-1-2-1>1,∴>1+=,
∵022. ⊙C:(x+1)2+(y-2)2=4,
圆心C(-1,2),半径r=2.
(1)若切线过原点设为y=kx,
则=2,∴k=0或.
若切线不过原点,设为x+y=a,
则=2,∴a=1±2,
∴切线方程为:y=0,y=x,
x+y=1+2和x+y=1-2.
(2)=,
∴2x0-4y0+1=0,
|PM|==
∵P在⊙C外,∴(x0+1)2+(y0-2)2>4,
将x0=2y0-代入得5y-2y0+>0,
∴|PM|min=.此时P.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
四川省大竹县文星中学2015年春高一下期4月月考
数学试卷
时间:120分钟;满分:150分
第I卷(选择题)
一、单项选择:共12题 每题5分 共60分
1.已知A={1,2,3},B={2,4},定义集合A,B间的运算A*B={x|x∈A,且x B},则集合A*B等于( )21教育网
A.{1,2,3} B.{2,3}
C.{1,3} D.{2}
2.已知函数f(x)=,若f(x)=3,则x的值为( )
A.2 B.2或
C.± D.
3.在长方体ABCD-A1B1C1D1六个面中,与面ABCD垂直的有( )
A.1个 B.2个 C.3个 D.4个
4. 已知函数f(x)=,若f[f(0)]=4a,则实数a等于( )
A. B.
C.2 D.9
5. 4.下列命题中,真命题是( )
A.顶点在底面上的射影到底面各顶点的距离相等的三棱锥是正三棱锥
B.底面是正三角形,各侧面是等腰三角形的三棱锥是正三棱锥
C.底面三角形各边分别与相对的侧棱垂直的三棱锥是正三棱锥
D.底面是正三角形,并且侧棱都相等的三棱锥是正三棱锥
6. 两平行平面截半径为5的球,若截面面积分别为9π和16π,则这两个平面间的距离是( )
A.1 B.7
C.3或4 D.1或7
7. 水平放置的矩形ABCD长AB=4, ( http: / / www.21cnjy.com )宽BC=2,以AB、AD为轴作出斜二测直观图A′B′C′D′,则四边形A′B′C′D′的面积为 ( )21cnjy.com
A.4 B.2 C.4 D.2
8. 设长方体的长、宽、高分别为a,b,c,若长方体所有棱的长度之和为24,一条对角线的长度为5,体积为2,则++等于( )www.21-cn-jy.com
A. B. C. D.
9. 若直线l1:y+1=k(x+1)和直线l2关于直线y=x+1对称,那么直线l2恒过定点( )
A.(2,0) B.(1,-1)
C.(1,1) D.(-2,0)
10.设m>0,则直线(x+y)+1+m=0与圆x2+y2=m的位置关系为( )
A.相切 B.相交
C.相切或相离 D.相交或相切
11. 函数f(x)=log(-x2+1)的单调递增区间为( )
A.(-∞,0) B.(0,+∞)
C.(-1,0] D.[0,1)
12. 已知圆x2+y2-2x+my=0上任意一点M关于直线x+y=0的对称点N也在圆上,则m的值为( )2·1·c·n·j·y
A.-1 B.1
C.-2 D.2
第II卷(选择题)
二、填空题:共4题 每题5分 共20分
13. 一棱柱有10个顶点,侧棱长相等,且所有侧棱长的和为100,则其侧棱长为________.
14.Rt△ABC所在平面α外一点P到直角顶点的距离为24,到两直角边的距离都是6,那么点P到平面α的距离等于__________.【来源:21·世纪·教育·网】
15. 直线l:4x-3y+12=0与两坐标轴相交于A、B两点,则线段AB的垂直平分线的方程为__________.21·世纪*教育网
16.下列关于长方体的说法中,正确的是________.
①长方体中有3组对面互相平行;
②长方体ABCD-A1B1C1D1中,与AB垂直的只有棱AD、BC和AA1;
③长方体可看成是由一个矩形平移形成的;
④长方体ABCD-A1B1C1D1中,棱AA1、BB1、CC1、DD1平行且相等.
三、解答题
17. 在正方体ABCD-A1B1C1D1,设M、N、E、F分别是棱A1B1、A1D1、C1D1、B1C1的中点,如图所示.www-2-1-cnjy-com
(1)求证:E、F、B、D四点共面;
(2)求证:平面AMN∥平面EFBD.
18. 已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x-y-5=0,AC边上的高BH所在直线方程为x-2y-5=0.2-1-c-n-j-y
求:(1)顶点C的坐标;
(2)直线BC的方程.
19. 如图所示,M、N、P分别是正方体ABCD-A1B1C1D1的棱AB、BC、DD1上的点.
(1)若=,求证:无论点P在DD1上如何移动,总有BP⊥MN;
(2)棱DD1上是否存在这样的点P,使得平面APC1⊥平面ACC1?证明你的结论.
20. 已知方程x2+y2-2(t+3)x+2(1-4t2)y+16t4+9=0(t∈R)的图形是圆.
(1)求t的取值范围;
(2)当实数t变化时,求其中面积最大的圆的方程.
21. 已知函数f(x)=lg(mx-2x)(0
(2)试判断函数f(x)在区间(-∞,0)上的单调性并给出证明;
(3)若f(x)在(-∞,-1]上恒取正值,求m的取值范围.
22.已知⊙C:x2+y2+2x-4y+1=0.
(1)若⊙C的切线在x轴、y轴上截距相等,求切线的方程;
(2)从圆外一点P(x0,y0)向圆引切线PM,M为切点,O为原点,若|PM|=|PO|,求使|PM|最小的P点坐标.21世纪教育网版权所有
1-5.CDDCD 6-10 DBADC 11-12 CD
13. 20
14. 12
15. 6x+8y-7=0
16.①③④
17. (1)分别连接BD、ED、FB,由正方体性质知,B1D1∥BD.
∵E、F分别是C1D1和B1C1的中点,
∴EF綊B1D1,EF綊BD.
∴E、F、B、D四点共面.
(2)连接A1C1交MN于P点,交EF于点Q,分别连接PA、QO.∵M、N分别为A1B1、A1D1的中点,21·cn·jy·com
∴MN∥EF,EF 面EFBD,∴MN∥面EFBD.
∵PQ綊AO,∴四边形PAOQ为平行四边形,
∴PA∥QO.而QO 面EFBD,
∵PA∥面EFBD,且PA∩MN=P,PA、MN 面AMN,
∴平面AMN∥面EFBD.
18.(1)设点C的坐标为(m,n),
∵kBH=,∴kAC=-2,
∴=-2.
又点C(m,n)在直线2x-y-5=0上,
∴2m-n-5=0.
由,得.
∴点C的坐标为(4,3).
(2)设点B的坐标为(a,b),则a-2b-5=0,
AB的中点M的坐标为(,),
∴2--5=0,
即2a-b-1=0.
由,得.
∴点B的坐标为(-1,-3),
∴直线BC的方程为=,
即6x-5y-9=0.
19. (1)如图所示,连接B1M、B1N、AC、BD,则BD⊥AC.
∵=,∴MN∥AC.
∴BD⊥MN.
∵DD1⊥平面ABCD,MN 面ABCD,∴DD1⊥MN.
∴MN⊥平面BDD1.
∵无论P在DD1上如何移动,总有BP 平面BDD1,故总有MN⊥BP.
(2)存在点P,且P为DD1的中点,使得平面APC1⊥平面ACC1.
∵BD⊥AC,BD⊥CC1,
∴BD⊥平面ACC1.
取BD1的中点E,连接PE,
则PE∥BD.∴PE⊥面ACC1.
又∵PE 面APC1,
∴面APC1⊥面ACC1.
20. (1)方程即(x-t-3)2+(y+1-4t2)2
=(t+3)2+(1-4t2)2-16t4-9.
∴r2=-7t2+6t+1>0,∴-
∴当t=∈时rmax=,
此时圆面积最大,所对应的圆的方程是
2+2=.
21. (1)当m=时,要使f(x)有意义,须()x-2x>0,即2-x>2x,
可得:-x>x,∴x<0
∴函数f(x)的定义域为{x|x<0}.
(2)设x2<0,x1<0,且x2>x1,则Δ=x2-x1>0
令g(x)=mx-2x,
则g(x2)-g(x1)=mx2-2 x2-m x1+2 x1
=m x2-m x1+2 x1-2 x2
∵0
g(x2)-g(x1)<0,∴g(x2)
∴f(x)在(-∞,0)上是减函数.
(3)由(2)知:f(x)在(-∞,0)上是减函数,
∴f(x)在(-∞,-1]上也为减函数,
∴f(x)在(-∞,-1]上的最小值为f(-1)=lg(m-1-2-1)
所以要使f(x)在(-∞,-1]上恒取正值,
只需f(-1)=lg(m-1-2-1)>0,
即m-1-2-1>1,∴>1+=,
∵0
圆心C(-1,2),半径r=2.
(1)若切线过原点设为y=kx,
则=2,∴k=0或.
若切线不过原点,设为x+y=a,
则=2,∴a=1±2,
∴切线方程为:y=0,y=x,
x+y=1+2和x+y=1-2.
(2)=,
∴2x0-4y0+1=0,
|PM|==
∵P在⊙C外,∴(x0+1)2+(y0-2)2>4,
将x0=2y0-代入得5y-2y0+>0,
∴|PM|min=.此时P.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
