5.2.2 平行线的判定课件
文档属性
| 名称 | 5.2.2 平行线的判定课件 |  | |
| 格式 | zip | ||
| 文件大小 | 166.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-04 16:32:46 | ||
图片预览



文档简介
课件20张PPT。5.2.2 平行线的判定(2)知识回顾:两条直线平行的判定方法
方法1:如图1,若∠1=∠3,则a∥c
( )
方法2:如图1,若∠2=∠3,则a∥c
( )
方法3:如图1,若∠3+∠4=180°,则a∥c
( )同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行a
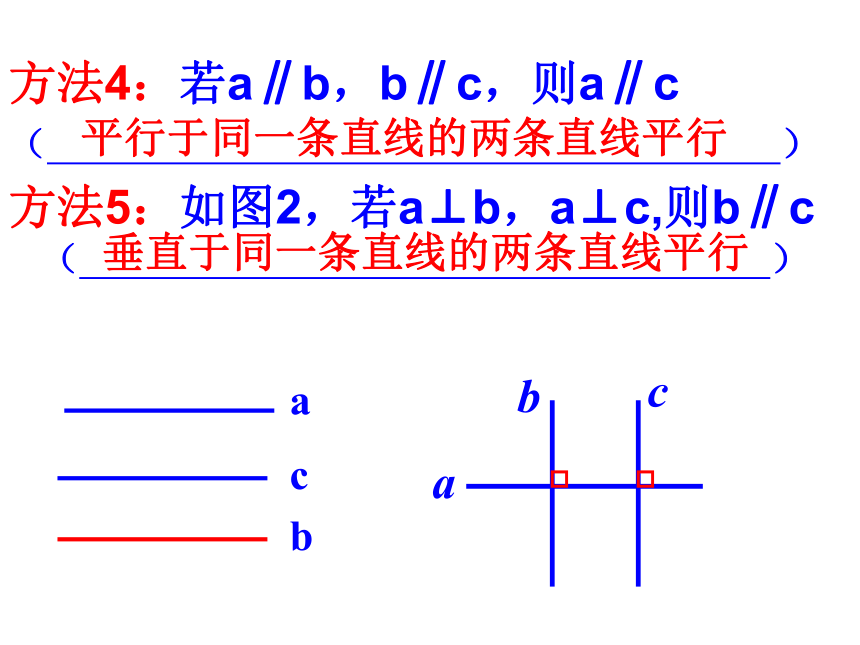
bc)))1234方法4:若a∥b,b∥c,则a∥c
( )
方法5:如图2,若a⊥b,a⊥c,则b∥c( )平行于同一条直线的两条直线平行 垂直于同一条直线的两条直线平行a
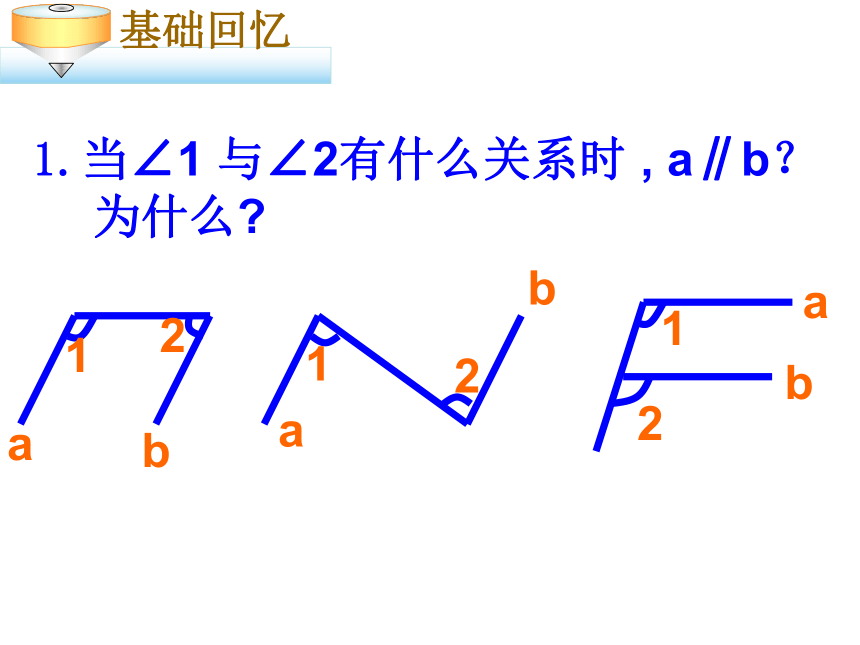
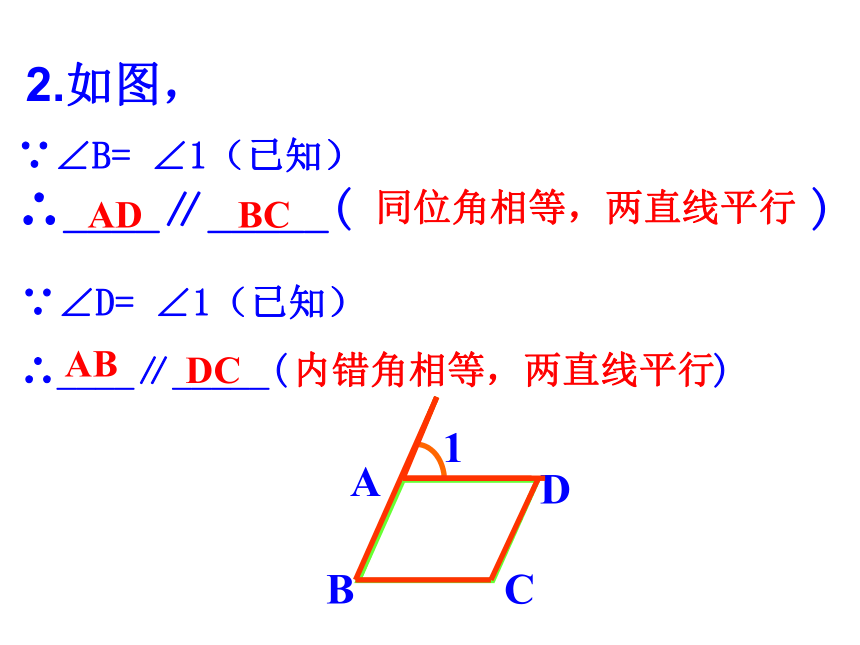
bcabc 1.当∠1 与∠2有什么关系时 , a∥b?为什么? ababba121212∵∠B= ∠1(已知) ∴____∥_____( ) 1ABDC∵∠D= ∠1(已知)
∴____∥_____( ) ADBC同位角相等,两直线平行ABDC内错角相等,两直线平行2.如图,3.如图,
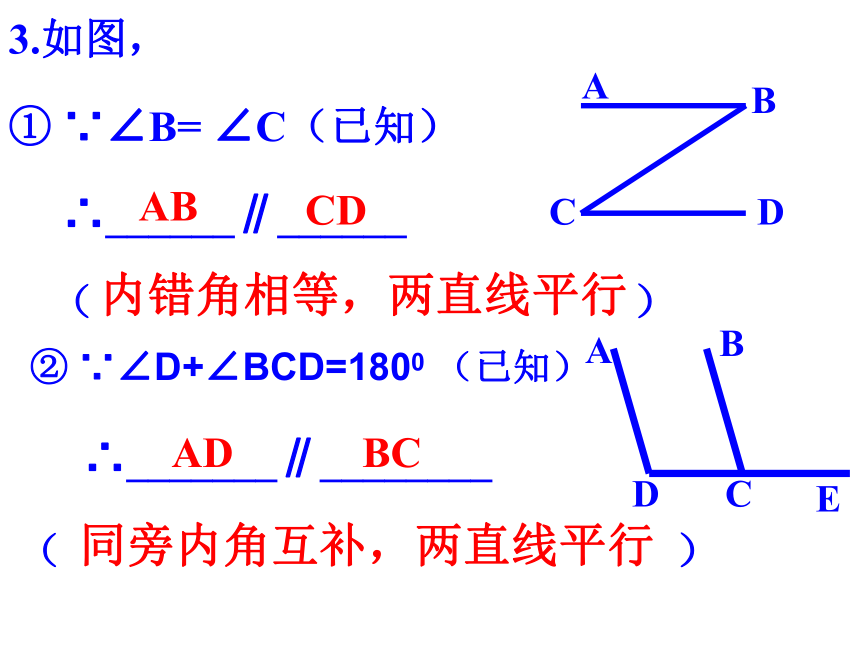
① ∵∠B= ∠C(已知)
∴______∥______
( ) ② ∵∠D+∠BCD=1800 (已知)
∴_______∥________
( )内错角相等,两直线平行EABCDADBC 同旁内角互补,两直线平行(1)∵∠1 =∠4(已知)
∴____∥____( )
(2)∵∠___= ∠___(已知)
∴BC ∥ EF( )
(3) ∵∠1= ∠___(已知)
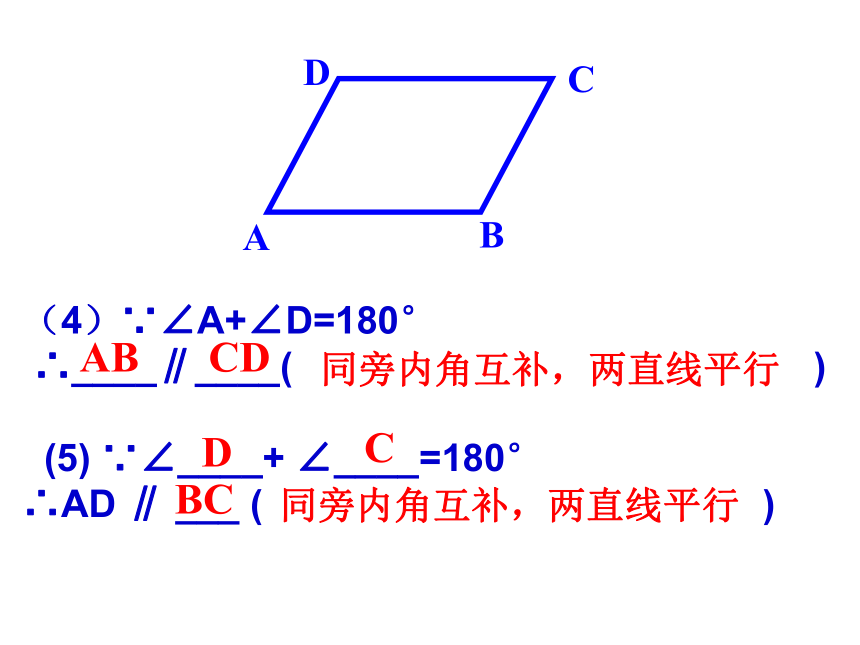
∴DE ∥____( )4、 GCFEBHDA4123GHBC23内错角相等,两直线平行内错角相等,两直线平行2AB内错角相等,两直线平行(4)∵∠A+∠D=180°
∴____∥____( )
(5) ∵∠____+ ∠____=180°
∴AD ∥ ___ ( )ADCBABCD 同旁内角互补,两直线平行DCBC 同旁内角互补,两直线平行ABCDEFGH5、如图:当∠ABH= 时,AB∥DE
当∠ABE + =180°时,AB∥DE
当∠HBC= 时,BC ∥EF
当∠GBC= 时,BC ∥EF课内练习∠DEH∠DEB∠FEH∠GEF (1)如图1,∠C=57°,
当∠ABE= °时,就能使BE∥CD. (2)如图2 , ∠1=120°,∠2=60°.
问a与b的关系? 图1图2a∥b ABECD 5736、57°120°60°能力挑战:(A)∠2=∠3 (B)∠1=∠4
(C)∠1=∠2 (D)∠1=∠3 D7、如图,不能判定 的是 ( )能力挑战:8、如图,∠1=∠2,则下列结论正确的是( )(A)AD//BC (B)AB//CD
(C)AD//EF (D)EF//BCC例1:已知:如图,ABC、CDE都是直线, 且∠1=∠2,∠1=∠C,
求证:AC∥FD.
∵ ∠1 = ∠2,
∠1 = ∠C (已知) ∴ ∠2=∠C (等量代换) ∴ AC∥FD (同位角相等,两直线平行) 21证明:例2: 如图,已知∠1=120°, ∠C=60°
判断直线AB与CD是否平行?)1)2答: AB∥CD理由如下:∵ ∠1=120°( )已知 ∴ ∠2=180°—∠1 =60°
( )
邻补角定义又∵ ∠C=60°( )已知 ∴ ∠2= ∠C( )
等量代换∴AB∥CD( )
同位角相等,两直线平行120°60°还有其它
解法吗?3例3:如图,已知∠1= ∠3,AC平分∠DAB你
能判断那两条直线平行?请说明理由?))1)2(3ABCD答: AB∥CD
理由如下:∵ AC平分∠DAB( )
已知∴ ∠1=∠2( )角平分线定义又∵ ∠1= ∠3( )
已知∴ ∠2=∠3( )等量代换∴ AB∥CD( )
内错角相等,两直线平行练习1:如图,直线EF与∠ABC的一边BA,相交
于D, ∠B+ ∠ADE=180°,EF与BC平行吗?
为什么?答: EF//BC理由如下:∵ ∠B+ ∠1=180( )已知∠1= ∠2( )
对顶角相等∴ ∠B+ ∠2=180°( )等量代换∴ EF∥BC( )
同旁内角互补,两直线平行12还有其它解法吗?3练习2:如图, ∠B=∠C ∠B+∠D=180°,
那么BC平行DE吗?为什么?答:BC∥DE
理由如下:∵ ∠B=∠C ( )已知∠B+ ∠D=180°( )
已知∴ ∠C+ ∠D=180°( )等量代换∴BC∥DE( )同旁内角互补,两直线平行∵ ∠1=∠C (已知) ∴ MN∥BC (内错角相等,两直线平行) ∵ ∠2=∠B (已知) ∴ EF∥BC (同位角相等,两直线平行) ∴ MN∥EF ( ) 证明:FEMNA21BC练习3:已知:如图,∠1=∠C,∠2=∠B,
求证:MN∥EF.
平行于同一直线的两条直线平行判定两条直线是否平行的方法有:1.平行线的定义.2.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
3 .平行线的判定:(1)同位角相等, 两直线平行.
(2)内错角相等, 两直线平行.(3)同旁内角互补, 两直线平行.4.如果两条直线都与第三条直线垂直,
那么这两条直线也互相平行.
归纳小结:归纳小结:作业1、课本P17页 第12 题
数学练习册P20页第4、5题
2、数学练习册P18-21页
方法1:如图1,若∠1=∠3,则a∥c
( )
方法2:如图1,若∠2=∠3,则a∥c
( )
方法3:如图1,若∠3+∠4=180°,则a∥c
( )同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行a
bc)))1234方法4:若a∥b,b∥c,则a∥c
( )
方法5:如图2,若a⊥b,a⊥c,则b∥c( )平行于同一条直线的两条直线平行 垂直于同一条直线的两条直线平行a
bcabc 1.当∠1 与∠2有什么关系时 , a∥b?为什么? ababba121212∵∠B= ∠1(已知) ∴____∥_____( ) 1ABDC∵∠D= ∠1(已知)
∴____∥_____( ) ADBC同位角相等,两直线平行ABDC内错角相等,两直线平行2.如图,3.如图,
① ∵∠B= ∠C(已知)
∴______∥______
( ) ② ∵∠D+∠BCD=1800 (已知)
∴_______∥________
( )内错角相等,两直线平行EABCDADBC 同旁内角互补,两直线平行(1)∵∠1 =∠4(已知)
∴____∥____( )
(2)∵∠___= ∠___(已知)
∴BC ∥ EF( )
(3) ∵∠1= ∠___(已知)
∴DE ∥____( )4、 GCFEBHDA4123GHBC23内错角相等,两直线平行内错角相等,两直线平行2AB内错角相等,两直线平行(4)∵∠A+∠D=180°
∴____∥____( )
(5) ∵∠____+ ∠____=180°
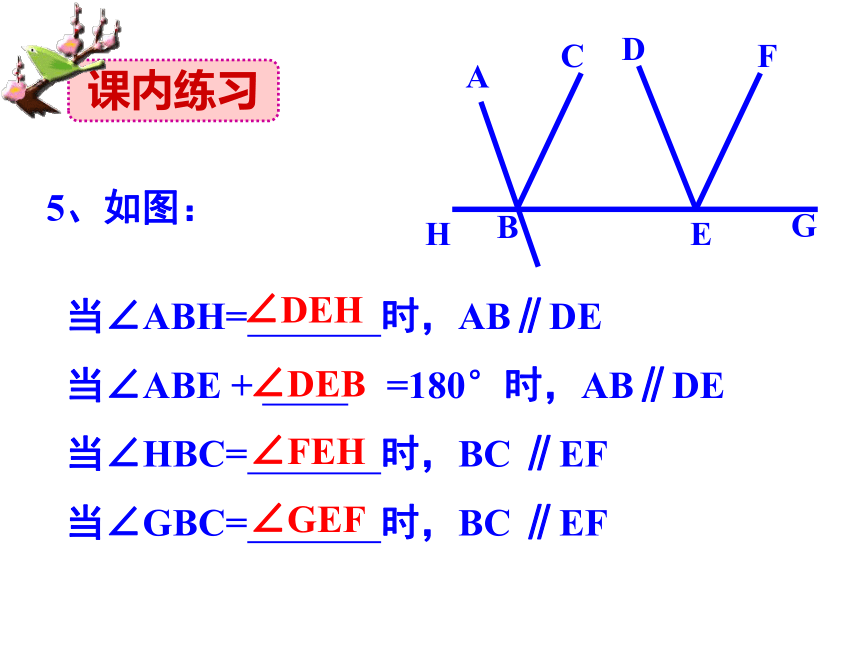
∴AD ∥ ___ ( )ADCBABCD 同旁内角互补,两直线平行DCBC 同旁内角互补,两直线平行ABCDEFGH5、如图:当∠ABH= 时,AB∥DE
当∠ABE + =180°时,AB∥DE
当∠HBC= 时,BC ∥EF
当∠GBC= 时,BC ∥EF课内练习∠DEH∠DEB∠FEH∠GEF (1)如图1,∠C=57°,
当∠ABE= °时,就能使BE∥CD. (2)如图2 , ∠1=120°,∠2=60°.
问a与b的关系? 图1图2a∥b ABECD 5736、57°120°60°能力挑战:(A)∠2=∠3 (B)∠1=∠4
(C)∠1=∠2 (D)∠1=∠3 D7、如图,不能判定 的是 ( )能力挑战:8、如图,∠1=∠2,则下列结论正确的是( )(A)AD//BC (B)AB//CD
(C)AD//EF (D)EF//BCC例1:已知:如图,ABC、CDE都是直线, 且∠1=∠2,∠1=∠C,
求证:AC∥FD.
∵ ∠1 = ∠2,
∠1 = ∠C (已知) ∴ ∠2=∠C (等量代换) ∴ AC∥FD (同位角相等,两直线平行) 21证明:例2: 如图,已知∠1=120°, ∠C=60°
判断直线AB与CD是否平行?)1)2答: AB∥CD理由如下:∵ ∠1=120°( )已知 ∴ ∠2=180°—∠1 =60°
( )
邻补角定义又∵ ∠C=60°( )已知 ∴ ∠2= ∠C( )
等量代换∴AB∥CD( )
同位角相等,两直线平行120°60°还有其它
解法吗?3例3:如图,已知∠1= ∠3,AC平分∠DAB你
能判断那两条直线平行?请说明理由?))1)2(3ABCD答: AB∥CD
理由如下:∵ AC平分∠DAB( )
已知∴ ∠1=∠2( )角平分线定义又∵ ∠1= ∠3( )
已知∴ ∠2=∠3( )等量代换∴ AB∥CD( )
内错角相等,两直线平行练习1:如图,直线EF与∠ABC的一边BA,相交
于D, ∠B+ ∠ADE=180°,EF与BC平行吗?
为什么?答: EF//BC理由如下:∵ ∠B+ ∠1=180( )已知∠1= ∠2( )
对顶角相等∴ ∠B+ ∠2=180°( )等量代换∴ EF∥BC( )
同旁内角互补,两直线平行12还有其它解法吗?3练习2:如图, ∠B=∠C ∠B+∠D=180°,
那么BC平行DE吗?为什么?答:BC∥DE
理由如下:∵ ∠B=∠C ( )已知∠B+ ∠D=180°( )
已知∴ ∠C+ ∠D=180°( )等量代换∴BC∥DE( )同旁内角互补,两直线平行∵ ∠1=∠C (已知) ∴ MN∥BC (内错角相等,两直线平行) ∵ ∠2=∠B (已知) ∴ EF∥BC (同位角相等,两直线平行) ∴ MN∥EF ( ) 证明:FEMNA21BC练习3:已知:如图,∠1=∠C,∠2=∠B,
求证:MN∥EF.
平行于同一直线的两条直线平行判定两条直线是否平行的方法有:1.平行线的定义.2.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
3 .平行线的判定:(1)同位角相等, 两直线平行.
(2)内错角相等, 两直线平行.(3)同旁内角互补, 两直线平行.4.如果两条直线都与第三条直线垂直,
那么这两条直线也互相平行.
归纳小结:归纳小结:作业1、课本P17页 第12 题
数学练习册P20页第4、5题
2、数学练习册P18-21页
