29.3 课题学习 制作立体模型 课件(共17张PPT) 2023-2024学年人教版九年级数学下册
文档属性
| 名称 | 29.3 课题学习 制作立体模型 课件(共17张PPT) 2023-2024学年人教版九年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 375.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-11 22:42:54 | ||
图片预览






文档简介
(共17张PPT)
九年级·数学·人教版·上册
29.3 课题学习 制作立体模型
29.3 课题学习 制作立体模型
1.经历由三视图制作立体模型的实践活动,进一步感受立体图形与平面图形之间的联系与转化.
2.通过“观察、想象、制作、交流”的动手实践活动,增强学生的创新意识与创造发明的意识.
◎重点:根据简单物体的三视图和平面展开图制作立体模型.
◎难点:由物体的三视图或展开图确定物体的形状.
世界闻名的大科学家爱因斯坦读小学的时候,有一次上劳作课,同学们都交上了自己的作品:泥鸭、布娃娃等,唯独爱因斯坦没有交,直到第二天,他才送去一只做得很粗陋的小板凳.老师看了很不满意,说:“我想,世上不会有比这更坏的小板凳了.”爱因斯坦回答说:“有的.”他不慌不忙地从课桌下面拿出两只小板凳,举起左手说:“这是我第一次做的.”又举起右手说:“这是我第二次
做的,刚才交的,是我第三次做的,虽然它还不能使人满意,但总比这两只强一些.” 于是老师改变了对他的态度.今天我们也来动手做立体模型,看谁的手更巧.
制作立体模型
阅读课本本课时的内容,填空:
归纳总结 由三视图或展开图制作立体模型,一般先由三视图或展开图想象出 图形,进而制作出模型.
立体
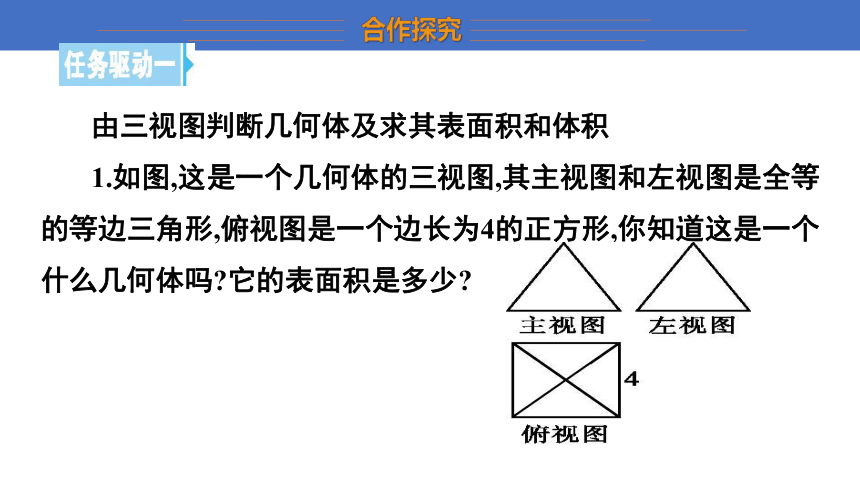
由三视图判断几何体及求其表面积和体积
1.如图,这是一个几何体的三视图,其主视图和左视图是全等的等边三角形,俯视图是一个边长为4的正方形,你知道这是一个什么几何体吗 它的表面积是多少
解:这是一个正四棱锥,如图,它的表面是由四个等腰三角形和一个正方形组成,一个等腰三角形的面积是8,四个等腰三角形的面积是32,所以表面积是48.
变式演练 如图,这是一个几何体的三视图,求这个几何体的表面积和体积.
解:由几何体的三视图可知这个几何体是一个下面是圆柱,上面是圆锥的简单几何体.
圆柱底面直径为4,高为2,圆锥高为3,母线长为=,其表面积为S=πrl+2πrh+πr2=π×2×+8π+4π=2(6+)π(cm2),体积为V=S·h1+S·h2=×π×22×3+π×22×2=12π (cm3).
与立体模型有关的计算
2.拿一张长为a,宽为b的纸,作一圆柱的侧面,用不同的方法作成两种圆柱,画出图形并求这两种圆柱的表面积.(结果保留π)
解:如图,第一种:高为a,表面积为S1=ab+;
第二种:高为b,表面积为S2=ab+.
方法归纳交流 可将a作为圆柱的高,此时底面周长为 ;也可将 作为圆柱的高,此时底面周长为 .
b
b
a
变式演练 图1是一张长为18 cm,宽为12 cm的长方形硬纸板.把它的四个角都剪去一个边长为x cm的小正方形,然后把它折成一个无盖的长方体盒子(如图2),请回答下列问题:
(1)折成的无盖长方体盒子的容积V= cm3.(用含x的代数式表示即可,不需化简)
(2)请完成下表,并根据表格回答,当x取什么正整数时,长方体盒子的容积最大
(3)从正面看折成的长方体盒子,它的形状可能是正方形吗 如果是正方形,求出x的值;如果不是正方形,请说明理由.
x/ cm 1 2 3 4 5
V/ cm3 160 216 80
解:(1)由题意,得长方体盒子的长为(18-2x)、宽为(12-2x)、高为x,因此体积为(18-2x)·(12-2x)·x,
故答案为(18-2x)·(12-2x)·x.
(2)把x=2代入(18-2x)·(12-2x)·x,得(18-2x)·(12-2x)·x=14×8×2=224,
把x=4代入(18-2x)·(12-2x)·x得,(18-2x)·(12-2x)·x=10×4×4=160,
故答案为224,160.
由表可知当x取2时,长方体盒子的容积最大.
(3)它的形状不可能是正方形,理由如下:
当18-2x=x时,即x=6,而当x=6时,图1的短边变为0,因此折不成长方体,故从正面看是正方形是不可能的.
九年级·数学·人教版·上册
29.3 课题学习 制作立体模型
29.3 课题学习 制作立体模型
1.经历由三视图制作立体模型的实践活动,进一步感受立体图形与平面图形之间的联系与转化.
2.通过“观察、想象、制作、交流”的动手实践活动,增强学生的创新意识与创造发明的意识.
◎重点:根据简单物体的三视图和平面展开图制作立体模型.
◎难点:由物体的三视图或展开图确定物体的形状.
世界闻名的大科学家爱因斯坦读小学的时候,有一次上劳作课,同学们都交上了自己的作品:泥鸭、布娃娃等,唯独爱因斯坦没有交,直到第二天,他才送去一只做得很粗陋的小板凳.老师看了很不满意,说:“我想,世上不会有比这更坏的小板凳了.”爱因斯坦回答说:“有的.”他不慌不忙地从课桌下面拿出两只小板凳,举起左手说:“这是我第一次做的.”又举起右手说:“这是我第二次
做的,刚才交的,是我第三次做的,虽然它还不能使人满意,但总比这两只强一些.” 于是老师改变了对他的态度.今天我们也来动手做立体模型,看谁的手更巧.
制作立体模型
阅读课本本课时的内容,填空:
归纳总结 由三视图或展开图制作立体模型,一般先由三视图或展开图想象出 图形,进而制作出模型.
立体
由三视图判断几何体及求其表面积和体积
1.如图,这是一个几何体的三视图,其主视图和左视图是全等的等边三角形,俯视图是一个边长为4的正方形,你知道这是一个什么几何体吗 它的表面积是多少
解:这是一个正四棱锥,如图,它的表面是由四个等腰三角形和一个正方形组成,一个等腰三角形的面积是8,四个等腰三角形的面积是32,所以表面积是48.
变式演练 如图,这是一个几何体的三视图,求这个几何体的表面积和体积.
解:由几何体的三视图可知这个几何体是一个下面是圆柱,上面是圆锥的简单几何体.
圆柱底面直径为4,高为2,圆锥高为3,母线长为=,其表面积为S=πrl+2πrh+πr2=π×2×+8π+4π=2(6+)π(cm2),体积为V=S·h1+S·h2=×π×22×3+π×22×2=12π (cm3).
与立体模型有关的计算
2.拿一张长为a,宽为b的纸,作一圆柱的侧面,用不同的方法作成两种圆柱,画出图形并求这两种圆柱的表面积.(结果保留π)
解:如图,第一种:高为a,表面积为S1=ab+;
第二种:高为b,表面积为S2=ab+.
方法归纳交流 可将a作为圆柱的高,此时底面周长为 ;也可将 作为圆柱的高,此时底面周长为 .
b
b
a
变式演练 图1是一张长为18 cm,宽为12 cm的长方形硬纸板.把它的四个角都剪去一个边长为x cm的小正方形,然后把它折成一个无盖的长方体盒子(如图2),请回答下列问题:
(1)折成的无盖长方体盒子的容积V= cm3.(用含x的代数式表示即可,不需化简)
(2)请完成下表,并根据表格回答,当x取什么正整数时,长方体盒子的容积最大
(3)从正面看折成的长方体盒子,它的形状可能是正方形吗 如果是正方形,求出x的值;如果不是正方形,请说明理由.
x/ cm 1 2 3 4 5
V/ cm3 160 216 80
解:(1)由题意,得长方体盒子的长为(18-2x)、宽为(12-2x)、高为x,因此体积为(18-2x)·(12-2x)·x,
故答案为(18-2x)·(12-2x)·x.
(2)把x=2代入(18-2x)·(12-2x)·x,得(18-2x)·(12-2x)·x=14×8×2=224,
把x=4代入(18-2x)·(12-2x)·x得,(18-2x)·(12-2x)·x=10×4×4=160,
故答案为224,160.
由表可知当x取2时,长方体盒子的容积最大.
(3)它的形状不可能是正方形,理由如下:
当18-2x=x时,即x=6,而当x=6时,图1的短边变为0,因此折不成长方体,故从正面看是正方形是不可能的.
