3.2.1一元一次方程的应用-等积与行程问题 课件(共18张PPT) 2023年—2024学年沪科版数学七年级上册
文档属性
| 名称 | 3.2.1一元一次方程的应用-等积与行程问题 课件(共18张PPT) 2023年—2024学年沪科版数学七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-11 22:43:50 | ||
图片预览





文档简介
(共18张PPT)
3.2 一元一次方程的应用
课程讲授
课程导入
巩固练习
课堂总结
第一课时 等积与行程问题
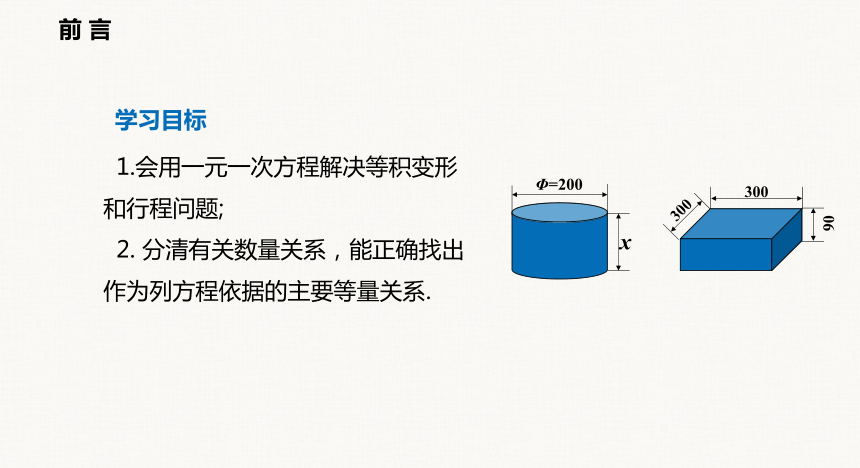
前 言
学习目标
1.会用一元一次方程解决等积变形和行程问题;
2. 分清有关数量关系,能正确找出作为列方程依据的主要等量关系.
x
Φ=200
90
300
300
课程导入
2、路程、平均速度和时间三者的关系.
解:路程=平均速度×时间
回顾
请同学们举手抢答:
1、圆柱体和长方体的体积公式;
做一做:请同学们尝试列出等式.
一支牙膏出口处直径为5mm,小明每次刷牙都挤出1cm长的牙膏,这样一支牙膏可以用36次。该品牌牙膏现推出新包装,只是将出口直径改为6mm,小明还是按习惯每次挤出1cm长的牙膏,这样,这支牙膏能用多少次
课程导入
课程讲授
新课推进
探索 1:等积变形问题
例1
如图,用直径为200mm的圆柱体钢,锻造一个长、宽、高分别为300mm,300mm和90mm的长方体毛坯,应截取多少毫米长的圆柱体钢(计算时π取3.14,结果精确到1mm)?
x
Φ=200
90
300
300
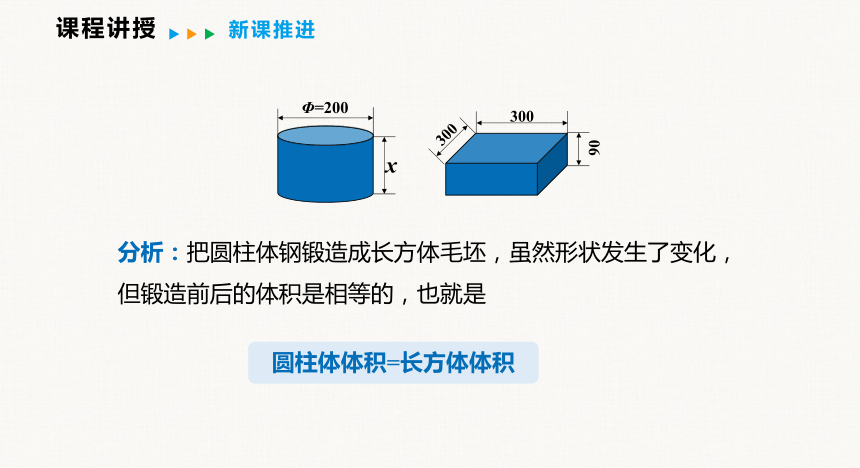
课程讲授
新课推进
x
Φ=200
90
300
300
分析:把圆柱体钢锻造成长方体毛坯,虽然形状发生了变化,但锻造前后的体积是相等的,也就是
圆柱体体积=长方体体积
课程讲授
新课推进
解: 设应截取的圆柱体钢长为 x mm.
根据题意,得
3.14× x =300×300×90
200
2
2
解方程,得 x≈258.
答:应截取约258mm长的圆柱体钢.
课程讲授
新课推进
为了适应经济的发展,铁路运输再次提速.如果客车行驶的平均速度增加40km/h,提速后由合肥到北京1 110 km的路程只需行驶10h.那么提速前,这趟客车平均每时行驶多少千米?
例2
探索 2:行程问题
分析:行程问题中常涉及的量有路程、平均速度、时间.他们之间的基本关系是
路程=平均速度×时间
解: 设提速前客车平均每时行驶x km,
根据题意,得
10(x+40)=1 110
解方程,得 x=71
答:提速前客车的平均速度是71km/h.
课程讲授
新课推进
小结
课程讲授
交流
列方程解应用题有哪些步骤?
审:审清题意,分清题中的已知量和未知量,找出题中的数量关系;
设:设未知数,用未知数表示有关的量;
列:根据题中的相等关系,列一元一次方程。
解:解所列出的一元一次方程;
验.检验所得的值是否正确和符合实际情形;
1
2
3
4
5
6
答:写出答案(包括单位名称)。
巩固练习
习题1
如图,在水平桌面上有甲、乙两个内部呈圆柱形的容器,容器内部的底面积分别为80cm2,100cm2,且甲容器装满水,乙容器是空的.若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲的水位高度低了8cm,求甲的容积为多少?
甲
乙
答:甲的容积为3200cm3.
解方程,得
=3200
解:设甲的容积为xcm3.根据题意,得
甲、乙两站相距480千米,一列慢车从甲站开出,每小时行90千米,一列快车从乙站开出,每小时行140千米.
(1)慢车先开出1小时,快车再开,两车相向而行.问快车开出多少小时后两车相遇?
巩固练习
习题2
解:(1)设快车开出x小时后两车相遇.
等量关系:
慢车行驶距离+快车行驶距离=甲乙两地的距离.
依题意,得 90×1+90x+140x=480.
解方程,得
课程讲授
新课推进
(2)设相背而行y小时两车相距600千米.
等量关系:
慢车行驶距离+快车行驶距离+甲乙两地的距离=600km.
依题意,得 90y+480+140y=600.
(2)两车同时开出,相背而行,多少小时后两车相距600千米?
解方程,得
课程讲授
新课推进
课程讲授
新课推进
(3)设z小时后快车与慢车相距600千米,
等量关系:
快车行驶距离+甲乙两地的距离-慢车行驶距离=600km.
依题意,得 140z+480-90z=600.
(3)两车同时开出,慢车在快车后面同向而行,多少小时后快车与慢车相距600千米?
解方程,得
课程讲授
新课推进
(4)设m小时后快车追上慢车,
等量关系:
慢车行驶距离+甲乙两地的距离=快车行驶距离.
依题意,得 90m+480=140m.
答:略
(4)两车同时开出同向而行,快车在慢车的后面,多少小时后快车追上慢车?
解方程,得
课程总结
小结
用一元一次方程解决问题
步骤
应用
1.设未知数;
2.找等量关系;
3.列方程;
4.解方程;
5.检验作答.
等积变形:变形前后的面(体)积相等
行程问题:
路程=时间×平均速度
直接设元
间接设元
课后作业
课程总结
课后练习1、2、3.
3.2 一元一次方程的应用
课程讲授
课程导入
巩固练习
课堂总结
第一课时 等积与行程问题
前 言
学习目标
1.会用一元一次方程解决等积变形和行程问题;
2. 分清有关数量关系,能正确找出作为列方程依据的主要等量关系.
x
Φ=200
90
300
300
课程导入
2、路程、平均速度和时间三者的关系.
解:路程=平均速度×时间
回顾
请同学们举手抢答:
1、圆柱体和长方体的体积公式;
做一做:请同学们尝试列出等式.
一支牙膏出口处直径为5mm,小明每次刷牙都挤出1cm长的牙膏,这样一支牙膏可以用36次。该品牌牙膏现推出新包装,只是将出口直径改为6mm,小明还是按习惯每次挤出1cm长的牙膏,这样,这支牙膏能用多少次
课程导入
课程讲授
新课推进
探索 1:等积变形问题
例1
如图,用直径为200mm的圆柱体钢,锻造一个长、宽、高分别为300mm,300mm和90mm的长方体毛坯,应截取多少毫米长的圆柱体钢(计算时π取3.14,结果精确到1mm)?
x
Φ=200
90
300
300
课程讲授
新课推进
x
Φ=200
90
300
300
分析:把圆柱体钢锻造成长方体毛坯,虽然形状发生了变化,但锻造前后的体积是相等的,也就是
圆柱体体积=长方体体积
课程讲授
新课推进
解: 设应截取的圆柱体钢长为 x mm.
根据题意,得
3.14× x =300×300×90
200
2
2
解方程,得 x≈258.
答:应截取约258mm长的圆柱体钢.
课程讲授
新课推进
为了适应经济的发展,铁路运输再次提速.如果客车行驶的平均速度增加40km/h,提速后由合肥到北京1 110 km的路程只需行驶10h.那么提速前,这趟客车平均每时行驶多少千米?
例2
探索 2:行程问题
分析:行程问题中常涉及的量有路程、平均速度、时间.他们之间的基本关系是
路程=平均速度×时间
解: 设提速前客车平均每时行驶x km,
根据题意,得
10(x+40)=1 110
解方程,得 x=71
答:提速前客车的平均速度是71km/h.
课程讲授
新课推进
小结
课程讲授
交流
列方程解应用题有哪些步骤?
审:审清题意,分清题中的已知量和未知量,找出题中的数量关系;
设:设未知数,用未知数表示有关的量;
列:根据题中的相等关系,列一元一次方程。
解:解所列出的一元一次方程;
验.检验所得的值是否正确和符合实际情形;
1
2
3
4
5
6
答:写出答案(包括单位名称)。
巩固练习
习题1
如图,在水平桌面上有甲、乙两个内部呈圆柱形的容器,容器内部的底面积分别为80cm2,100cm2,且甲容器装满水,乙容器是空的.若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲的水位高度低了8cm,求甲的容积为多少?
甲
乙
答:甲的容积为3200cm3.
解方程,得
=3200
解:设甲的容积为xcm3.根据题意,得
甲、乙两站相距480千米,一列慢车从甲站开出,每小时行90千米,一列快车从乙站开出,每小时行140千米.
(1)慢车先开出1小时,快车再开,两车相向而行.问快车开出多少小时后两车相遇?
巩固练习
习题2
解:(1)设快车开出x小时后两车相遇.
等量关系:
慢车行驶距离+快车行驶距离=甲乙两地的距离.
依题意,得 90×1+90x+140x=480.
解方程,得
课程讲授
新课推进
(2)设相背而行y小时两车相距600千米.
等量关系:
慢车行驶距离+快车行驶距离+甲乙两地的距离=600km.
依题意,得 90y+480+140y=600.
(2)两车同时开出,相背而行,多少小时后两车相距600千米?
解方程,得
课程讲授
新课推进
课程讲授
新课推进
(3)设z小时后快车与慢车相距600千米,
等量关系:
快车行驶距离+甲乙两地的距离-慢车行驶距离=600km.
依题意,得 140z+480-90z=600.
(3)两车同时开出,慢车在快车后面同向而行,多少小时后快车与慢车相距600千米?
解方程,得
课程讲授
新课推进
(4)设m小时后快车追上慢车,
等量关系:
慢车行驶距离+甲乙两地的距离=快车行驶距离.
依题意,得 90m+480=140m.
答:略
(4)两车同时开出同向而行,快车在慢车的后面,多少小时后快车追上慢车?
解方程,得
课程总结
小结
用一元一次方程解决问题
步骤
应用
1.设未知数;
2.找等量关系;
3.列方程;
4.解方程;
5.检验作答.
等积变形:变形前后的面(体)积相等
行程问题:
路程=时间×平均速度
直接设元
间接设元
课后作业
课程总结
课后练习1、2、3.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
