第六章反比例函数(单元测试) 北师大版数学九年级上册(含答案)
文档属性
| 名称 | 第六章反比例函数(单元测试) 北师大版数学九年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 441.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-11 23:03:15 | ||
图片预览


文档简介
第六章反比例函数(单元测试)
2023-2024学年九年级上册数学北师大版
一、单选题(共10小题,满分40分)
1.学校课外生物小组的同学准备自己动手,用旧围栏建一个面积为平方米的矩形饲养场.设它的一边长为(米),那么另一边的长(米)与(米)的函数图象大致是( )
A. B. C. D.
2.如图,在平面直角坐标系中,函数y=kx与的图象交于A,B两点,过点B作y轴的平行线,交函数的图象于点C,连接AC,则△ABC的面积为( )
A.2.5 B.5 C.6 D.10
3.定义:[a,b]为反比例函数y=(ab≠0,a,b为实数)的“关联数”.反比例函数y=的“关联数”为[m,m+2],反比例函数y=的“关联数”为[m+1,m+3],若m>0,则 ( )
A.k1=k2 B.k1>k2
C.k14.关于函数,下列说法中错误的是( ).
A.函数的图象在第二、四象限 B.的值随值的增大而减小
C.函数的图象与坐标轴没有交点 D.函数的图象关于原点对称
5.已知点A(a,b)是一次函数y=-x+4和反比例函数y=的一个交点,则代数式a2+b2的值为( )
A.8 B.10 C.12 D.14
6.若都在函数的图像上,则( )
A. B. C. D.
7.在函数y(m为常数)的图象上有三点(﹣4,y1),(﹣2,y2),(1,y3),则函数值y1,y2,y3的大小关系为( )
A.y2<y1<y3 B.y1<y2<y3 C.y3<y2<y1 D.y3<y1<y2
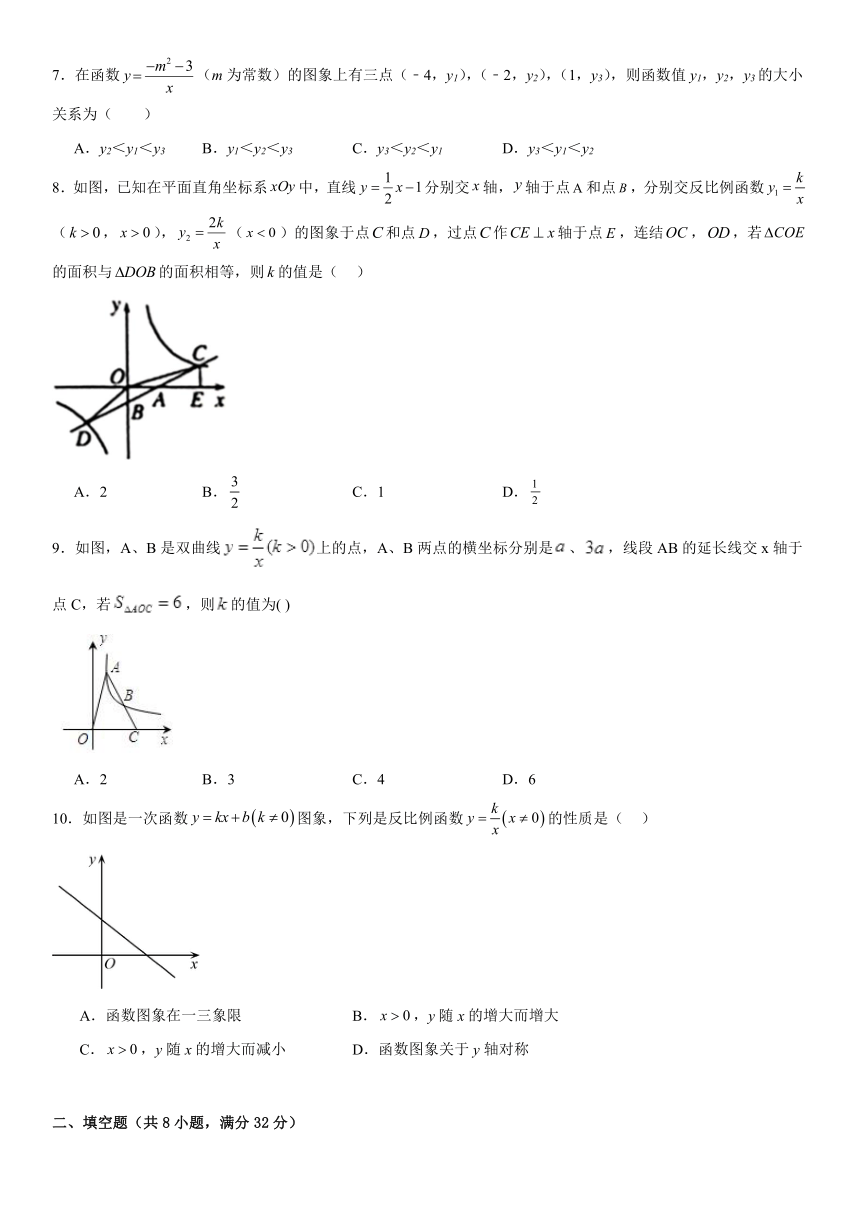
8.如图,已知在平面直角坐标系中,直线分别交轴,轴于点和点,分别交反比例函数(,),()的图象于点和点,过点作轴于点,连结,,若的面积与的面积相等,则的值是( )
A.2 B. C.1 D.
9.如图,A、B是双曲线上的点,A、B两点的横坐标分别是、,线段AB的延长线交x轴于点C,若,则的值为( )
A.2 B.3 C.4 D.6
10.如图是一次函数图象,下列是反比例函数的性质是( )
A.函数图象在一三象限 B.,y随x的增大而增大
C.,y随x的增大而减小 D.函数图象关于y轴对称
二、填空题(共8小题,满分32分)
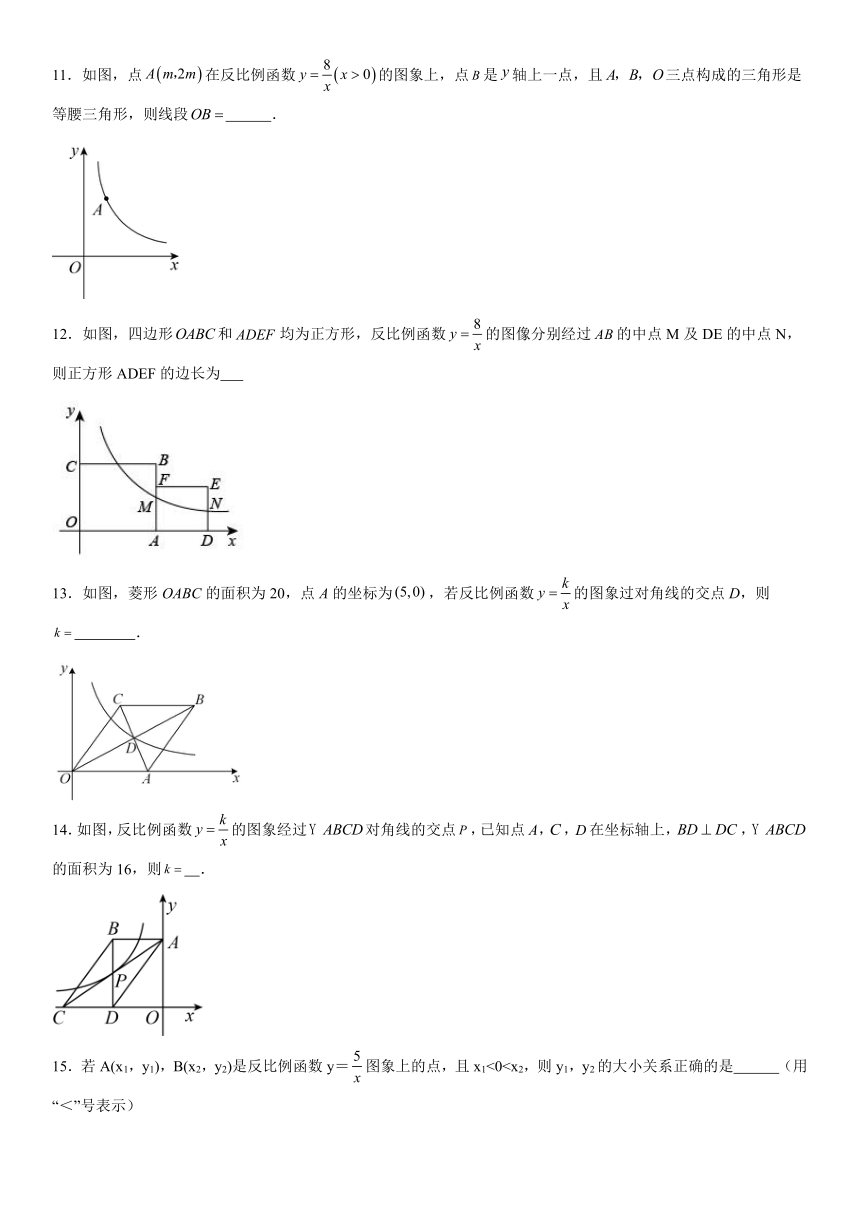
11.如图,点在反比例函数的图象上,点是轴上一点,且三点构成的三角形是等腰三角形,则线段 .
12.如图,四边形和均为正方形,反比例函数的图像分别经过的中点M及DE的中点N,则正方形ADEF的边长为
13.如图,菱形OABC的面积为20,点A的坐标为,若反比例函数的图象过对角线的交点D,则 .
14.如图,反比例函数的图象经过对角线的交点,已知点A,,在坐标轴上,,的面积为16,则 .
15.若A(x1,y1),B(x2,y2)是反比例函数y=图象上的点,且x1<016.在直角坐标系中,函数y=(x>0,k为常数)的图象经过A(4,1),点B(a,b)(0<a<4)是双曲线上的一动点,过A作AC⊥y轴于C,点D是坐标系中的另一点.若以A.B.C.D为顶点的平行四边形的面积为12,那么对角线长度的最大值为 .
17.如图,在平面直角坐标系中,点在函数的图象上,过点分别作轴、轴的垂线,垂足分别为,取线段的中点,连结并延长交轴于点,则的面积为 .
18.某标准游泳池的尺寸为长米,宽米,深度为3米,游泳池蓄水能游泳时,水深不低于米.
(1)游泳池的排水管每小时排水立方米,那么将游泳池最低蓄水量排完用了小时.
①写出与的函数关系式为 ;
②当时,的值为 ;
(2)在(1)的情况下,如果最低蓄水量排完不超过5小时,每小时排水量最少增加 立方米.
三、解答题(共6小题,每题8分,满分48分)
19.如图在平面直角坐标系中,直线与反比例函数在第二象限内的图象交于点,与轴交于点,连接.
(1)求反比例函数的解析式;
(2)直接写出的解集;
(3)将直线沿着射线平移个单位得到直线,直线与交于点,为反比例函数图象上一点,当时求点的横坐标.
20.如图,边长为2的正方形的顶点分别在x轴、y轴上,函数的图象经过点B,把正方形沿翻折得到正方形,交这个函数的图象于点E,连接.
(1)求k的值;
(2)求四边形的面积.
21.如图,在平面直角坐标系中,一次函数与反比例函数交于点,.
(1)求,对应的函数表达式;
(2)直接写出当时,不等式的解集.
(3)若点P是反比例函数图像上一点,且的面积是的面积的2倍,求点P的横坐标.
22.如图,一次函数的图象与反比例函数的图象相交于A、B两点.
(1)利用图中条件,求反比例函数与一次函数的关系式;
(2)根据图象写出使该一次函数的值大于该反比例函数的值的的取值范围;
(3)过B点作BH垂直于轴垂足为H,连接OB,在轴是否存在一点P(不与点O重合),使得以P、B、H为顶点的三角形与△BHO相似;若存在,直接写出点P的坐标;不存在,说明理由.
23.在面积为定值的一组菱形中,当菱形的一条对角线长为4cm时,它的另一条对角线长为12cm.
(1)设菱形的两条对角线长分别为x(cm)和y(cm),求y关于x的函数解析式.
(2)若其中一个菱形的一条对角线长为6cm,求这个菱形的边长.
(3)小杭同学说:这个菱形的两条对角线长的和可以为13cm.小杭的说法正确吗?请说明理由.
24.如图,在左边托盘A(固定)中放置一个生物,在右边托盘B(可左右移动)中放置一定重量的砝码,可使得仪器左右平衡,改变托盘B与支撑点M的跳高,记录相应的托盘B中的砝码质量,得到下表:
托盘B与点M的距离x(cm) 10 15 20 25 30
托盘B中的砝码质量y(g) 30 20 15 12 10
(1)把上表中(x,y)的各级对应值作为点的坐标,在如图所示的平面直角坐标系中描出其余的点,并用一条光滑的曲线连接起来,观察所画的图象,猜想y与x的函数关系,求出该函数关系式.
(2)当托盘B向左移动(不能超过点M)时,应往托盘B中添加砝码还是减少砝码?为什么?
参考答案:
1.C
2.B
3.C
4.B
5.D
6.A
7.D
8.A
9.B
10.B
11.或或8
12..
13.8
14.
15.y1<y2
16.
17.6
18.
19.(1)
(2)或
(3)或
20.(1)4
(2)3
21.(1),
(2)
(3)或2或 或
22.(1),(2)(3)存在,P1(2,0) P2(5,0) P3(-3,0)
23.(1)
(2)5
(3)不正确
24.(1)反比例函数关系,;(2)添加砝码
2023-2024学年九年级上册数学北师大版
一、单选题(共10小题,满分40分)
1.学校课外生物小组的同学准备自己动手,用旧围栏建一个面积为平方米的矩形饲养场.设它的一边长为(米),那么另一边的长(米)与(米)的函数图象大致是( )
A. B. C. D.
2.如图,在平面直角坐标系中,函数y=kx与的图象交于A,B两点,过点B作y轴的平行线,交函数的图象于点C,连接AC,则△ABC的面积为( )
A.2.5 B.5 C.6 D.10
3.定义:[a,b]为反比例函数y=(ab≠0,a,b为实数)的“关联数”.反比例函数y=的“关联数”为[m,m+2],反比例函数y=的“关联数”为[m+1,m+3],若m>0,则 ( )
A.k1=k2 B.k1>k2
C.k1
A.函数的图象在第二、四象限 B.的值随值的增大而减小
C.函数的图象与坐标轴没有交点 D.函数的图象关于原点对称
5.已知点A(a,b)是一次函数y=-x+4和反比例函数y=的一个交点,则代数式a2+b2的值为( )
A.8 B.10 C.12 D.14
6.若都在函数的图像上,则( )
A. B. C. D.
7.在函数y(m为常数)的图象上有三点(﹣4,y1),(﹣2,y2),(1,y3),则函数值y1,y2,y3的大小关系为( )
A.y2<y1<y3 B.y1<y2<y3 C.y3<y2<y1 D.y3<y1<y2
8.如图,已知在平面直角坐标系中,直线分别交轴,轴于点和点,分别交反比例函数(,),()的图象于点和点,过点作轴于点,连结,,若的面积与的面积相等,则的值是( )
A.2 B. C.1 D.
9.如图,A、B是双曲线上的点,A、B两点的横坐标分别是、,线段AB的延长线交x轴于点C,若,则的值为( )
A.2 B.3 C.4 D.6
10.如图是一次函数图象,下列是反比例函数的性质是( )
A.函数图象在一三象限 B.,y随x的增大而增大
C.,y随x的增大而减小 D.函数图象关于y轴对称
二、填空题(共8小题,满分32分)
11.如图,点在反比例函数的图象上,点是轴上一点,且三点构成的三角形是等腰三角形,则线段 .
12.如图,四边形和均为正方形,反比例函数的图像分别经过的中点M及DE的中点N,则正方形ADEF的边长为
13.如图,菱形OABC的面积为20,点A的坐标为,若反比例函数的图象过对角线的交点D,则 .
14.如图,反比例函数的图象经过对角线的交点,已知点A,,在坐标轴上,,的面积为16,则 .
15.若A(x1,y1),B(x2,y2)是反比例函数y=图象上的点,且x1<0
17.如图,在平面直角坐标系中,点在函数的图象上,过点分别作轴、轴的垂线,垂足分别为,取线段的中点,连结并延长交轴于点,则的面积为 .
18.某标准游泳池的尺寸为长米,宽米,深度为3米,游泳池蓄水能游泳时,水深不低于米.
(1)游泳池的排水管每小时排水立方米,那么将游泳池最低蓄水量排完用了小时.
①写出与的函数关系式为 ;
②当时,的值为 ;
(2)在(1)的情况下,如果最低蓄水量排完不超过5小时,每小时排水量最少增加 立方米.
三、解答题(共6小题,每题8分,满分48分)
19.如图在平面直角坐标系中,直线与反比例函数在第二象限内的图象交于点,与轴交于点,连接.
(1)求反比例函数的解析式;
(2)直接写出的解集;
(3)将直线沿着射线平移个单位得到直线,直线与交于点,为反比例函数图象上一点,当时求点的横坐标.
20.如图,边长为2的正方形的顶点分别在x轴、y轴上,函数的图象经过点B,把正方形沿翻折得到正方形,交这个函数的图象于点E,连接.
(1)求k的值;
(2)求四边形的面积.
21.如图,在平面直角坐标系中,一次函数与反比例函数交于点,.
(1)求,对应的函数表达式;
(2)直接写出当时,不等式的解集.
(3)若点P是反比例函数图像上一点,且的面积是的面积的2倍,求点P的横坐标.
22.如图,一次函数的图象与反比例函数的图象相交于A、B两点.
(1)利用图中条件,求反比例函数与一次函数的关系式;
(2)根据图象写出使该一次函数的值大于该反比例函数的值的的取值范围;
(3)过B点作BH垂直于轴垂足为H,连接OB,在轴是否存在一点P(不与点O重合),使得以P、B、H为顶点的三角形与△BHO相似;若存在,直接写出点P的坐标;不存在,说明理由.
23.在面积为定值的一组菱形中,当菱形的一条对角线长为4cm时,它的另一条对角线长为12cm.
(1)设菱形的两条对角线长分别为x(cm)和y(cm),求y关于x的函数解析式.
(2)若其中一个菱形的一条对角线长为6cm,求这个菱形的边长.
(3)小杭同学说:这个菱形的两条对角线长的和可以为13cm.小杭的说法正确吗?请说明理由.
24.如图,在左边托盘A(固定)中放置一个生物,在右边托盘B(可左右移动)中放置一定重量的砝码,可使得仪器左右平衡,改变托盘B与支撑点M的跳高,记录相应的托盘B中的砝码质量,得到下表:
托盘B与点M的距离x(cm) 10 15 20 25 30
托盘B中的砝码质量y(g) 30 20 15 12 10
(1)把上表中(x,y)的各级对应值作为点的坐标,在如图所示的平面直角坐标系中描出其余的点,并用一条光滑的曲线连接起来,观察所画的图象,猜想y与x的函数关系,求出该函数关系式.
(2)当托盘B向左移动(不能超过点M)时,应往托盘B中添加砝码还是减少砝码?为什么?
参考答案:
1.C
2.B
3.C
4.B
5.D
6.A
7.D
8.A
9.B
10.B
11.或或8
12..
13.8
14.
15.y1<y2
16.
17.6
18.
19.(1)
(2)或
(3)或
20.(1)4
(2)3
21.(1),
(2)
(3)或2或 或
22.(1),(2)(3)存在,P1(2,0) P2(5,0) P3(-3,0)
23.(1)
(2)5
(3)不正确
24.(1)反比例函数关系,;(2)添加砝码
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
