第24章 圆 单元检测 2023-2024学年人教版数学九年级上册(无答案)
文档属性
| 名称 | 第24章 圆 单元检测 2023-2024学年人教版数学九年级上册(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 299.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-11 23:40:15 | ||
图片预览

文档简介
第24章 圆 单元检测 2023-2024学年人教版数学九年级上册
一、单选题
1.如图,△ABC的顶点A,B,C均在⊙O上,若∠ABC+∠AOC=75°,则∠OAC的大小是( )
A.25° B.50° C.65° D.75°
2.如图,已知△ABC中,AB=2,BC=3,∠B=90°,以点B为圆心作半径为r的⊙B,要使点A,C在⊙B外,则r的取值范围是( )
A.0<r<2 B.0<r<3 C.2<r<3 D.r>3
3.已知⊙O的直径为4cm.若点P到圆心O的距离为3cm,则点P( )
A.在⊙O上 B.在⊙O内 C.在⊙O外 D.无法确定
4.如图,正六边形ABCDEF内接于⊙O,点P是 上的任意一点,则∠APB的大小是( )
A.15° B.30° C.45° D.60°
5.如图,AD是⊙O的直径,PA,PB分别切⊙O于点A,B,弦BC∥AD.当的度数为126°时,则∠P的度数为( )
A.54° B.55° C.63° D.64°
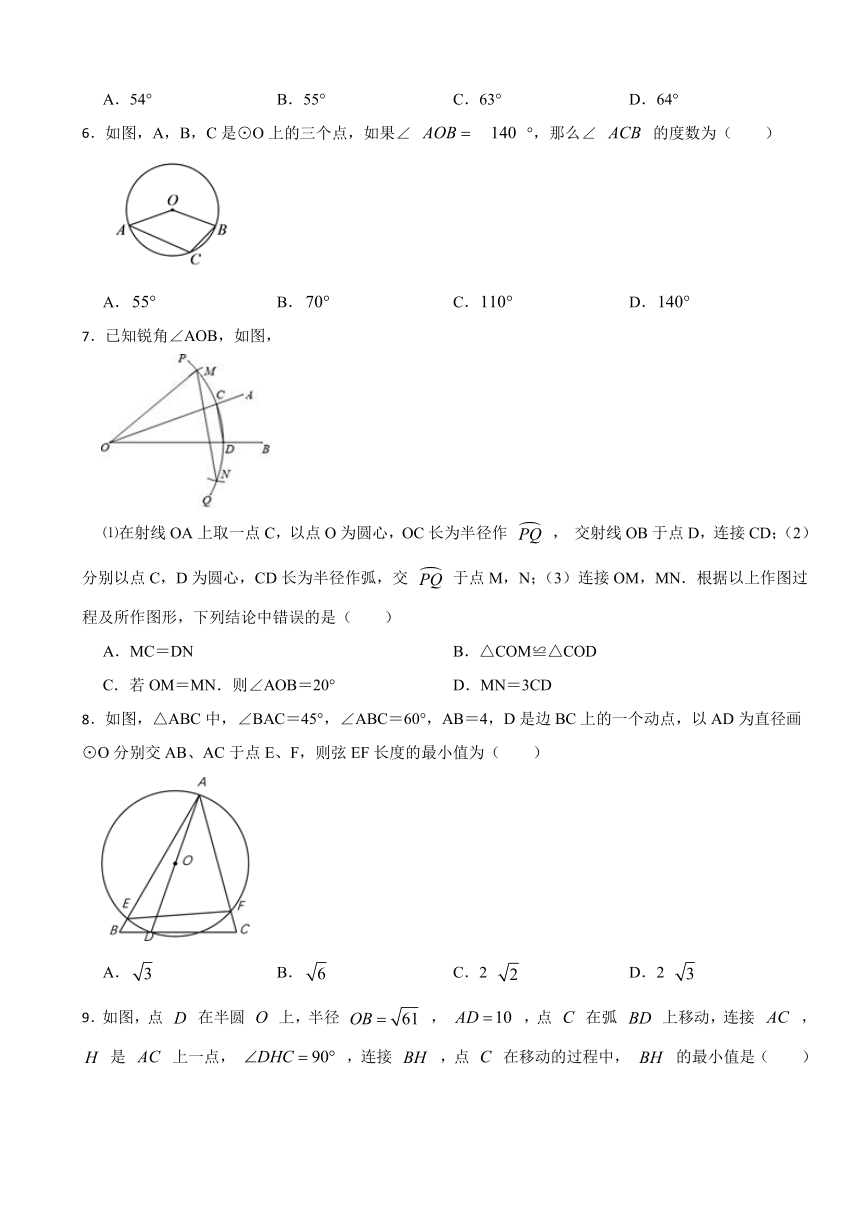
6.如图,A,B,C是⊙O上的三个点,如果∠ °,那么∠ 的度数为( )
A. B. C. D.
7.已知锐角∠AOB,如图,
⑴在射线OA上取一点C,以点O为圆心,OC长为半径作 , 交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交 于点M,N;(3)连接OM,MN.根据以上作图过程及所作图形,下列结论中错误的是( )
A.MC=DN B.△COM≌△COD
C.若OM=MN.则∠AOB=20° D.MN=3CD
8.如图,△ABC中,∠BAC=45°,∠ABC=60°,AB=4,D是边BC上的一个动点,以AD为直径画⊙O分别交AB、AC于点E、F,则弦EF长度的最小值为( )
A. B. C.2 D.2
9.如图,点 在半圆 上,半径 , ,点 在弧 上移动,连接 , 是 上一点, ,连接 ,点 在移动的过程中, 的最小值是( )
A.5 B.6 C.7 D.8
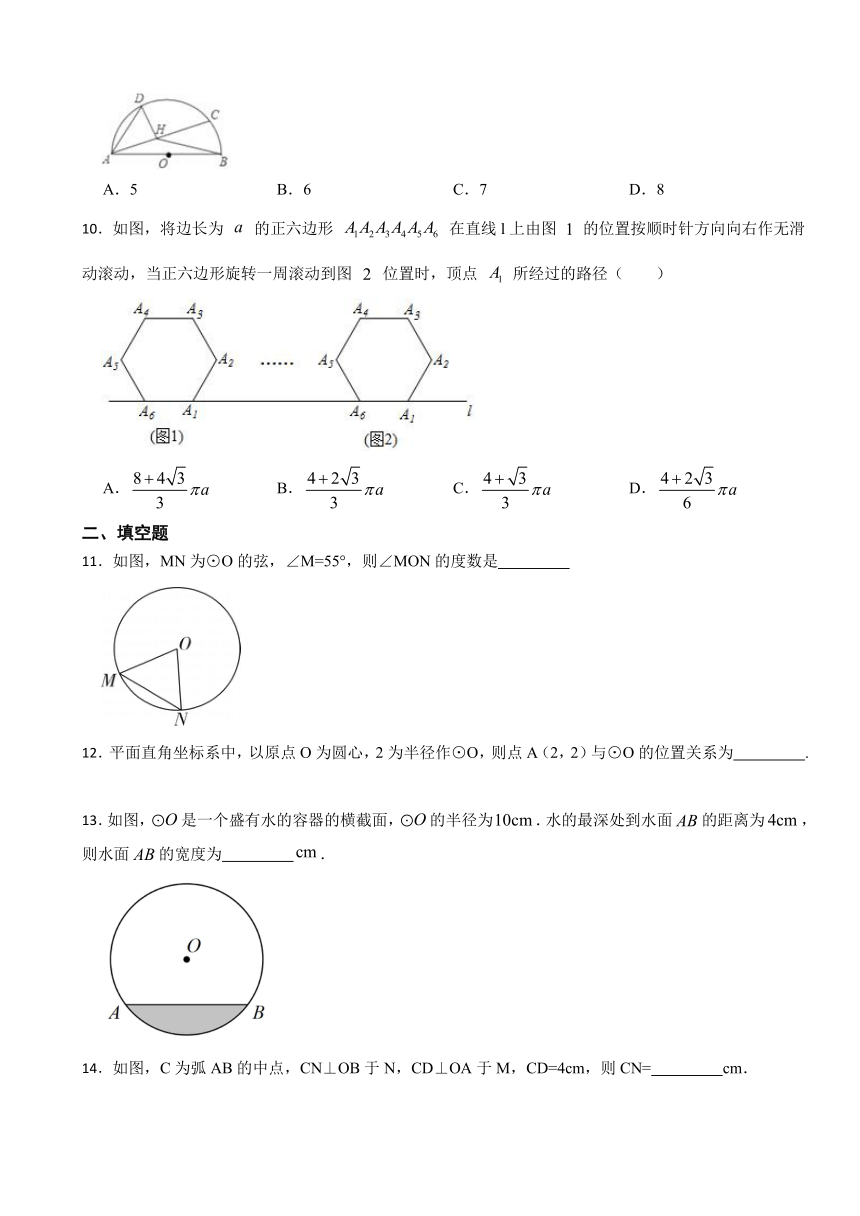
10.如图,将边长为 的正六边形 在直线l上由图 的位置按顺时针方向向右作无滑动滚动,当正六边形旋转一周滚动到图 位置时,顶点 所经过的路径( )
A. B. C. D.
二、填空题
11.如图,MN为⊙O的弦,∠M=55°,则∠MON的度数是
12.平面直角坐标系中,以原点O为圆心,2为半径作⊙O,则点A(2,2)与⊙O的位置关系为 .
13.如图,是一个盛有水的容器的横截面,的半径为.水的最深处到水面的距离为,则水面的宽度为 .
14.如图,C为弧AB的中点,CN⊥OB于N,CD⊥OA于M,CD=4cm,则CN= cm.
15.如图,已知射线 ,点 从B点出发,以每秒1个单位长度沿射线 向右运动;同时射线 绕点 顺时针旋转一周,当射线 停止运动时,点 随之停止运动.以 为圆心,1个单位长度为半径画圆,若运动两秒后,射线 与 恰好有且只有一个公共点,则射线 旋转的速度为每秒 度.
三、解答题
16.如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作AC的垂线交AC于点E,交AB的延长线于点F.
(1)求证:DE与⊙O相切;
(2)若CD=BF,AE=3,求DF的长.
17.如图,△ABC内接于⊙O,∠A=45°,⊙O的半径为5,求BC的长.
18.如图,PA,PB是⊙O的切线,点A,B为切点,AC是⊙O的直径,∠ACB=70°,求∠APB的度数.
19.如图,将一个两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D,E,量出半径OC=5cm,弦DE=8cm,求直尺的宽.
20.如图,学校某处空地上有A、B、C三棵树,现准备建一个圆形景观鱼池,要求A、B、C三棵树恰在圆周上,请你帮助设计鱼池,在图中作出它的鱼池轮廓,保留作图痕迹并将圆心标记为点O.
21.已知内接于,为的直径,N为的中点,连接交于点H.
(1)如图①,求证;
(2)如图②,点D在上,连接,,,交于点E,若,求证;
(3)如图③,在(2)的条件下,点F在上,过点F作,交于点G.,过点F作,垂足为R,连接,,,点T在的延长线上,连接,过点T作,交的延长线于点M,若,求的长.
一、单选题
1.如图,△ABC的顶点A,B,C均在⊙O上,若∠ABC+∠AOC=75°,则∠OAC的大小是( )
A.25° B.50° C.65° D.75°
2.如图,已知△ABC中,AB=2,BC=3,∠B=90°,以点B为圆心作半径为r的⊙B,要使点A,C在⊙B外,则r的取值范围是( )
A.0<r<2 B.0<r<3 C.2<r<3 D.r>3
3.已知⊙O的直径为4cm.若点P到圆心O的距离为3cm,则点P( )
A.在⊙O上 B.在⊙O内 C.在⊙O外 D.无法确定
4.如图,正六边形ABCDEF内接于⊙O,点P是 上的任意一点,则∠APB的大小是( )
A.15° B.30° C.45° D.60°
5.如图,AD是⊙O的直径,PA,PB分别切⊙O于点A,B,弦BC∥AD.当的度数为126°时,则∠P的度数为( )
A.54° B.55° C.63° D.64°
6.如图,A,B,C是⊙O上的三个点,如果∠ °,那么∠ 的度数为( )
A. B. C. D.
7.已知锐角∠AOB,如图,
⑴在射线OA上取一点C,以点O为圆心,OC长为半径作 , 交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交 于点M,N;(3)连接OM,MN.根据以上作图过程及所作图形,下列结论中错误的是( )
A.MC=DN B.△COM≌△COD
C.若OM=MN.则∠AOB=20° D.MN=3CD
8.如图,△ABC中,∠BAC=45°,∠ABC=60°,AB=4,D是边BC上的一个动点,以AD为直径画⊙O分别交AB、AC于点E、F,则弦EF长度的最小值为( )
A. B. C.2 D.2
9.如图,点 在半圆 上,半径 , ,点 在弧 上移动,连接 , 是 上一点, ,连接 ,点 在移动的过程中, 的最小值是( )
A.5 B.6 C.7 D.8
10.如图,将边长为 的正六边形 在直线l上由图 的位置按顺时针方向向右作无滑动滚动,当正六边形旋转一周滚动到图 位置时,顶点 所经过的路径( )
A. B. C. D.
二、填空题
11.如图,MN为⊙O的弦,∠M=55°,则∠MON的度数是
12.平面直角坐标系中,以原点O为圆心,2为半径作⊙O,则点A(2,2)与⊙O的位置关系为 .
13.如图,是一个盛有水的容器的横截面,的半径为.水的最深处到水面的距离为,则水面的宽度为 .
14.如图,C为弧AB的中点,CN⊥OB于N,CD⊥OA于M,CD=4cm,则CN= cm.
15.如图,已知射线 ,点 从B点出发,以每秒1个单位长度沿射线 向右运动;同时射线 绕点 顺时针旋转一周,当射线 停止运动时,点 随之停止运动.以 为圆心,1个单位长度为半径画圆,若运动两秒后,射线 与 恰好有且只有一个公共点,则射线 旋转的速度为每秒 度.
三、解答题
16.如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作AC的垂线交AC于点E,交AB的延长线于点F.
(1)求证:DE与⊙O相切;
(2)若CD=BF,AE=3,求DF的长.
17.如图,△ABC内接于⊙O,∠A=45°,⊙O的半径为5,求BC的长.
18.如图,PA,PB是⊙O的切线,点A,B为切点,AC是⊙O的直径,∠ACB=70°,求∠APB的度数.
19.如图,将一个两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D,E,量出半径OC=5cm,弦DE=8cm,求直尺的宽.
20.如图,学校某处空地上有A、B、C三棵树,现准备建一个圆形景观鱼池,要求A、B、C三棵树恰在圆周上,请你帮助设计鱼池,在图中作出它的鱼池轮廓,保留作图痕迹并将圆心标记为点O.
21.已知内接于,为的直径,N为的中点,连接交于点H.
(1)如图①,求证;
(2)如图②,点D在上,连接,,,交于点E,若,求证;
(3)如图③,在(2)的条件下,点F在上,过点F作,交于点G.,过点F作,垂足为R,连接,,,点T在的延长线上,连接,过点T作,交的延长线于点M,若,求的长.
同课章节目录
