直线与平面平行的判定
图片预览


文档简介
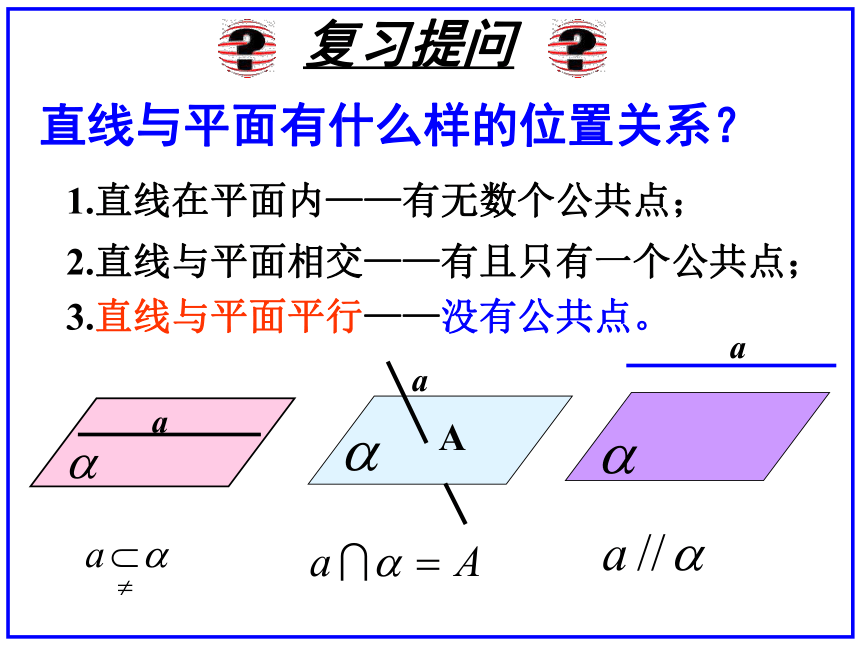
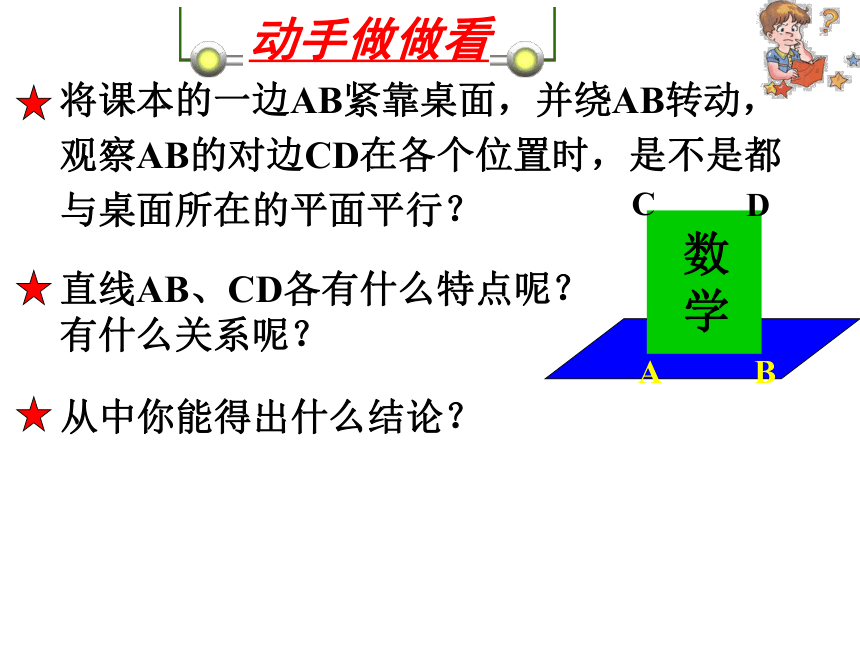
课件19张PPT。林启恩纪念中学教师 : 庄思佳汉滨高级中学§5.1.1 直线与平面平行的判定αa复习提问直线与平面有什么样的位置关系?1.直线在平面内——有无数个公共点;2.直线与平面相交——有且只有一个公共点;3.直线与平面平行——没有公共点。动手做做看将课本的一边AB紧靠桌面,并绕AB转动,观察AB的对边CD在各个位置时,是不是都与桌面所在的平面平行?从中你能得出什么结论?直线AB、CD各有什么特点呢?
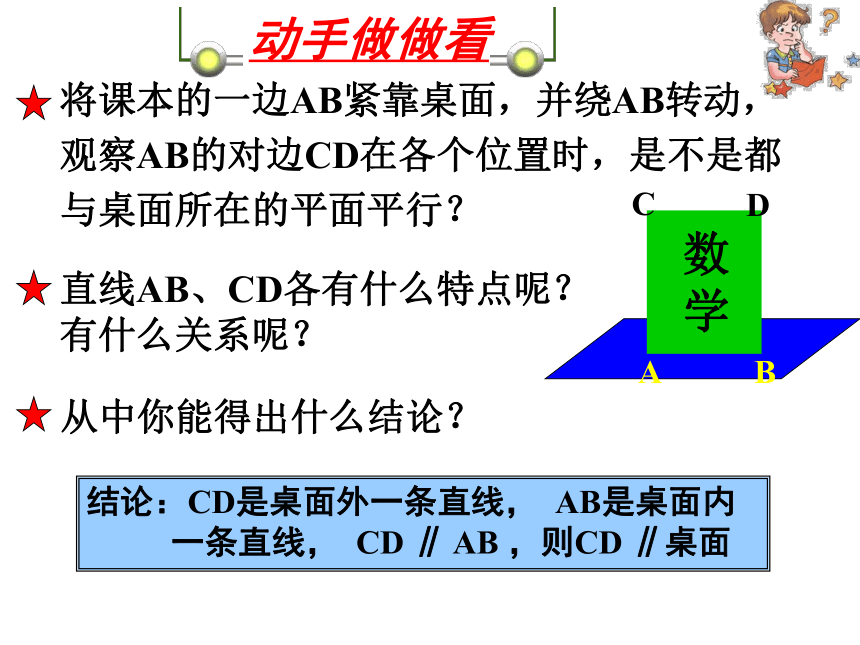
有什么关系呢?数学将课本的一边AB紧靠桌面,并绕AB转动,观察AB的对边CD在各个位置时,是不是都与桌面所在的平面平行?结论:CD是桌面外一条直线, AB是桌面内
一条直线, CD ∥ AB ,则CD ∥桌面从中你能得出什么结论?动手做做看直线AB、CD各有什么特点呢?
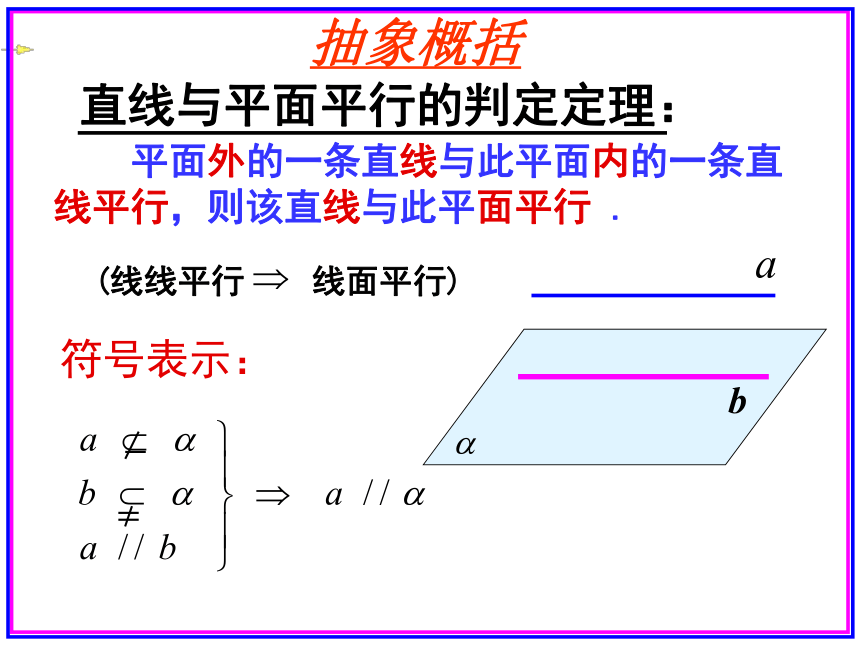
有什么关系呢?符号表示: b抽象概括(线线平行 线面平行) 平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行 .感受校园生活中线面平行的例子:天花板平面ab感受校园生活中线面平行的例子:球场地面1、判断说法是否正确:(1) 如果一条直线不在平面内,则这条直线就与这个
平面平行。 ( )(2) 过直线外一点,可以作无数个平面与这条直线
平行。 ( ) 如果一条直线平行平面内的一条直线,则这条直线
平行于此平面。 ( )╳√
╳练习1: 可知EF在面BCD外,而E,F分别为
AB,AD的中点,即EF为△ABD的中位线,所以可
得EF//BD,又BD在面BCD内,故EF//面BCD。 例1. 如图,空间四边形ABCD中,
E、F分别是 AB,AD的中点.
判断EF与平面BCD的位置关系.定理的应用 分析:连接BD. 解:连结BD.∵AE=EB,AF=FD
∴EF∥BD(三角形中位线性质) 小结:判断线面平行,先找线线平行定理的应用 例1. 如图,空间四边形ABCD中,
E、F分别是 AB,AD的中点.
判断EF与平面BCD的位置关系.EF//平面BCD变式:如图,在空间四边形ABCD中,E、F分
别为AB、AD上的点,若 ,则EF
与平面BCD的位置关系是_____________. 例2.如图所示,空间四边形ABCD
中, E、F、G、H分别是AB、BC、
CD、AD的中点。试指出图中满足
线面平行位置关系的所有情况。定理的应用分析:此题是直线与平面平行判定定理的应用,
要找出线面平行的位置关系首先得找是
否存在线线平行。定理的应用解:由EF//GH//AC,得
(1)EF//平面ACD;
(2)AC//平面EFGH;
(3)HG//平面ABC. 由BD//EH//FG,得
(4)BD//平面EFGH;
(5)EH//平面BCD;
(6)FG//平面ABD. 小结:要找线面平行,先找线线平行例2.如图所示,空间四边形ABCD
中, E、F、G、H分别是AB、BC、
CD、AD的中点。试指出图中满足
线面平行位置关系的所有情况。(1)与直线AB平行的平面是:(2)与直线AC平行的平面是:2、如图,长方体的六个面都是矩形,则练习2:练习3: 3.如图,四棱锥A—DBCE中,
O为底面正方形DBCE对角线
的交点,F为AE的中点.
求证:AB//平面DCF. 分析:要证明AB//平面DCF,只需要在平面DCF中找一条
直线与AB平行即可。 提示:要证BD1//平面
AEC即要在平面AEC内找
一条直线与BD1平行.根据
已知条件考虑应该怎样作
辅助线?思考题: 如图,正方体ABCD-A1B1C1D1中,E为DD1的
中点,求证:BD1//平面AEC.O归纳小结1.判定直线与平面平行的方法:(1)定义法:直线与平面没有公共点则线面平行;(2)判定定理:(线线平行 线面平行);2.用定理证明线面平行时,在寻找平行直线可以通过 三角形的中位线、梯形的中位线、平行线的判定等来完成。 3.证明的书写三个条件“内”、“外”、“平行”,缺一
不可。作业:课本P36第4题再见!
有什么关系呢?数学将课本的一边AB紧靠桌面,并绕AB转动,观察AB的对边CD在各个位置时,是不是都与桌面所在的平面平行?结论:CD是桌面外一条直线, AB是桌面内
一条直线, CD ∥ AB ,则CD ∥桌面从中你能得出什么结论?动手做做看直线AB、CD各有什么特点呢?
有什么关系呢?符号表示: b抽象概括(线线平行 线面平行) 平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行 .感受校园生活中线面平行的例子:天花板平面ab感受校园生活中线面平行的例子:球场地面1、判断说法是否正确:(1) 如果一条直线不在平面内,则这条直线就与这个
平面平行。 ( )(2) 过直线外一点,可以作无数个平面与这条直线
平行。 ( ) 如果一条直线平行平面内的一条直线,则这条直线
平行于此平面。 ( )╳√
╳练习1: 可知EF在面BCD外,而E,F分别为
AB,AD的中点,即EF为△ABD的中位线,所以可
得EF//BD,又BD在面BCD内,故EF//面BCD。 例1. 如图,空间四边形ABCD中,
E、F分别是 AB,AD的中点.
判断EF与平面BCD的位置关系.定理的应用 分析:连接BD. 解:连结BD.∵AE=EB,AF=FD
∴EF∥BD(三角形中位线性质) 小结:判断线面平行,先找线线平行定理的应用 例1. 如图,空间四边形ABCD中,
E、F分别是 AB,AD的中点.
判断EF与平面BCD的位置关系.EF//平面BCD变式:如图,在空间四边形ABCD中,E、F分
别为AB、AD上的点,若 ,则EF
与平面BCD的位置关系是_____________. 例2.如图所示,空间四边形ABCD
中, E、F、G、H分别是AB、BC、
CD、AD的中点。试指出图中满足
线面平行位置关系的所有情况。定理的应用分析:此题是直线与平面平行判定定理的应用,
要找出线面平行的位置关系首先得找是
否存在线线平行。定理的应用解:由EF//GH//AC,得
(1)EF//平面ACD;
(2)AC//平面EFGH;
(3)HG//平面ABC. 由BD//EH//FG,得
(4)BD//平面EFGH;
(5)EH//平面BCD;
(6)FG//平面ABD. 小结:要找线面平行,先找线线平行例2.如图所示,空间四边形ABCD
中, E、F、G、H分别是AB、BC、
CD、AD的中点。试指出图中满足
线面平行位置关系的所有情况。(1)与直线AB平行的平面是:(2)与直线AC平行的平面是:2、如图,长方体的六个面都是矩形,则练习2:练习3: 3.如图,四棱锥A—DBCE中,
O为底面正方形DBCE对角线
的交点,F为AE的中点.
求证:AB//平面DCF. 分析:要证明AB//平面DCF,只需要在平面DCF中找一条
直线与AB平行即可。 提示:要证BD1//平面
AEC即要在平面AEC内找
一条直线与BD1平行.根据
已知条件考虑应该怎样作
辅助线?思考题: 如图,正方体ABCD-A1B1C1D1中,E为DD1的
中点,求证:BD1//平面AEC.O归纳小结1.判定直线与平面平行的方法:(1)定义法:直线与平面没有公共点则线面平行;(2)判定定理:(线线平行 线面平行);2.用定理证明线面平行时,在寻找平行直线可以通过 三角形的中位线、梯形的中位线、平行线的判定等来完成。 3.证明的书写三个条件“内”、“外”、“平行”,缺一
不可。作业:课本P36第4题再见!
