第三章 一元一次方程单元检测试题2(含答案)
文档属性
| 名称 | 第三章 一元一次方程单元检测试题2(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 265.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-11 19:07:47 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第三章《一元一次方程》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(共10小题,每题3分,满分30分)
1.下列运用等式的性质进行的变形,不正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.方程x﹣2=2﹣x的解是( )
A.x=1 B.x=﹣1 C.x=2 D.x=0
3.已知式子的值与互为倒数,那么x的值是( )
A.6 B. C. D.5
4.三个正整数的比是,它们的和是,那么这三个数中最大的数是( )
A.56 B.48 C.36 D.12
5.如果是关于的方程的解,则值为( )
A. B. C. D.
6.下列表述正确的是( )
A.由,得 B.由,得
C.由,得 D.由,得
7.若与互为相反数,则a的值为( )
A. B. C. D.
8.已知x=2是关于x的一元一次方程mx+2=0的解,则m的值为( )
A.﹣1 B.0 C.1 D.2
9.某项工作甲单独做需4天完成,乙单独做需6天完成,若甲先做了一天,然后甲、乙合作完成此项工作,若设甲一共做了天,所列方程为( )
A. B. C. D.
10.干墨鱼用水浸泡后,重量可增加210%,某加工单位准备为某饭店提供湿墨鱼,问需要多少干墨鱼做原料?用x表示所需干墨鱼的数,则下列方程正确的是( ).
A. B. C. D.
二、填空题(每题3分,共24分)
11.将方程变形为用含x的代数式表示y的形式: .
12.若关于x的方程(2﹣a)x|a|﹣1﹣a=0是一元一次方程,则a= .
13.已知是关于的方程的解,则当时,代数式的值为 .
14.当y=________时,1-与的值相等.
15.对于两个非零有理数a,b,规定:a b=ab-(a+b).若2 (x+1)=1
则x的值为________.
16.一个两位数,十位上的数字比个位上的数字小1,十位与个位上的数字之
和是这个两位数的,则这个两位数是________.
17.甲有图书60册,乙有图书36册,若要使甲、乙两人的图书一样多,设甲应给乙图书本,则可列方程___________.
18.将一个棱长为的正方体铁块融化,铸造成高是的圆柱形铁块,圆柱形铁块的底面积是________.
三.解答题(共46分,19题6分,20 ---24题8分)
19.解下列方程:
(1); (2);
(3); (4).
20.当为何值时,关于的方程的解比关于的方程 的解大2?
21.当n为何值时,关于x的方程的解为0?
22. 已知,x=2是方程2﹣(m﹣x)=2x的解,求代数式m2﹣(6m+2)的值.
23.为鼓励节约用水,高港区自来水公司推行阶梯式水价计费制,标准如下表:
用水吨数 水费缴纳标准
每月用水不超过10吨 每吨a元收费
每月用水超过10吨 超过部分每吨2元收费
已知王奶奶家今年5月份用了8吨水,共缴纳水费12元.
(1)请求出a的值;
(2)若小明家今年8月份共缴纳水费37元,请求出8月份小明家的用水量.
24.某车间计划加工一批产品.如果每小时加工产品10个,就可以在预定时间完成任务;实际加工两个小时后,提高了加工速度,每小时多加工2个,结果提前1小时完成任务.
(1)该产品一共多少个?
(2)若该产品销售时按成本价提高40%后进行标价,按标价的8折销售时,每个产品仍可以获利15元,这批产品总成本为多少元?
参考答案
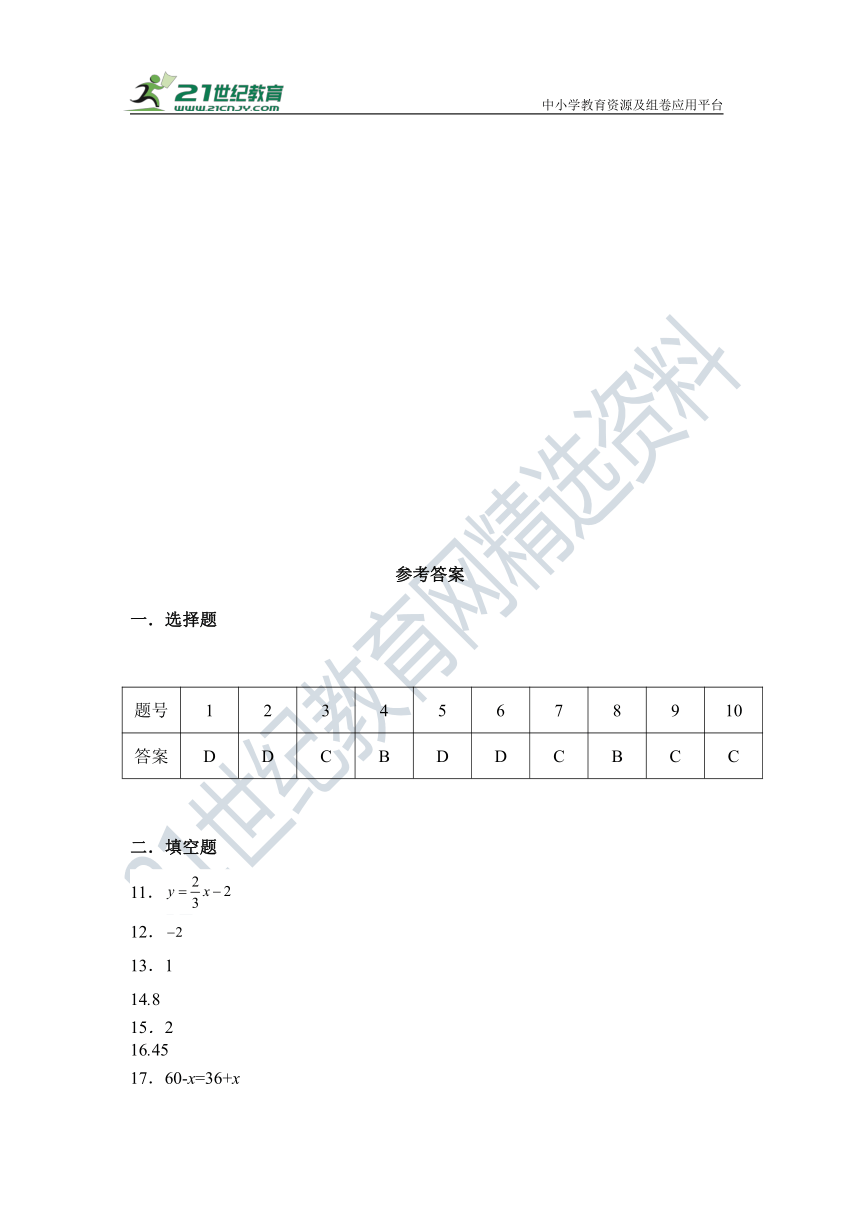
一.选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D D C B D D C B C C
二.填空题
11.
12.
13.1
14.8
15.2
16.45
17.60-x=36+x
18.32
三.解答题
19.解:(1),
去括号,得
移项,得,
系数化为1,得
(2) ,
去分母,得,
去括号,得,
移项,得,
合并同类项,得
系数化为1,得
(3),
去括号,得,
移项,得,
合并同类项,得,
系数化为1,得
(4),
去分母,得,
去括号,得,
移项,得,
合并同类项,得,
系数化为1,得
20.解:方程的解是, 方程的解是.
由题意可知,解关于m的方程得.
故当时,关于的方程的解比关于的方程的解大2.
21.解:把x=0代入方程得,
+1=+n,去分母得,
2n+6=3+6n,所以n=,
即当n= 时,关于x的方程的解为0.
22. 解:把x=2代入方程得:2﹣(m﹣2)=4,
解得:m=﹣4,
则m2﹣(6m+2)
=16﹣(﹣24+2)
=38.
23.解:(1)设2号线每千米的平均造价为x亿元,则3号线每千米的平均造价为(x+0.2)亿元,
依题意,得:32x+66(x+0.2)=581.6,
解得:x=5.8,
∴x+0.2=6.
答:2号线每千米的平均造价为5.8亿元,3号线每千米的平均造价为6亿元.
(2)6×1.2×182=1310.4(亿元).
答:还需投资1310.4亿元.
24.解:(1)∵点A表示的数为8,B在A点左边,AB=15,
∴点B表示的数是8﹣15=﹣7,
∵动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,
∴点P表示的数是8﹣6t.
(2)设点P运动x秒时,在点C处追上点Q,
则AC=6x,BC=3x,
∵AC﹣BC=AB,
∴6x﹣3x=15,
解得:x=5,
∴点P运动5秒时追上点Q.
(3)若点D是数轴上一点可分为三种情况:
①当点D在点B的左侧或与点B重合时x≤﹣5,
则有BD=|x+5|=﹣(x+5)=﹣x﹣5,AD=|x﹣7|=﹣(x﹣7)=7﹣x,
∵|x+6|+|x﹣8|≥0,
∴﹣x﹣5+7﹣x≥0,
∴x≤1,
∴当x=﹣5时|x+5|+|x﹣7|存在最小值12,
②当点D在AB之间时﹣5<x<7,BD=|x+5|=x+5,AD=|x﹣7|=﹣(x﹣7)=7﹣x,
∵|x+5|+|x﹣7|=x+5+7﹣x=12,
∴式子|x+5|+|x﹣7|=12.
③当点D在点A的右侧时x≥7,则BD=|x+5|=x+6,AD=|x﹣7|=x﹣7,
∵|x+5|+|x﹣7|=x+5+x﹣7=2x﹣2≥0,
∴x≥1,
∴当x=7时,|x+5|+|x﹣7|=12为最小值,
综上所述当﹣5≤x≤7时,|x+5|+|x﹣7|存在最小值12.
23.解:(1)根据题意,得8a=12.
解得a=1.5.
答:a的值是1.5.
(2)当用水量为10吨时,10×1.5=15(元).
因为15<37,所以小明家8月份的用水量一定超过10吨.
设8月份小明家的用水量为x吨.
根据题意,得10×1.5+2(x-10)=37.
解得x=21.
答:8月份小明家的用水量是21吨.
24.解: (1) 设该产品一共有x个.依题意,得-=1.解得x=80.
答:该产品一共有80个.
(2)设该批产品成本为a元/个.依题意,得
a (1+40%) ×80%=a+15.
解得a=125.125×80=10 000.
答:该批产品总成本为10 000元.
第三章《一元一次方程》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(共10小题,每题3分,满分30分)
1.下列运用等式的性质进行的变形,不正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.方程x﹣2=2﹣x的解是( )
A.x=1 B.x=﹣1 C.x=2 D.x=0
3.已知式子的值与互为倒数,那么x的值是( )
A.6 B. C. D.5
4.三个正整数的比是,它们的和是,那么这三个数中最大的数是( )
A.56 B.48 C.36 D.12
5.如果是关于的方程的解,则值为( )
A. B. C. D.
6.下列表述正确的是( )
A.由,得 B.由,得
C.由,得 D.由,得
7.若与互为相反数,则a的值为( )
A. B. C. D.
8.已知x=2是关于x的一元一次方程mx+2=0的解,则m的值为( )
A.﹣1 B.0 C.1 D.2
9.某项工作甲单独做需4天完成,乙单独做需6天完成,若甲先做了一天,然后甲、乙合作完成此项工作,若设甲一共做了天,所列方程为( )
A. B. C. D.
10.干墨鱼用水浸泡后,重量可增加210%,某加工单位准备为某饭店提供湿墨鱼,问需要多少干墨鱼做原料?用x表示所需干墨鱼的数,则下列方程正确的是( ).
A. B. C. D.
二、填空题(每题3分,共24分)
11.将方程变形为用含x的代数式表示y的形式: .
12.若关于x的方程(2﹣a)x|a|﹣1﹣a=0是一元一次方程,则a= .
13.已知是关于的方程的解,则当时,代数式的值为 .
14.当y=________时,1-与的值相等.
15.对于两个非零有理数a,b,规定:a b=ab-(a+b).若2 (x+1)=1
则x的值为________.
16.一个两位数,十位上的数字比个位上的数字小1,十位与个位上的数字之
和是这个两位数的,则这个两位数是________.
17.甲有图书60册,乙有图书36册,若要使甲、乙两人的图书一样多,设甲应给乙图书本,则可列方程___________.
18.将一个棱长为的正方体铁块融化,铸造成高是的圆柱形铁块,圆柱形铁块的底面积是________.
三.解答题(共46分,19题6分,20 ---24题8分)
19.解下列方程:
(1); (2);
(3); (4).
20.当为何值时,关于的方程的解比关于的方程 的解大2?
21.当n为何值时,关于x的方程的解为0?
22. 已知,x=2是方程2﹣(m﹣x)=2x的解,求代数式m2﹣(6m+2)的值.
23.为鼓励节约用水,高港区自来水公司推行阶梯式水价计费制,标准如下表:
用水吨数 水费缴纳标准
每月用水不超过10吨 每吨a元收费
每月用水超过10吨 超过部分每吨2元收费
已知王奶奶家今年5月份用了8吨水,共缴纳水费12元.
(1)请求出a的值;
(2)若小明家今年8月份共缴纳水费37元,请求出8月份小明家的用水量.
24.某车间计划加工一批产品.如果每小时加工产品10个,就可以在预定时间完成任务;实际加工两个小时后,提高了加工速度,每小时多加工2个,结果提前1小时完成任务.
(1)该产品一共多少个?
(2)若该产品销售时按成本价提高40%后进行标价,按标价的8折销售时,每个产品仍可以获利15元,这批产品总成本为多少元?
参考答案
一.选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D D C B D D C B C C
二.填空题
11.
12.
13.1
14.8
15.2
16.45
17.60-x=36+x
18.32
三.解答题
19.解:(1),
去括号,得
移项,得,
系数化为1,得
(2) ,
去分母,得,
去括号,得,
移项,得,
合并同类项,得
系数化为1,得
(3),
去括号,得,
移项,得,
合并同类项,得,
系数化为1,得
(4),
去分母,得,
去括号,得,
移项,得,
合并同类项,得,
系数化为1,得
20.解:方程的解是, 方程的解是.
由题意可知,解关于m的方程得.
故当时,关于的方程的解比关于的方程的解大2.
21.解:把x=0代入方程得,
+1=+n,去分母得,
2n+6=3+6n,所以n=,
即当n= 时,关于x的方程的解为0.
22. 解:把x=2代入方程得:2﹣(m﹣2)=4,
解得:m=﹣4,
则m2﹣(6m+2)
=16﹣(﹣24+2)
=38.
23.解:(1)设2号线每千米的平均造价为x亿元,则3号线每千米的平均造价为(x+0.2)亿元,
依题意,得:32x+66(x+0.2)=581.6,
解得:x=5.8,
∴x+0.2=6.
答:2号线每千米的平均造价为5.8亿元,3号线每千米的平均造价为6亿元.
(2)6×1.2×182=1310.4(亿元).
答:还需投资1310.4亿元.
24.解:(1)∵点A表示的数为8,B在A点左边,AB=15,
∴点B表示的数是8﹣15=﹣7,
∵动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,
∴点P表示的数是8﹣6t.
(2)设点P运动x秒时,在点C处追上点Q,
则AC=6x,BC=3x,
∵AC﹣BC=AB,
∴6x﹣3x=15,
解得:x=5,
∴点P运动5秒时追上点Q.
(3)若点D是数轴上一点可分为三种情况:
①当点D在点B的左侧或与点B重合时x≤﹣5,
则有BD=|x+5|=﹣(x+5)=﹣x﹣5,AD=|x﹣7|=﹣(x﹣7)=7﹣x,
∵|x+6|+|x﹣8|≥0,
∴﹣x﹣5+7﹣x≥0,
∴x≤1,
∴当x=﹣5时|x+5|+|x﹣7|存在最小值12,
②当点D在AB之间时﹣5<x<7,BD=|x+5|=x+5,AD=|x﹣7|=﹣(x﹣7)=7﹣x,
∵|x+5|+|x﹣7|=x+5+7﹣x=12,
∴式子|x+5|+|x﹣7|=12.
③当点D在点A的右侧时x≥7,则BD=|x+5|=x+6,AD=|x﹣7|=x﹣7,
∵|x+5|+|x﹣7|=x+5+x﹣7=2x﹣2≥0,
∴x≥1,
∴当x=7时,|x+5|+|x﹣7|=12为最小值,
综上所述当﹣5≤x≤7时,|x+5|+|x﹣7|存在最小值12.
23.解:(1)根据题意,得8a=12.
解得a=1.5.
答:a的值是1.5.
(2)当用水量为10吨时,10×1.5=15(元).
因为15<37,所以小明家8月份的用水量一定超过10吨.
设8月份小明家的用水量为x吨.
根据题意,得10×1.5+2(x-10)=37.
解得x=21.
答:8月份小明家的用水量是21吨.
24.解: (1) 设该产品一共有x个.依题意,得-=1.解得x=80.
答:该产品一共有80个.
(2)设该批产品成本为a元/个.依题意,得
a (1+40%) ×80%=a+15.
解得a=125.125×80=10 000.
答:该批产品总成本为10 000元.
