第14章 整式乘除与因式分解单元检测试题4(含答案)
文档属性
| 名称 | 第14章 整式乘除与因式分解单元检测试题4(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 205.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-11 19:15:05 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十四章《整式的乘法与因式分解》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.下列多项式,不能运用平方差公式分解的是( )
A.-m2+4 B.-x2-y2
C.x2y2-1 D.(m+n)2-(a+b)2
2.计算a ·a的结果是( )
A.a B. a C.a D. a
3.下列计算结果正确的是( )
A.(a b2)3=ab6 B.(-a3)2=a9
C.a2 a3=a6 D.(-a)6÷(-a)2=a4
4.下列因式分解正确的是( )
A.x2﹣4=(x+4)(x﹣4) B.x2+2x+1=x(x+2)+1
C.3mx﹣6my=3m(x﹣6y) D.x2y﹣y3=y(x+y)(x﹣y)
5.多项式可以因式分解成,则的值是( )
A.-1 B.1 C.-5 D.5
6.如果 ,那么用含m的代数式表示n为( )
A. B. C. D.
7.记 ,且 ,则 ( ).
A.128 B.32 C.64 D.16
8.若x2+mx+k是一个完全平方式,则k等于( )
A. B. C. D.m2
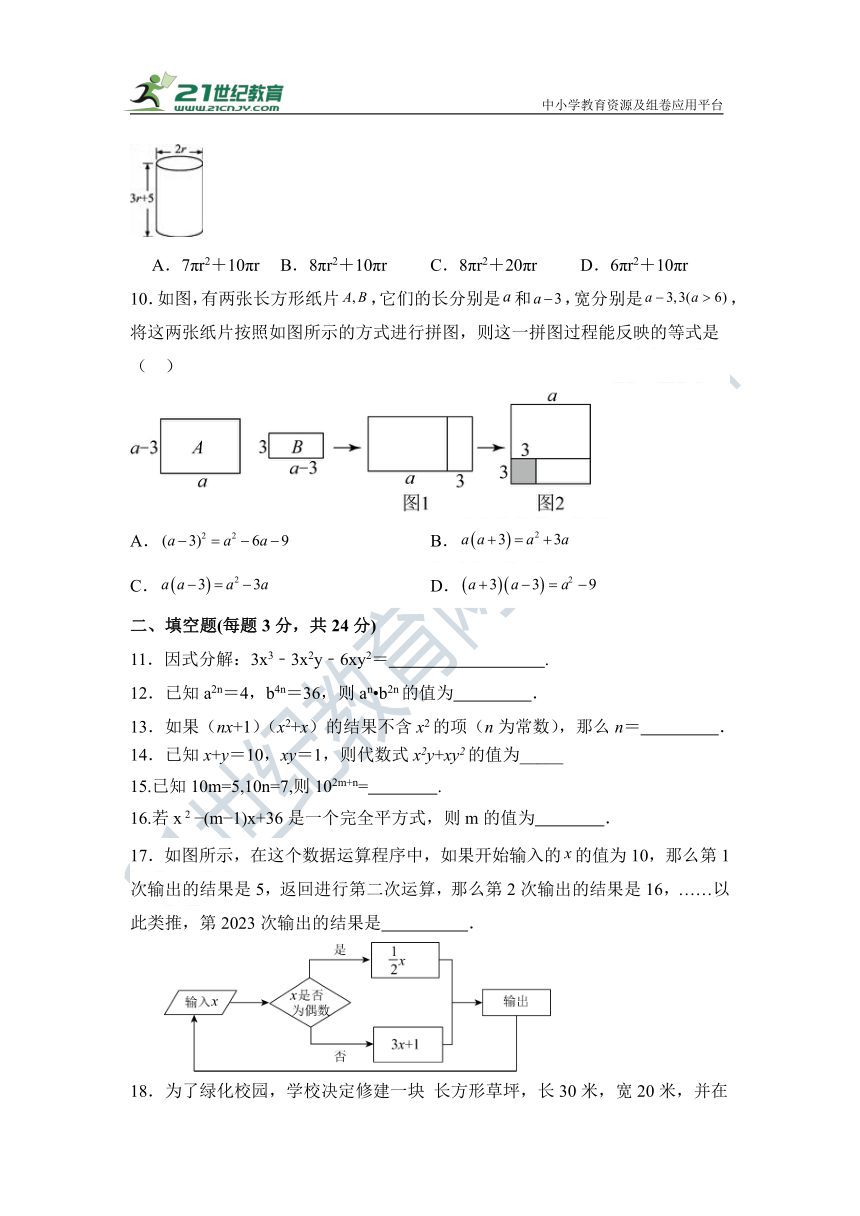
9.某圆柱体的底面直径和高如图所示,则这个圆柱体的表面积为( )
A.7πr2+10πr B.8πr2+10πr C.8πr2+20πr D.6πr2+10πr
10.如图,有两张长方形纸片,它们的长分别是和,宽分别是,将这两张纸片按照如图所示的方式进行拼图,则这一拼图过程能反映的等式是( )
A. B.
C. D.
二、填空题(每题3分,共24分)
11.因式分解:3x3﹣3x2y﹣6xy2= .
12.已知a2n=4,b4n=36,则an b2n的值为 .
13.如果(nx+1)(x2+x)的结果不含x2的项(n为常数),那么n= .
14.已知x+y=10,xy=1,则代数式x2y+xy2的值为_____
15.已知10m=5,10n=7,则102m+n= .
16.若x (m 1)x+36是一个完全平方式,则m的值为 .
17.如图所示,在这个数据运算程序中,如果开始输入的的值为10,那么第1次输出的结果是5,返回进行第二次运算,那么第2次输出的结果是16,……以此类推,第2023次输出的结果是 .
18.为了绿化校园,学校决定修建一块 长方形草坪,长30米,宽20米,并在草坪上修建如图所示的等宽的十字路,小路宽为x米,用代数式表示草坪的面积是 平方米(化成最简形式).
三.解答题(共46分,19题6分,20 ---24题8分)
19.计算:
(1)(-1)2 018+-(3.14-π)0; (2)(2x3y)2·(-2xy)+(-2x3y)3÷2x2;
(3)(2x-3)2-(2x+3)(2x-3); (4)[(a-2b)2+(a-2b)(2b+a)-2a(2a-b)]÷2a.
20.分解因式:
(1)m3n-9mn; (2)(x2+4)2-16x2;
(3)x2-4y2-x+2y; (4)4x3y+4x2y2+xy3.
21.先化简,再求值:
(1)(x2-4xy+4y2)÷(x-2y)-(4x2-9y2)÷(2x-3y),其中x=-4,y=;
(2)(m-n)(m+n)+(m+n)2-2m2,其中m,n满足
22.若a,b,c是△ABC的三边,满足a2(c2﹣a2)=b2(c2﹣b2),判断并说明△ABC的形状.
23.完全平方公式: 适当的变形,可以解决很多的数学问题.
例如:若 ,求 的值.
解:因为
所以
所以
得 .
根据上面的解题思路与方法,解决下列问题:
(1)若 ,求 的值;
(2)①若 ,则 ;
②若 则 ;
(3)如图,点C是线段 上的一点,以 为边向两边作正方形,设 ,两正方形的面积和 ,求图中阴影部分面积.
24.阅读与思考:分组分解法指通过分组分解的方式来分解用提公因式法和公式法无法直接分解的多项式,比如:四项的多项式一般按照“两两”分组或“三一”分组,进行分组分解.
例1:“两两分组”:
解:原式
例2:“三一分组”:
解:原式
归纳总结:用分组分解法分解因式要先恰当分组,然后用提公因式法或运用公式法继续分解.请同学们在阅读材料的启发下,解答下列问题:
(1)分解因式:
①;
②;
(2)已知的三边a,b,c满足,试判断的形状.
答案
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D D B B A A B D
二、填空题(每题3分,共24分)
11.3x(x+y)(x-2y)
12.±12
13.﹣1
14.10
15.175
16.若x (m 1)x+36是一个完全平方式,则m的值为 .
解析:∵x2 (m 1)x+36是一个完全平方式,
∴m 1=±12,
故m的值为 11或13,
故答案为: 11或13.
17.2,1
【解析】
∵|a﹣2|+b2﹣2b+1=0,
∴|a﹣2|+(b-1)2=0,
∴a-2=0,b-1=0,
∴a=2,b=1.
18.∵正方形的面积等于边长的平方,
∴正方形ABCD的面积为AB2,正方形AEFG的面积为AE2.
∴阴影部分的面积是AB2﹣AE2=(AB+AE)(AB﹣AE).
∵大正方形ABCD和小正方形AEFG的周长和为20,
∴AB+AE=20÷4=5.
∵阴影部分的面积是10,
∴(AB+AE)(AB﹣AE)=10.
∴AB﹣AE=2.
即BE=2.
故答案为2.
三.解答题(共46分,19题6分,20 ---24题8分)
19.解:(1)原式=1+-1=;
(2)原式=4x6y2·(-2xy)-8x9y3÷2x2=-8x7y3-4x7y3=-12x7y3;
(3)原式=(2x-3)·[(2x-3)-(2x+3)]=(2x-3)·(-6)=-12x+18;
(4)原式=(a2-4ab+4b2+a2-4b2-4a2+2ab)÷2a=(-2a2-2ab)÷2a=-a-b.
20.解:(1)原式=mn(m2-9)=mn(m+3)(m-3);
(2)原式=(x2+4+4x)(x2+4-4x)=(x+2)2(x-2)2;
(3)原式=x2-4y2-(x-2y)=(x+2y)(x-2y)-(x-2y)=(x-2y)(x+2y-1);
(4)原式=xy(4x2+4xy+y2)=xy(2x+y)2.
21.解:(1)原式=(x-2y)2÷(x-2y)-(2x+3y)(2x-3y)÷(2x-3y)=x-2y-2x-3y=-x-5y.
∵x=-4,y=,
∴原式=-x-5y=4-5×=3.
(2)原式=m2-n2+m2+2mn+n2-2m2=2mn.
解方程组
得
∴原式=2mn=2×3×(-1)=-6.
22.解:∵a2(c2﹣a2)=b2(c2﹣b2),
∴a2(c2﹣a2)﹣b2(c2﹣b2)=0
a2c2﹣a4﹣b2c2+b4=0
c2(a2﹣b2)﹣(a4﹣b4)=0
c2(a2﹣b2)﹣(a2+b2)(a2﹣b2)=0
(a2﹣b2)(c2﹣a2﹣b2)=0,
∴a2﹣b2=0或c2﹣a2﹣b2=0,
∵a,b,c是△ABC的三边,
∴a=b或c2=a2+b2,
∴△ABC是等腰三角形或直角三角形.
23.(1)解: ;
;
;
又 ;
,
,
∴ .
(2)6;17
(3)解:由题意可得, , ;
, ;
,
;
图中阴影部分面积为直角三角形面积,
,
.
24.(1)解:①x2-xy+5x-5y
=(x2-xy)+(5x-5y)
=x(x-y)+5(x-y)
=(x-y)(x+5);
②m2-n2-6m+9
=(m2-6m+9)-n2
=(m-3)2-n2
=(m-3+n)(m-3-n);
(2)解:∵a2-b2-ac+bc=0,
∴(a2-b2)-(ac-bc)=0,
∴(a+b)(a-b)-c(a-b)=0,
∴(a-b)(a+b-c)=0,
∵a,b,c是△ABC的三边,
∴a+b-c>0,
∴a-b=0,
∴a=b,
即△ABC是等腰三角形
第十四章《整式的乘法与因式分解》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.下列多项式,不能运用平方差公式分解的是( )
A.-m2+4 B.-x2-y2
C.x2y2-1 D.(m+n)2-(a+b)2
2.计算a ·a的结果是( )
A.a B. a C.a D. a
3.下列计算结果正确的是( )
A.(a b2)3=ab6 B.(-a3)2=a9
C.a2 a3=a6 D.(-a)6÷(-a)2=a4
4.下列因式分解正确的是( )
A.x2﹣4=(x+4)(x﹣4) B.x2+2x+1=x(x+2)+1
C.3mx﹣6my=3m(x﹣6y) D.x2y﹣y3=y(x+y)(x﹣y)
5.多项式可以因式分解成,则的值是( )
A.-1 B.1 C.-5 D.5
6.如果 ,那么用含m的代数式表示n为( )
A. B. C. D.
7.记 ,且 ,则 ( ).
A.128 B.32 C.64 D.16
8.若x2+mx+k是一个完全平方式,则k等于( )
A. B. C. D.m2
9.某圆柱体的底面直径和高如图所示,则这个圆柱体的表面积为( )
A.7πr2+10πr B.8πr2+10πr C.8πr2+20πr D.6πr2+10πr
10.如图,有两张长方形纸片,它们的长分别是和,宽分别是,将这两张纸片按照如图所示的方式进行拼图,则这一拼图过程能反映的等式是( )
A. B.
C. D.
二、填空题(每题3分,共24分)
11.因式分解:3x3﹣3x2y﹣6xy2= .
12.已知a2n=4,b4n=36,则an b2n的值为 .
13.如果(nx+1)(x2+x)的结果不含x2的项(n为常数),那么n= .
14.已知x+y=10,xy=1,则代数式x2y+xy2的值为_____
15.已知10m=5,10n=7,则102m+n= .
16.若x (m 1)x+36是一个完全平方式,则m的值为 .
17.如图所示,在这个数据运算程序中,如果开始输入的的值为10,那么第1次输出的结果是5,返回进行第二次运算,那么第2次输出的结果是16,……以此类推,第2023次输出的结果是 .
18.为了绿化校园,学校决定修建一块 长方形草坪,长30米,宽20米,并在草坪上修建如图所示的等宽的十字路,小路宽为x米,用代数式表示草坪的面积是 平方米(化成最简形式).
三.解答题(共46分,19题6分,20 ---24题8分)
19.计算:
(1)(-1)2 018+-(3.14-π)0; (2)(2x3y)2·(-2xy)+(-2x3y)3÷2x2;
(3)(2x-3)2-(2x+3)(2x-3); (4)[(a-2b)2+(a-2b)(2b+a)-2a(2a-b)]÷2a.
20.分解因式:
(1)m3n-9mn; (2)(x2+4)2-16x2;
(3)x2-4y2-x+2y; (4)4x3y+4x2y2+xy3.
21.先化简,再求值:
(1)(x2-4xy+4y2)÷(x-2y)-(4x2-9y2)÷(2x-3y),其中x=-4,y=;
(2)(m-n)(m+n)+(m+n)2-2m2,其中m,n满足
22.若a,b,c是△ABC的三边,满足a2(c2﹣a2)=b2(c2﹣b2),判断并说明△ABC的形状.
23.完全平方公式: 适当的变形,可以解决很多的数学问题.
例如:若 ,求 的值.
解:因为
所以
所以
得 .
根据上面的解题思路与方法,解决下列问题:
(1)若 ,求 的值;
(2)①若 ,则 ;
②若 则 ;
(3)如图,点C是线段 上的一点,以 为边向两边作正方形,设 ,两正方形的面积和 ,求图中阴影部分面积.
24.阅读与思考:分组分解法指通过分组分解的方式来分解用提公因式法和公式法无法直接分解的多项式,比如:四项的多项式一般按照“两两”分组或“三一”分组,进行分组分解.
例1:“两两分组”:
解:原式
例2:“三一分组”:
解:原式
归纳总结:用分组分解法分解因式要先恰当分组,然后用提公因式法或运用公式法继续分解.请同学们在阅读材料的启发下,解答下列问题:
(1)分解因式:
①;
②;
(2)已知的三边a,b,c满足,试判断的形状.
答案
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D D B B A A B D
二、填空题(每题3分,共24分)
11.3x(x+y)(x-2y)
12.±12
13.﹣1
14.10
15.175
16.若x (m 1)x+36是一个完全平方式,则m的值为 .
解析:∵x2 (m 1)x+36是一个完全平方式,
∴m 1=±12,
故m的值为 11或13,
故答案为: 11或13.
17.2,1
【解析】
∵|a﹣2|+b2﹣2b+1=0,
∴|a﹣2|+(b-1)2=0,
∴a-2=0,b-1=0,
∴a=2,b=1.
18.∵正方形的面积等于边长的平方,
∴正方形ABCD的面积为AB2,正方形AEFG的面积为AE2.
∴阴影部分的面积是AB2﹣AE2=(AB+AE)(AB﹣AE).
∵大正方形ABCD和小正方形AEFG的周长和为20,
∴AB+AE=20÷4=5.
∵阴影部分的面积是10,
∴(AB+AE)(AB﹣AE)=10.
∴AB﹣AE=2.
即BE=2.
故答案为2.
三.解答题(共46分,19题6分,20 ---24题8分)
19.解:(1)原式=1+-1=;
(2)原式=4x6y2·(-2xy)-8x9y3÷2x2=-8x7y3-4x7y3=-12x7y3;
(3)原式=(2x-3)·[(2x-3)-(2x+3)]=(2x-3)·(-6)=-12x+18;
(4)原式=(a2-4ab+4b2+a2-4b2-4a2+2ab)÷2a=(-2a2-2ab)÷2a=-a-b.
20.解:(1)原式=mn(m2-9)=mn(m+3)(m-3);
(2)原式=(x2+4+4x)(x2+4-4x)=(x+2)2(x-2)2;
(3)原式=x2-4y2-(x-2y)=(x+2y)(x-2y)-(x-2y)=(x-2y)(x+2y-1);
(4)原式=xy(4x2+4xy+y2)=xy(2x+y)2.
21.解:(1)原式=(x-2y)2÷(x-2y)-(2x+3y)(2x-3y)÷(2x-3y)=x-2y-2x-3y=-x-5y.
∵x=-4,y=,
∴原式=-x-5y=4-5×=3.
(2)原式=m2-n2+m2+2mn+n2-2m2=2mn.
解方程组
得
∴原式=2mn=2×3×(-1)=-6.
22.解:∵a2(c2﹣a2)=b2(c2﹣b2),
∴a2(c2﹣a2)﹣b2(c2﹣b2)=0
a2c2﹣a4﹣b2c2+b4=0
c2(a2﹣b2)﹣(a4﹣b4)=0
c2(a2﹣b2)﹣(a2+b2)(a2﹣b2)=0
(a2﹣b2)(c2﹣a2﹣b2)=0,
∴a2﹣b2=0或c2﹣a2﹣b2=0,
∵a,b,c是△ABC的三边,
∴a=b或c2=a2+b2,
∴△ABC是等腰三角形或直角三角形.
23.(1)解: ;
;
;
又 ;
,
,
∴ .
(2)6;17
(3)解:由题意可得, , ;
, ;
,
;
图中阴影部分面积为直角三角形面积,
,
.
24.(1)解:①x2-xy+5x-5y
=(x2-xy)+(5x-5y)
=x(x-y)+5(x-y)
=(x-y)(x+5);
②m2-n2-6m+9
=(m2-6m+9)-n2
=(m-3)2-n2
=(m-3+n)(m-3-n);
(2)解:∵a2-b2-ac+bc=0,
∴(a2-b2)-(ac-bc)=0,
∴(a+b)(a-b)-c(a-b)=0,
∴(a-b)(a+b-c)=0,
∵a,b,c是△ABC的三边,
∴a+b-c>0,
∴a-b=0,
∴a=b,
即△ABC是等腰三角形
