第24章 圆单元检测试题2(含答案)
文档属性
| 名称 | 第24章 圆单元检测试题2(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 313.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-11 19:21:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二十四章《圆》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1. 如图, 是 的外接圆,,则 的度数等于
A. B. C. D.
2. 如图,已知在 中, 是弦,半径 ,垂足为点 ,要使四边形 为菱形,还需要添加一个条件,这个条件可以是
A. B.
C. D.
3. 已知 的半径为 ,如果圆心 到直线 的距离为 ,那么
直线 与 的位置关系是
A.相交 B.相切 C.相离 D.不确定
4.如图,⊙O的直径CD垂直弦AB于点E,且CE=2,DE=8,则BE的长为( )
A.2 B.4 C.6 D.8
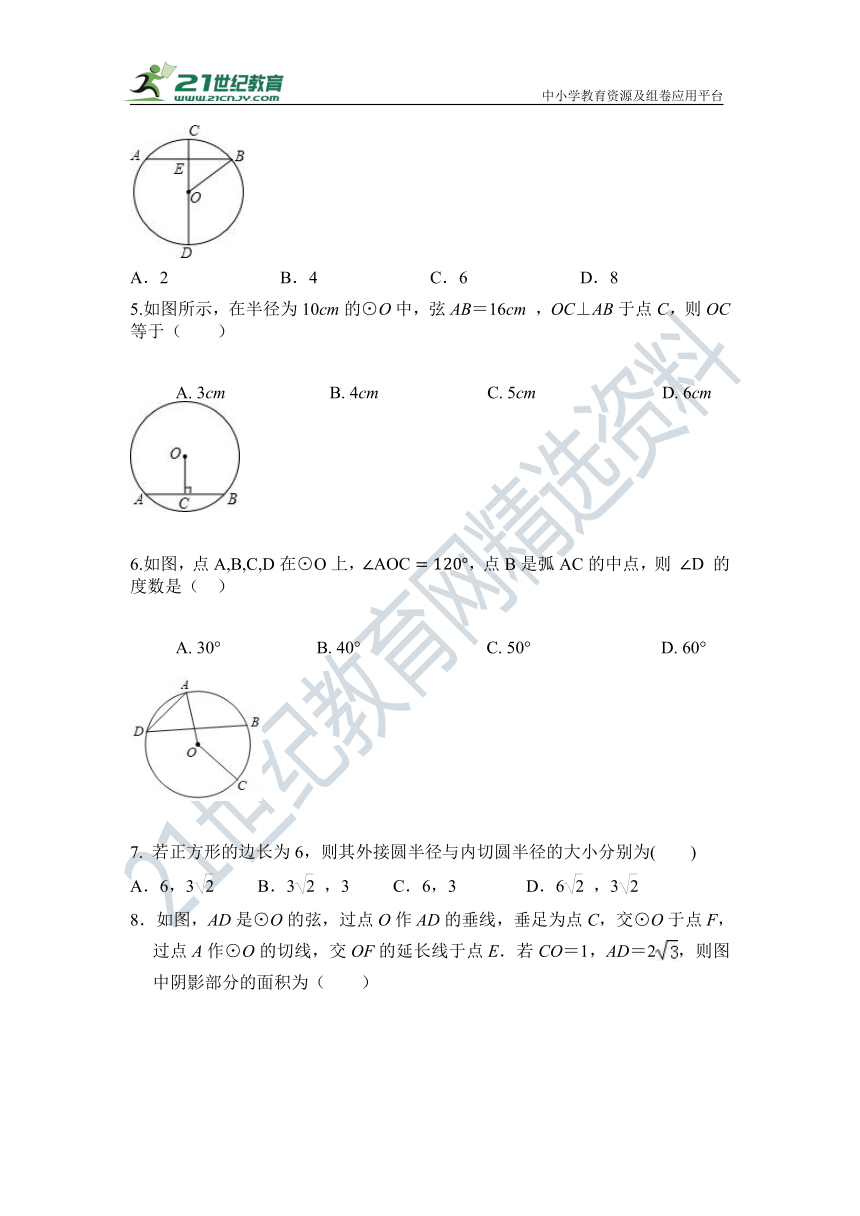
5.如图所示,在半径为10cm的⊙O中,弦AB=16cm ,OC⊥AB于点C,则OC等于( )
A. 3cm B. 4cm C. 5cm D. 6cm
6.如图,点A,B,C,D在⊙O上,,点B是弧AC的中点,则 的度数是( )
A. 30° B. 40° C. 50° D. 60°
7. 若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
A.6,3 B.3,3 C.6,3 D.6,3
8.如图,AD是⊙O的弦,过点O作AD的垂线,垂足为点C,交⊙O于点F,过点A作⊙O的切线,交OF的延长线于点E.若CO=1,AD=2,则图中阴影部分的面积为( )
A.4﹣π B.2﹣π C.4﹣π D.2﹣π
9.如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
A. B.2 C. D.
10.如图,3个正方形在⊙O直径的同侧,顶点B,C,G,H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上,顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则正方形PCGQ的面积为( )
A.5 B.6 C.7 D.10
二、填空题(每题3分,共24分)
11.如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD= .
12.如图,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB为0.8m,则排水管内水的深度为______m.
13. 如图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AB的延长线于点D.若∠A=32°,则∠D=_____度.
14.线段AD过圆心O,交⊙O于点C、D.∠A=24°,AE交⊙O于点B,且CD=2AB,则∠EOD= .
15.如图,在半径为的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=4,则OP的长为 .
16. 如图,, 是 上的两点, 是 上不与 , 重合的任意一点.如果 ,那么 的度数为 .
17. 在 中,,,,如果以点 为圆心, 为半径,且 与斜边 仅有一个公共点,那么半径 的取值范围是 .
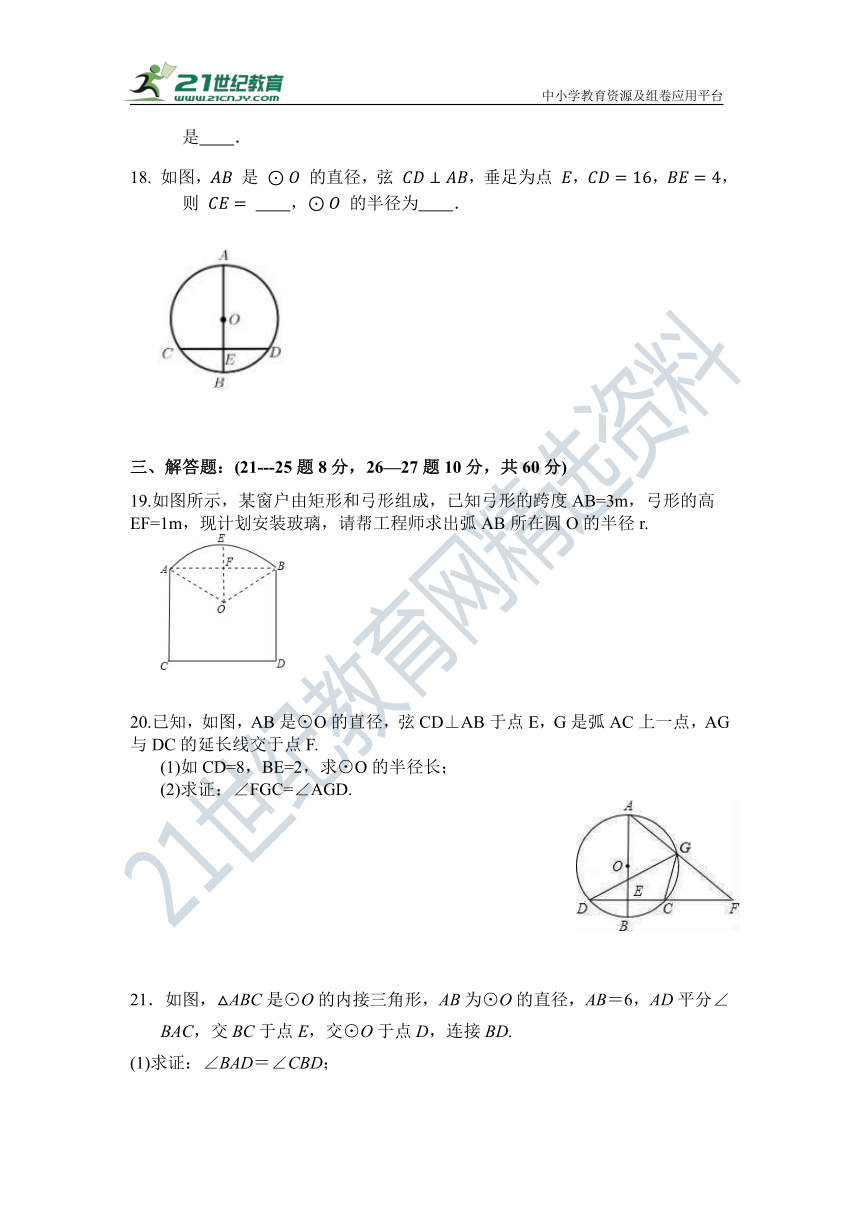
18. 如图, 是 的直径,弦 ,垂足为点 ,,,则 , 的半径为 .
三、解答题:(21---25题8分,26—27题10分,共60分)
19.如图所示,某窗户由矩形和弓形组成,已知弓形的跨度AB=3m,弓形的高EF=1m,现计划安装玻璃,请帮工程师求出弧AB所在圆O的半径r.
20.已知,如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上一点,AG与DC的延长线交于点F.
(1)如CD=8,BE=2,求⊙O的半径长;
(2)求证:∠FGC=∠AGD.
21.如图,△ABC是⊙O的内接三角形,AB为⊙O的直径,AB=6,AD平分∠BAC,交BC于点E,交⊙O于点D,连接BD.
(1)求证:∠BAD=∠CBD;
(2)若∠AEB=125°,求的长(结果保留π).
22.已知PA,PB分别与⊙O相切于点A,B,∠APB=80°,C为优弧AB上一点.
(1)如图①,求∠ACB的大小;
(2)如图②,AE为⊙O的直径,AE与BC相交于点D.若AB=AD,求∠EAC的大小.
23.如图,点E为⊙O的直径AB上一个动点,点C、D在下半圆AB上(不含A、B两点),
且∠CED=∠OED=60°,连OC、OD
(1)求证:∠C=∠D;
(2)若⊙O的半径为r,请直接写出CE+ED的变化范围.
24.以原点O为圆心,1cm为半径的圆分别交x、y轴的正半轴于A、B两点,点P的坐标为(2,0),动点Q从点B处出发,沿圆周按顺时针方向匀速运动一周,设运动的时间为秒.
(1)如图一,当t=1时,直线PQ恰好与⊙O第一次相切,连接OQ.求此时点Q的运动速度(结果保留π);
(2)若点Q按照(1)中的速度继续运动.
①当为何值时,以O、P、Q为顶点的三角形是直角三角形;
②在①的条件下,如果直线PQ与⊙O相交,请求出直线PQ被⊙O所截的弦长.
参考答案
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B A B D B D C C B
二、填空题(每题3分,共24分)
11.60
12.215
13.15°或75°
14. 72°.
15..
16. 【答案】 或
17. 【答案】 或
18. 【答案】 ;
三.解答题(共46分,19题6分,20 ---24题8分)
解:
(1)解:连接OC.设⊙O的半径为R.
∵CD⊥AB,
∴DE=EC=4,
在Rt△OEC中,∵OC2=OE2+EC2,
∴R2=(R﹣2)2+42,解得R=5.
(2)证明:连接AD,
∵弦CD⊥AB
∴=,
∴∠ADC=∠AGD,
∵四边形ADCG是圆内接四边形,
∴∠ADC=∠FGC,
∴∠FGC=∠AGD.
21.(1)证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.
又∵∠CBD=∠CAD,
∴∠BAD=∠CBD.
(2)解:连接OD.
∵∠AEB=125°,∴∠AEC=55°.
∵AB为⊙O的直径,
∴∠ACE=90°.
∴∠CAE=35°.
∴∠DAB=35°.
则所对圆心角∠DOB=70°.
∴的长为=π.
22.解:(1)连接OA,OB.
∵PA,PB是⊙O的切线,
∴∠OAP=∠OBP=90°.
∴∠AOB=360°-90°-90°-80°=100°.
∴∠ACB=∠AOB=50°.
(2)连接CE.
∵AE为⊙O的直径,∴∠ACE=90°.
∵∠ACB=50°,
∴∠BCE=90°-50°=40°.
∴∠BAE=∠BCE=40°.
∵AB=AD,∴∠ABD=∠ADB=70°.
∴∠EAC=∠ADB-∠ACB=20°.
23.证明:(1)延长CE交⊙O于D′,连接OD′
∵∠CED=∠OED=60°,
∴∠AEC=60°,
∴∠OED′=60°,
∴∠DEO=∠D′EO=60°,
由轴对称的性质可得∠D=∠D′,ED=ED′,
∵OC=OD′,
∴∠D′=∠C,
∴∠C=∠D;
(2)∵∠D′EO=60°,
∴∠C<60°,
∴∠C=∠D′<60°,
∴∠COD′>60°,
∴CD′>OC=OD′,
∵CD′<OC+OD′,
∵CE+ED=CE+ED′=CD′,
∴r<CE+ED<2r.
24.解:
(1)连接OQ,则OQ⊥PQ,OQ=1,OP=2,
所以°,即 °,
,
所以点Q的运动速度为/秒.
(2) ①由(1)可知,当t=1时,△OPQ为直角三角形,
所以,当Q'与Q关于x轴对称时,△OPQ'为直角三角形,
此时°,,,
当Q'(0,-1)或Q'(0,1)时,°,
此时t=6或,
即当t=5,t=6或t=12时,△OPQ是直角三角形.
②当t=6或t=12时,直线PQ与⊙O相交.作OM⊥PQ,
根据等面积法可知:PQ×OM=OQ×OP,PQ=, ,
,
弦长.
第二十四章《圆》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1. 如图, 是 的外接圆,,则 的度数等于
A. B. C. D.
2. 如图,已知在 中, 是弦,半径 ,垂足为点 ,要使四边形 为菱形,还需要添加一个条件,这个条件可以是
A. B.
C. D.
3. 已知 的半径为 ,如果圆心 到直线 的距离为 ,那么
直线 与 的位置关系是
A.相交 B.相切 C.相离 D.不确定
4.如图,⊙O的直径CD垂直弦AB于点E,且CE=2,DE=8,则BE的长为( )
A.2 B.4 C.6 D.8
5.如图所示,在半径为10cm的⊙O中,弦AB=16cm ,OC⊥AB于点C,则OC等于( )
A. 3cm B. 4cm C. 5cm D. 6cm
6.如图,点A,B,C,D在⊙O上,,点B是弧AC的中点,则 的度数是( )
A. 30° B. 40° C. 50° D. 60°
7. 若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
A.6,3 B.3,3 C.6,3 D.6,3
8.如图,AD是⊙O的弦,过点O作AD的垂线,垂足为点C,交⊙O于点F,过点A作⊙O的切线,交OF的延长线于点E.若CO=1,AD=2,则图中阴影部分的面积为( )
A.4﹣π B.2﹣π C.4﹣π D.2﹣π
9.如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
A. B.2 C. D.
10.如图,3个正方形在⊙O直径的同侧,顶点B,C,G,H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上,顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则正方形PCGQ的面积为( )
A.5 B.6 C.7 D.10
二、填空题(每题3分,共24分)
11.如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD= .
12.如图,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB为0.8m,则排水管内水的深度为______m.
13. 如图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AB的延长线于点D.若∠A=32°,则∠D=_____度.
14.线段AD过圆心O,交⊙O于点C、D.∠A=24°,AE交⊙O于点B,且CD=2AB,则∠EOD= .
15.如图,在半径为的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=4,则OP的长为 .
16. 如图,, 是 上的两点, 是 上不与 , 重合的任意一点.如果 ,那么 的度数为 .
17. 在 中,,,,如果以点 为圆心, 为半径,且 与斜边 仅有一个公共点,那么半径 的取值范围是 .
18. 如图, 是 的直径,弦 ,垂足为点 ,,,则 , 的半径为 .
三、解答题:(21---25题8分,26—27题10分,共60分)
19.如图所示,某窗户由矩形和弓形组成,已知弓形的跨度AB=3m,弓形的高EF=1m,现计划安装玻璃,请帮工程师求出弧AB所在圆O的半径r.
20.已知,如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上一点,AG与DC的延长线交于点F.
(1)如CD=8,BE=2,求⊙O的半径长;
(2)求证:∠FGC=∠AGD.
21.如图,△ABC是⊙O的内接三角形,AB为⊙O的直径,AB=6,AD平分∠BAC,交BC于点E,交⊙O于点D,连接BD.
(1)求证:∠BAD=∠CBD;
(2)若∠AEB=125°,求的长(结果保留π).
22.已知PA,PB分别与⊙O相切于点A,B,∠APB=80°,C为优弧AB上一点.
(1)如图①,求∠ACB的大小;
(2)如图②,AE为⊙O的直径,AE与BC相交于点D.若AB=AD,求∠EAC的大小.
23.如图,点E为⊙O的直径AB上一个动点,点C、D在下半圆AB上(不含A、B两点),
且∠CED=∠OED=60°,连OC、OD
(1)求证:∠C=∠D;
(2)若⊙O的半径为r,请直接写出CE+ED的变化范围.
24.以原点O为圆心,1cm为半径的圆分别交x、y轴的正半轴于A、B两点,点P的坐标为(2,0),动点Q从点B处出发,沿圆周按顺时针方向匀速运动一周,设运动的时间为秒.
(1)如图一,当t=1时,直线PQ恰好与⊙O第一次相切,连接OQ.求此时点Q的运动速度(结果保留π);
(2)若点Q按照(1)中的速度继续运动.
①当为何值时,以O、P、Q为顶点的三角形是直角三角形;
②在①的条件下,如果直线PQ与⊙O相交,请求出直线PQ被⊙O所截的弦长.
参考答案
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B A B D B D C C B
二、填空题(每题3分,共24分)
11.60
12.215
13.15°或75°
14. 72°.
15..
16. 【答案】 或
17. 【答案】 或
18. 【答案】 ;
三.解答题(共46分,19题6分,20 ---24题8分)
解:
(1)解:连接OC.设⊙O的半径为R.
∵CD⊥AB,
∴DE=EC=4,
在Rt△OEC中,∵OC2=OE2+EC2,
∴R2=(R﹣2)2+42,解得R=5.
(2)证明:连接AD,
∵弦CD⊥AB
∴=,
∴∠ADC=∠AGD,
∵四边形ADCG是圆内接四边形,
∴∠ADC=∠FGC,
∴∠FGC=∠AGD.
21.(1)证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.
又∵∠CBD=∠CAD,
∴∠BAD=∠CBD.
(2)解:连接OD.
∵∠AEB=125°,∴∠AEC=55°.
∵AB为⊙O的直径,
∴∠ACE=90°.
∴∠CAE=35°.
∴∠DAB=35°.
则所对圆心角∠DOB=70°.
∴的长为=π.
22.解:(1)连接OA,OB.
∵PA,PB是⊙O的切线,
∴∠OAP=∠OBP=90°.
∴∠AOB=360°-90°-90°-80°=100°.
∴∠ACB=∠AOB=50°.
(2)连接CE.
∵AE为⊙O的直径,∴∠ACE=90°.
∵∠ACB=50°,
∴∠BCE=90°-50°=40°.
∴∠BAE=∠BCE=40°.
∵AB=AD,∴∠ABD=∠ADB=70°.
∴∠EAC=∠ADB-∠ACB=20°.
23.证明:(1)延长CE交⊙O于D′,连接OD′
∵∠CED=∠OED=60°,
∴∠AEC=60°,
∴∠OED′=60°,
∴∠DEO=∠D′EO=60°,
由轴对称的性质可得∠D=∠D′,ED=ED′,
∵OC=OD′,
∴∠D′=∠C,
∴∠C=∠D;
(2)∵∠D′EO=60°,
∴∠C<60°,
∴∠C=∠D′<60°,
∴∠COD′>60°,
∴CD′>OC=OD′,
∵CD′<OC+OD′,
∵CE+ED=CE+ED′=CD′,
∴r<CE+ED<2r.
24.解:
(1)连接OQ,则OQ⊥PQ,OQ=1,OP=2,
所以°,即 °,
,
所以点Q的运动速度为/秒.
(2) ①由(1)可知,当t=1时,△OPQ为直角三角形,
所以,当Q'与Q关于x轴对称时,△OPQ'为直角三角形,
此时°,,,
当Q'(0,-1)或Q'(0,1)时,°,
此时t=6或,
即当t=5,t=6或t=12时,△OPQ是直角三角形.
②当t=6或t=12时,直线PQ与⊙O相交.作OM⊥PQ,
根据等面积法可知:PQ×OM=OQ×OP,PQ=, ,
,
弦长.
同课章节目录
