数学人教A版(2019)必修第一册5.1.1任意角(共22张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.1.1任意角(共22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-11 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
高一数学必修1 第五章 三角函数
第1节 任意角
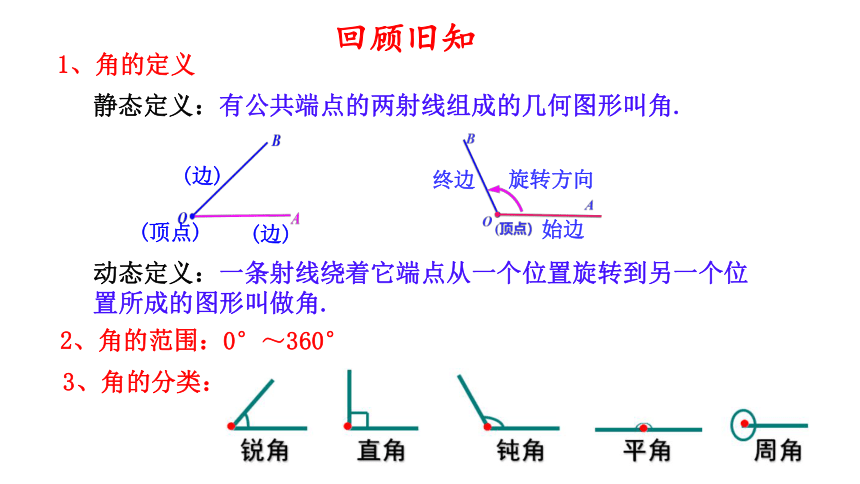
回顾旧知
静态定义:有公共端点的两射线组成的几何图形叫角.
(顶点)
(边)
(边)
动态定义:一条射线绕着它端点从一个位置旋转到另一个位置所成的图形叫做角.
始边
终边
旋转方向
1、角的定义
2、角的范围:
0°~360°
3、角的分类:
思考:角的范围可以超过吗?现实生活中有这样的例子吗?
“前空翻转体 540 度”
“后空翻转体 720 度”
OA绕点O旋转所成的角与O'B 绕点O'旋转所成的角就会有不同的方向.
钟表慢了 2 小时,校准后分针转过的角度
旋转度数+旋转方向
任意角的概念
平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形叫做角
始边:射线的起始位置;终边:射线的终止位置.
正角:一条射线绕其端点按逆时针方向旋转形成的角;
负角:一条射线绕其端点按顺时针方向旋转形成的角;
零角:一条射线没有做任何旋转,称它形成了一个零角。零角的始边与终边重合,如果零角,那么=0°.
旋转方向定符号,旋转量定大小(绝对值)
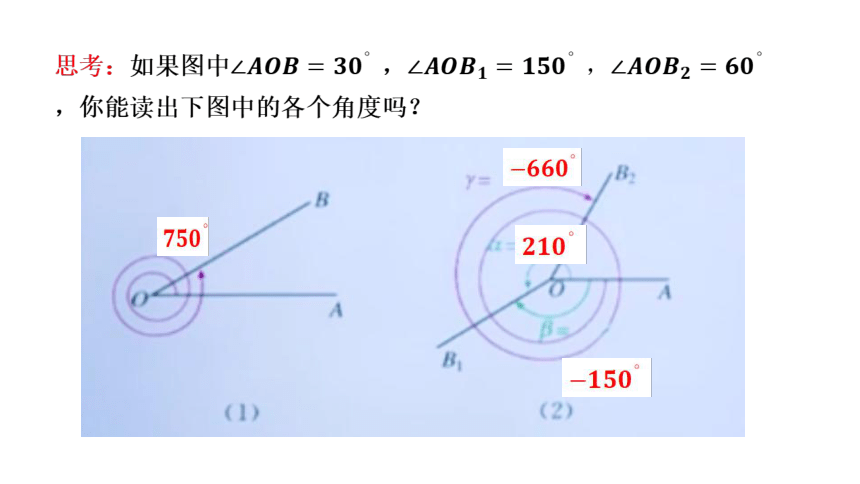
思考:如果图中,,你能读出下图中的各个角度吗?
在形成角的过程中,如果射线的旋转方向相同,且旋转量相等,则称这两个角相等。
若α与β相等,记为α=β。
设α,β 是任意两个角,规定:
α
β
α
α+β
β
加法:
把角α的终边旋转角β,这时终边所对应的角是α+β
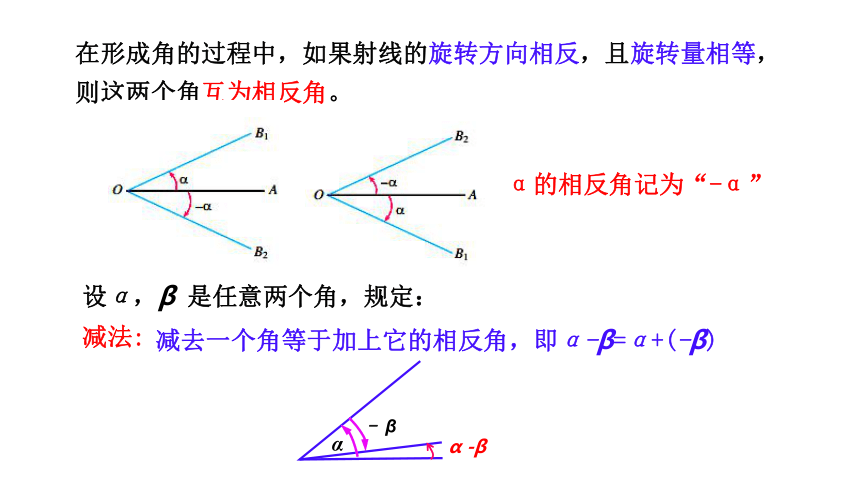
在形成角的过程中,如果射线的旋转方向相反,且旋转量相等,则这两个角互为相反角。
α的相反角记为“-α”
设α,β 是任意两个角,规定:
减去一个角等于加上它的相反角,即α-β=α+(-β)
α
- β
α -β
减法:
练习: 若90 <α<β<135 ,
则α-β的范围是_______________,
α+β的范围是________________.
(-45 , 0 )
(180 , 270 )
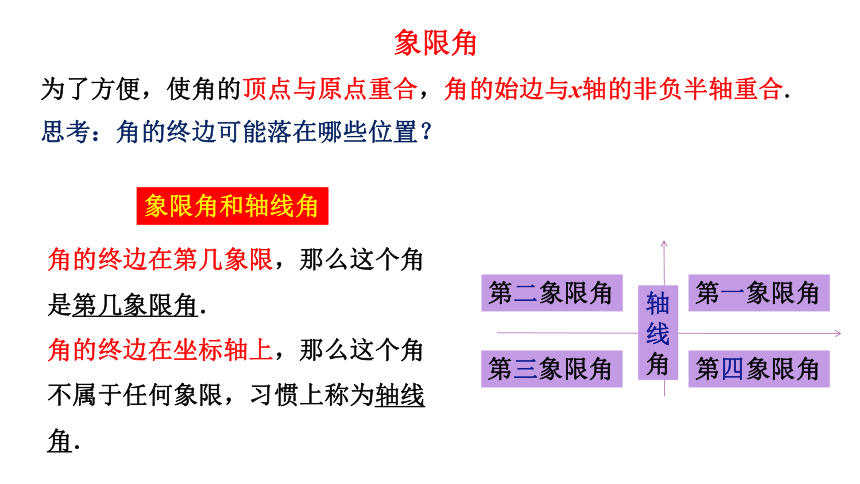
为了方便,使角的顶点与原点重合,角的始边与x轴的非负半轴重合.
思考:角的终边可能落在哪些位置?
象限角
第一象限角
第二象限角
第三象限角
第四象限角
轴线角
角的终边在第几象限,那么这个角是第几象限角.
角的终边在坐标轴上,那么这个角不属于任何象限,习惯上称为轴线角.
象限角和轴线角
练习:-50°,405°,210°,-200°,-450°分别是第几象限角?是正角还是负角?
课本P171页练习1.锐角是第几象限角 第一象限角一定是锐角吗 再分别就直角、钝角来回答这两个问题。
课本P171页练习3.已知角的顶点与原点重合, 角的始边与x轴的非负半轴重合, 请作出下列各角,并指出它们各是哪个象限的角?
(1)420 , (2)-75 , (3)855 , (4) -510 .
第一象限角
420
-75
第四象限角
855
第二象限角
-510
第三象限角
解:
在直角坐标系中作出下列各角:
对于直角坐标系内的任意一条射线,以它为终边的角并不唯一。
思考:能不能用集合的形式将它们表达出来?
还有没有与-32°终边相同的角?
与-32°终边相同的角有无数多个,它们与-32°角均相差360°的整数倍,都可以表示成-32°的角与k(k∈Z)个周角的和.
因此与-32°终边相同的所有角可以表示为
β= -32°+k 360°,k∈Z.
一般地,我们有:
所有与角 终边相同的角,连同角 在内,可构成一个集合
S ={β|β= +k·360°, },
即任一与角 终边相同的角,都可以表示成角 与整数个周角的和.
注意:(1) k∈Z。
“k >0”表示β是将α的终边逆时针旋转得到的;
“k <0”表示β是将α的终边顺时针旋转得到的;
“k =0”表示β就是α本身。
(2)α是任意角;
(3)终边相同的角不一定相相等,它们有无数多个,它们
之间差相差360 的整数倍
例2:写出终边在y轴上的角的集合
例3 写出终边在直线y=x上的角的集合S,S中满足不等式
-360°≤ β <720°的元素β有哪些?
解 S={β|β=45 +k·180 ,k∈Z}.
S中适合不等式-360 ≤ β< 720 的元素有:
-315 ,-135 , 45 , 225 , 405 , 585 .
小结
课本P171页练习2. 今天是星期三, 则7k(k∈Z)天后的那一天是星期几 7k(k∈Z)天前的那一天是星期几 100天后的那一天是星期几
7k(k∈Z)天后和7k天前的那一天都是星期三
∵100=14×7+2
∴100天后的那一天是星期五
高一数学必修1 第五章 三角函数
第1节 任意角
回顾旧知
静态定义:有公共端点的两射线组成的几何图形叫角.
(顶点)
(边)
(边)
动态定义:一条射线绕着它端点从一个位置旋转到另一个位置所成的图形叫做角.
始边
终边
旋转方向
1、角的定义
2、角的范围:
0°~360°
3、角的分类:
思考:角的范围可以超过吗?现实生活中有这样的例子吗?
“前空翻转体 540 度”
“后空翻转体 720 度”
OA绕点O旋转所成的角与O'B 绕点O'旋转所成的角就会有不同的方向.
钟表慢了 2 小时,校准后分针转过的角度
旋转度数+旋转方向
任意角的概念
平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形叫做角
始边:射线的起始位置;终边:射线的终止位置.
正角:一条射线绕其端点按逆时针方向旋转形成的角;
负角:一条射线绕其端点按顺时针方向旋转形成的角;
零角:一条射线没有做任何旋转,称它形成了一个零角。零角的始边与终边重合,如果零角,那么=0°.
旋转方向定符号,旋转量定大小(绝对值)
思考:如果图中,,你能读出下图中的各个角度吗?
在形成角的过程中,如果射线的旋转方向相同,且旋转量相等,则称这两个角相等。
若α与β相等,记为α=β。
设α,β 是任意两个角,规定:
α
β
α
α+β
β
加法:
把角α的终边旋转角β,这时终边所对应的角是α+β
在形成角的过程中,如果射线的旋转方向相反,且旋转量相等,则这两个角互为相反角。
α的相反角记为“-α”
设α,β 是任意两个角,规定:
减去一个角等于加上它的相反角,即α-β=α+(-β)
α
- β
α -β
减法:
练习: 若90 <α<β<135 ,
则α-β的范围是_______________,
α+β的范围是________________.
(-45 , 0 )
(180 , 270 )
为了方便,使角的顶点与原点重合,角的始边与x轴的非负半轴重合.
思考:角的终边可能落在哪些位置?
象限角
第一象限角
第二象限角
第三象限角
第四象限角
轴线角
角的终边在第几象限,那么这个角是第几象限角.
角的终边在坐标轴上,那么这个角不属于任何象限,习惯上称为轴线角.
象限角和轴线角
练习:-50°,405°,210°,-200°,-450°分别是第几象限角?是正角还是负角?
课本P171页练习1.锐角是第几象限角 第一象限角一定是锐角吗 再分别就直角、钝角来回答这两个问题。
课本P171页练习3.已知角的顶点与原点重合, 角的始边与x轴的非负半轴重合, 请作出下列各角,并指出它们各是哪个象限的角?
(1)420 , (2)-75 , (3)855 , (4) -510 .
第一象限角
420
-75
第四象限角
855
第二象限角
-510
第三象限角
解:
在直角坐标系中作出下列各角:
对于直角坐标系内的任意一条射线,以它为终边的角并不唯一。
思考:能不能用集合的形式将它们表达出来?
还有没有与-32°终边相同的角?
与-32°终边相同的角有无数多个,它们与-32°角均相差360°的整数倍,都可以表示成-32°的角与k(k∈Z)个周角的和.
因此与-32°终边相同的所有角可以表示为
β= -32°+k 360°,k∈Z.
一般地,我们有:
所有与角 终边相同的角,连同角 在内,可构成一个集合
S ={β|β= +k·360°, },
即任一与角 终边相同的角,都可以表示成角 与整数个周角的和.
注意:(1) k∈Z。
“k >0”表示β是将α的终边逆时针旋转得到的;
“k <0”表示β是将α的终边顺时针旋转得到的;
“k =0”表示β就是α本身。
(2)α是任意角;
(3)终边相同的角不一定相相等,它们有无数多个,它们
之间差相差360 的整数倍
例2:写出终边在y轴上的角的集合
例3 写出终边在直线y=x上的角的集合S,S中满足不等式
-360°≤ β <720°的元素β有哪些?
解 S={β|β=45 +k·180 ,k∈Z}.
S中适合不等式-360 ≤ β< 720 的元素有:
-315 ,-135 , 45 , 225 , 405 , 585 .
小结
课本P171页练习2. 今天是星期三, 则7k(k∈Z)天后的那一天是星期几 7k(k∈Z)天前的那一天是星期几 100天后的那一天是星期几
7k(k∈Z)天后和7k天前的那一天都是星期三
∵100=14×7+2
∴100天后的那一天是星期五
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
