6.3 余角、补角、对顶角 教学课件(共14张PPT) 2023--2024学年苏科版七年级数学上册
文档属性
| 名称 | 6.3 余角、补角、对顶角 教学课件(共14张PPT) 2023--2024学年苏科版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 00:25:30 | ||
图片预览






文档简介
(共14张PPT)
6.3余角、补角、对顶角
(第一课时)
苏科版七年级上册 数学
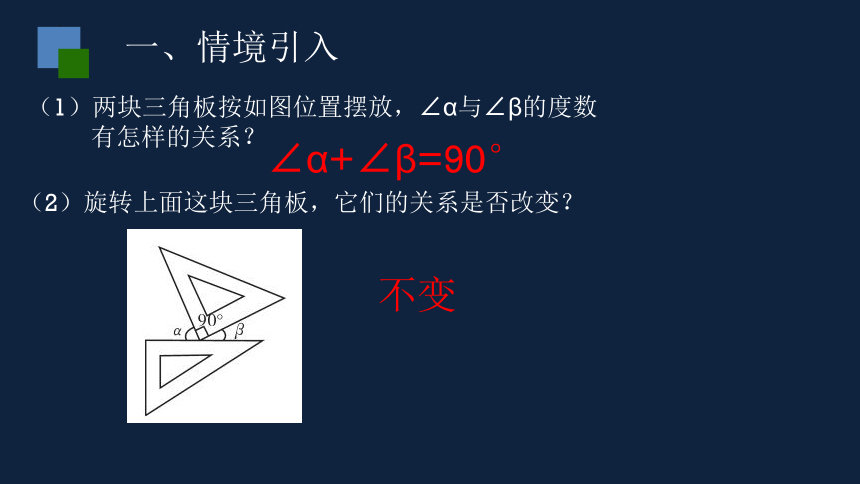
一、情境引入
(1)两块三角板按如图位置摆放,∠α与∠β的度数
有怎样的关系?
(2)旋转上面这块三角板,它们的关系是否改变?
∠α+∠β=90°
不变
二、知识建构
1、余角的定义:
如果两个角的和是一个直角,那么这两个角互为余角,简称互余,其中的一个角叫做另一个角的余角.
想一想:
①如何理解“互为”?
你还能联想到我们学过的什么知识?
②把互余的两个角分开放,它们还互余吗?
注:“互余”是两个角之间的数量关系,与位置无关.
几何语言:
反之:
∵∠1+∠2=90°
∴∠1与∠2互余
∵∠1与∠2互余
∴∠1+∠2=90°
填一填:
50°
45°
60°
n°
40°
45°
30°
(90-n)°
∠α
∠α的余角
探索活动:
1、借助直角三角板,以O为顶点画出下图中
∠BOC的余角.
2、找出图中互余的角: .
3、找出图中相等的角(直角除外): .
4、你能用一句话概括上面的结论吗?
∠1与∠2,∠1与∠3
∠2与∠3
结论:
同角的余角相等.
若∠1=∠2,∠1与∠3互余,∠2与∠4互余,
那么∠3与∠4有什么数量关系?
想一想:
解:因为∠1与∠3互余, ∠2与∠4互余,
所以∠1+∠3=90°,∠2+∠4=90°.
即∠3=90°-∠1,∠4=90°-∠2.
因为∠1=∠2,
所以∠3=∠4.
你能用一句话概括上面的结论吗?
结论: 等角 的余角相等.
同角( )
三、类比学习
∠α+∠β=180°
若两块三角板按照下图的方式摆放,∠α与∠β有怎样的数量关系?
补角的定义:
如果两个角的和是一个平角,那么这两个角互为补角,简称互补,其中一个角叫做另一个角的补角.
注:“互补”也是两个角之间的数量关系,
与位置无关.
几何语言:
反之:
∵∠3+∠4=180°
∴∠3与∠4互补
∵∠3与∠4互补
∴∠3+∠4=180°
补角的性质:同角(等角 )的补角相等.
类比余角的xi性质,你能得到补角的性质吗?
已知:∠1与∠2互补,∠1与∠3互补,
求证:∠2=∠3
证明:因为∠1与∠2互补,
所以∠1+∠2=180°,
所以∠2=180°-∠1.
因为∠1与∠3互补,
所以∠1+∠3=180°,
所以∠3=180°-∠1.
所以∠2=∠3.
填一填:
50°
45°
60°
n°
40°
45°
30°
(90-n)°
130°
135°
120°
(180-n)°
思考:同一个角的补角与它的余角之间有怎样的数量关系?
一个角的补角比这个角的余角大90°.
∠α的余角
∠α的补角
∠α
解:
三、例题讲解
例、已知∠α与∠β互为补角,且∠β比∠α大30°.求∠α、∠β的度数.
根据题意,可得∠β=∠α+30°.
因为∠α与∠β互为补角,
所以∠α+∠β=180°,
所以∠α+(∠α+30°)=180°,
所以∠α=75°,
所以∠β=75°+30°=105°.
图1
图2
同角的余角相等
等角的补角相等
四、课堂练习
1、如图1,∠AOC=90°,∠BOD=90°, 则∠AOB与∠COD的关系是__________,理由是:_____________.
∠AOB=∠COD
2、如图2,∠AOB+∠BOC=180°,∠AOD+∠COD=180°,若∠AOB=∠AOD,则∠BOC与∠BOD的关系是____________,理由是____________.
∠BOC=∠COD
互余的角:
∠COD与∠COE、
∠COD与∠BOE、
∠AOD与∠COE、
∠AOD与∠BOE.
互补的角:
∠AOD与∠BOD、
∠AOC与∠BOC、
∠AOE与∠BOE、
∠COD与∠BOD、
∠AOE与∠COE.
3、已知,如图,A、O、B在同一条直线上,射线OD、OE分别平分∠AOC和∠BOC,图中有哪些互余的角?有哪些互补的角?
五、课堂小结
1、你收获了哪些数学知识?
2、你学会了哪些数学方法?
3、你还想继续研究什么?
余角
定义、
性质
补角
类比
定义、
性质
6.3余角、补角、对顶角
(第一课时)
苏科版七年级上册 数学
一、情境引入
(1)两块三角板按如图位置摆放,∠α与∠β的度数
有怎样的关系?
(2)旋转上面这块三角板,它们的关系是否改变?
∠α+∠β=90°
不变
二、知识建构
1、余角的定义:
如果两个角的和是一个直角,那么这两个角互为余角,简称互余,其中的一个角叫做另一个角的余角.
想一想:
①如何理解“互为”?
你还能联想到我们学过的什么知识?
②把互余的两个角分开放,它们还互余吗?
注:“互余”是两个角之间的数量关系,与位置无关.
几何语言:
反之:
∵∠1+∠2=90°
∴∠1与∠2互余
∵∠1与∠2互余
∴∠1+∠2=90°
填一填:
50°
45°
60°
n°
40°
45°
30°
(90-n)°
∠α
∠α的余角
探索活动:
1、借助直角三角板,以O为顶点画出下图中
∠BOC的余角.
2、找出图中互余的角: .
3、找出图中相等的角(直角除外): .
4、你能用一句话概括上面的结论吗?
∠1与∠2,∠1与∠3
∠2与∠3
结论:
同角的余角相等.
若∠1=∠2,∠1与∠3互余,∠2与∠4互余,
那么∠3与∠4有什么数量关系?
想一想:
解:因为∠1与∠3互余, ∠2与∠4互余,
所以∠1+∠3=90°,∠2+∠4=90°.
即∠3=90°-∠1,∠4=90°-∠2.
因为∠1=∠2,
所以∠3=∠4.
你能用一句话概括上面的结论吗?
结论: 等角 的余角相等.
同角( )
三、类比学习
∠α+∠β=180°
若两块三角板按照下图的方式摆放,∠α与∠β有怎样的数量关系?
补角的定义:
如果两个角的和是一个平角,那么这两个角互为补角,简称互补,其中一个角叫做另一个角的补角.
注:“互补”也是两个角之间的数量关系,
与位置无关.
几何语言:
反之:
∵∠3+∠4=180°
∴∠3与∠4互补
∵∠3与∠4互补
∴∠3+∠4=180°
补角的性质:同角(等角 )的补角相等.
类比余角的xi性质,你能得到补角的性质吗?
已知:∠1与∠2互补,∠1与∠3互补,
求证:∠2=∠3
证明:因为∠1与∠2互补,
所以∠1+∠2=180°,
所以∠2=180°-∠1.
因为∠1与∠3互补,
所以∠1+∠3=180°,
所以∠3=180°-∠1.
所以∠2=∠3.
填一填:
50°
45°
60°
n°
40°
45°
30°
(90-n)°
130°
135°
120°
(180-n)°
思考:同一个角的补角与它的余角之间有怎样的数量关系?
一个角的补角比这个角的余角大90°.
∠α的余角
∠α的补角
∠α
解:
三、例题讲解
例、已知∠α与∠β互为补角,且∠β比∠α大30°.求∠α、∠β的度数.
根据题意,可得∠β=∠α+30°.
因为∠α与∠β互为补角,
所以∠α+∠β=180°,
所以∠α+(∠α+30°)=180°,
所以∠α=75°,
所以∠β=75°+30°=105°.
图1
图2
同角的余角相等
等角的补角相等
四、课堂练习
1、如图1,∠AOC=90°,∠BOD=90°, 则∠AOB与∠COD的关系是__________,理由是:_____________.
∠AOB=∠COD
2、如图2,∠AOB+∠BOC=180°,∠AOD+∠COD=180°,若∠AOB=∠AOD,则∠BOC与∠BOD的关系是____________,理由是____________.
∠BOC=∠COD
互余的角:
∠COD与∠COE、
∠COD与∠BOE、
∠AOD与∠COE、
∠AOD与∠BOE.
互补的角:
∠AOD与∠BOD、
∠AOC与∠BOC、
∠AOE与∠BOE、
∠COD与∠BOD、
∠AOE与∠COE.
3、已知,如图,A、O、B在同一条直线上,射线OD、OE分别平分∠AOC和∠BOC,图中有哪些互余的角?有哪些互补的角?
五、课堂小结
1、你收获了哪些数学知识?
2、你学会了哪些数学方法?
3、你还想继续研究什么?
余角
定义、
性质
补角
类比
定义、
性质
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
