6.3余角、补角、对顶角(2)课件 2023—2024学年苏科版数学七年级上册(14张PPT)
文档属性
| 名称 | 6.3余角、补角、对顶角(2)课件 2023—2024学年苏科版数学七年级上册(14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 08:33:08 | ||
图片预览




文档简介
(共14张PPT)
6.3余角、补角、对顶角
(第二课时)
苏科版七年级上册 数学
一、复习回顾
如图,O为直线AB上一点,∠AOD=900,
则图中哪些角互为余角?哪些角互为补角?
O
A
D
C
B
互余:
∠COD与∠BOC
∠AOD与∠BOD
∠AOC与∠BOC
互补:
2.
∠2=∠3
同角的余角相等
∠2=∠4
等角的补角相等
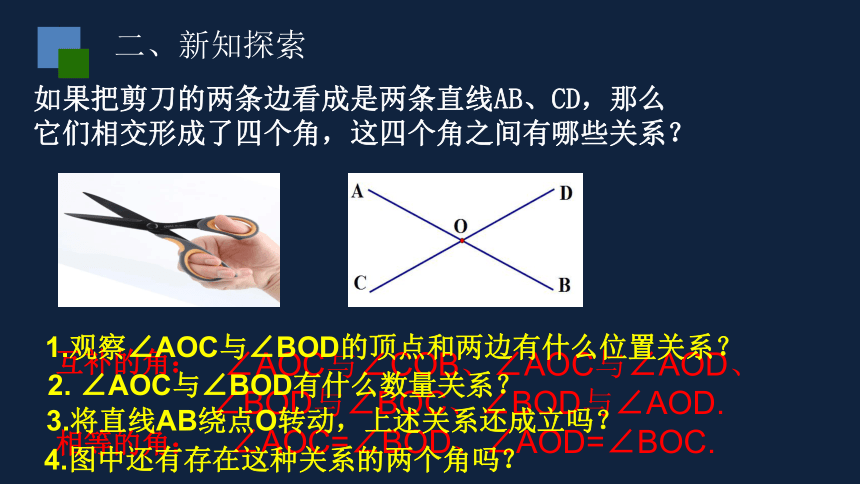
如果把剪刀的两条边看成是两条直线AB、CD,那么它们相交形成了四个角,这四个角之间有哪些关系?
二、新知探索
∠AOC与∠COB、∠AOC与∠AOD、
∠BOD与∠BOC、∠BOD与∠AOD.
∠AOC=∠BOD、∠AOD=∠BOC.
互补的角:
相等的角:
1.观察∠AOC与∠BOD的顶点和两边有什么位置关系?
2. ∠AOC与∠BOD有什么数量关系?
3.将直线AB绕点O转动,上述关系还成立吗?
4.图中还有存在这种关系的两个角吗?
1.对顶角的定义:
两条直线相交形成4个角:∠AOC、∠BOC、
∠BOD、∠AOD,其中OB是OA的反向延长线,
OD是OC的反向延长线,我们把∠AOC和∠BOD
叫做对顶角.∠BOC和∠AOD也是对顶角.
注:对顶角是两个角之间
的位置关系.
2.对顶角的性质:
对顶角相等.
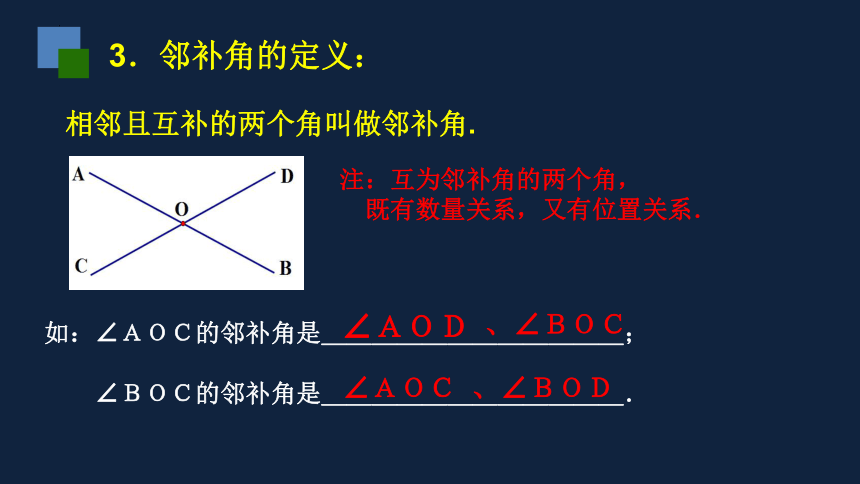
3.邻补角的定义:
相邻且互补的两个角叫做邻补角.
如:∠AOC的邻补角是____________;
∠BOC的邻补角是____________.
∠AOD
∠AOC
注:互为邻补角的两个角,
既有数量关系,又有位置关系.
、∠BOC
、∠BOD
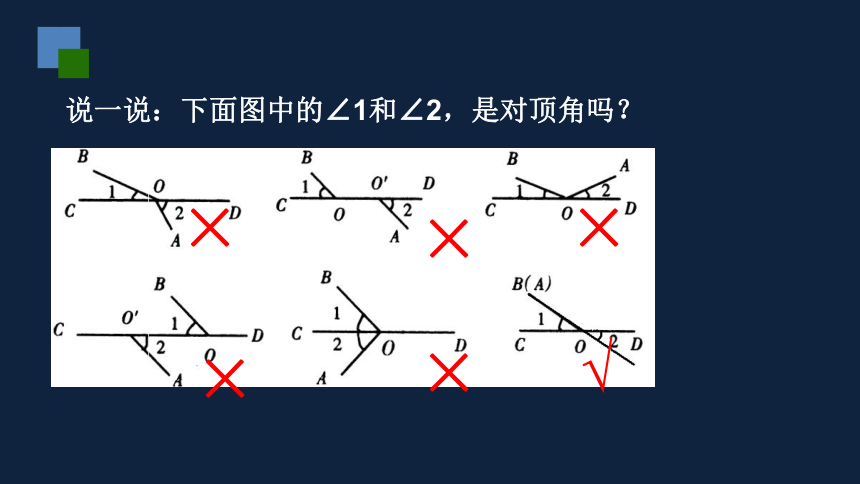
说一说:下面图中的∠1和∠2,是对顶角吗?
×
×
×
×
×
√
例. 如图,直线AB、CD相交于点O,∠BOD与∠BOE互为余角,∠AOC=72°.求∠BOE的度数.
三、灵活运用
解: 因为∠AOC与∠BOD是对顶角,
所以∠BOD=∠AOC=72°.
又因为∠BOD与∠BOE互为余角,
所以∠BOD+∠BOE=90°.
所以∠BOE=90°-∠BOD
=90°-72°
=18°.
1. 如图,直线AC、DE相交于点O,OE是∠AOB
的角平分线,∠COD=500,试求∠AOB的度数.
C
O
A
B
D
E
解: 因为∠AOE与∠COD是对顶角,
所以∠AOE=∠COD=50°.
因为OE是∠AOB的角平分线,
所以∠AOB=2∠AOE
=2×50°
=100°.
2.如图,直线AB、EF相交于点D,∠ADC=900。
(1)∠1的对顶角是________;∠2的余角有_______________。
(2)若∠1与∠2的度数之比为1︰4, 求∠BDF的度数。
A
B
F
C
E
D
1
2
∠BDF
∠ 1
和∠BDF
解:因为∠ADC=90°,
所以∠1+∠2=90°.
因为∠1:∠2=1 : 4,
因为∠BDF与∠1是对顶角,
所以∠BDF=∠1=18°.
2条直线交于一点
3条直线交于一点
4条直线交于一点
____对对顶角
5条直线交于一点
若有n条直线相交于一点O,那么有__________对对顶角.
n(n-1)
6
12
20
3. 数一数
____对对顶角
____对对顶角
____对对顶角
2
4. 你能用折纸的方式折出对顶角吗?
A
B
C
D
O
5. 要测量两堵墙所成的∠AOB的度数,
但人不能进入围墙,该如何测量呢?
O
A
B
O
C
D
法一:利用邻补角
法二:利用对顶角
四、课堂小结
角
余角
补角
对顶角
两个角的数量关系
两个角的位置关系
……
你还想研究怎样的角呢?
邻补角
两个角的数量和位置关系
6.3余角、补角、对顶角
(第二课时)
苏科版七年级上册 数学
一、复习回顾
如图,O为直线AB上一点,∠AOD=900,
则图中哪些角互为余角?哪些角互为补角?
O
A
D
C
B
互余:
∠COD与∠BOC
∠AOD与∠BOD
∠AOC与∠BOC
互补:
2.
∠2=∠3
同角的余角相等
∠2=∠4
等角的补角相等
如果把剪刀的两条边看成是两条直线AB、CD,那么它们相交形成了四个角,这四个角之间有哪些关系?
二、新知探索
∠AOC与∠COB、∠AOC与∠AOD、
∠BOD与∠BOC、∠BOD与∠AOD.
∠AOC=∠BOD、∠AOD=∠BOC.
互补的角:
相等的角:
1.观察∠AOC与∠BOD的顶点和两边有什么位置关系?
2. ∠AOC与∠BOD有什么数量关系?
3.将直线AB绕点O转动,上述关系还成立吗?
4.图中还有存在这种关系的两个角吗?
1.对顶角的定义:
两条直线相交形成4个角:∠AOC、∠BOC、
∠BOD、∠AOD,其中OB是OA的反向延长线,
OD是OC的反向延长线,我们把∠AOC和∠BOD
叫做对顶角.∠BOC和∠AOD也是对顶角.
注:对顶角是两个角之间
的位置关系.
2.对顶角的性质:
对顶角相等.
3.邻补角的定义:
相邻且互补的两个角叫做邻补角.
如:∠AOC的邻补角是____________;
∠BOC的邻补角是____________.
∠AOD
∠AOC
注:互为邻补角的两个角,
既有数量关系,又有位置关系.
、∠BOC
、∠BOD
说一说:下面图中的∠1和∠2,是对顶角吗?
×
×
×
×
×
√
例. 如图,直线AB、CD相交于点O,∠BOD与∠BOE互为余角,∠AOC=72°.求∠BOE的度数.
三、灵活运用
解: 因为∠AOC与∠BOD是对顶角,
所以∠BOD=∠AOC=72°.
又因为∠BOD与∠BOE互为余角,
所以∠BOD+∠BOE=90°.
所以∠BOE=90°-∠BOD
=90°-72°
=18°.
1. 如图,直线AC、DE相交于点O,OE是∠AOB
的角平分线,∠COD=500,试求∠AOB的度数.
C
O
A
B
D
E
解: 因为∠AOE与∠COD是对顶角,
所以∠AOE=∠COD=50°.
因为OE是∠AOB的角平分线,
所以∠AOB=2∠AOE
=2×50°
=100°.
2.如图,直线AB、EF相交于点D,∠ADC=900。
(1)∠1的对顶角是________;∠2的余角有_______________。
(2)若∠1与∠2的度数之比为1︰4, 求∠BDF的度数。
A
B
F
C
E
D
1
2
∠BDF
∠ 1
和∠BDF
解:因为∠ADC=90°,
所以∠1+∠2=90°.
因为∠1:∠2=1 : 4,
因为∠BDF与∠1是对顶角,
所以∠BDF=∠1=18°.
2条直线交于一点
3条直线交于一点
4条直线交于一点
____对对顶角
5条直线交于一点
若有n条直线相交于一点O,那么有__________对对顶角.
n(n-1)
6
12
20
3. 数一数
____对对顶角
____对对顶角
____对对顶角
2
4. 你能用折纸的方式折出对顶角吗?
A
B
C
D
O
5. 要测量两堵墙所成的∠AOB的度数,
但人不能进入围墙,该如何测量呢?
O
A
B
O
C
D
法一:利用邻补角
法二:利用对顶角
四、课堂小结
角
余角
补角
对顶角
两个角的数量关系
两个角的位置关系
……
你还想研究怎样的角呢?
邻补角
两个角的数量和位置关系
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
