第四章 基本平面图形复习课 2023-2024学年北师大版七年级上册数学(28张PPT)
文档属性
| 名称 | 第四章 基本平面图形复习课 2023-2024学年北师大版七年级上册数学(28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
第四章 基本平面图形
复习课
一、学习目标
1.掌握线段、射线、直线、角、多边形、圆等平面图形的概念,
会用正确的方法表示线段、角等.
2.会比较线段(或角)的大小.
3.会进行有关线段、角度的计算.(重点)
4.会计算扇形圆心角的度数和面积.
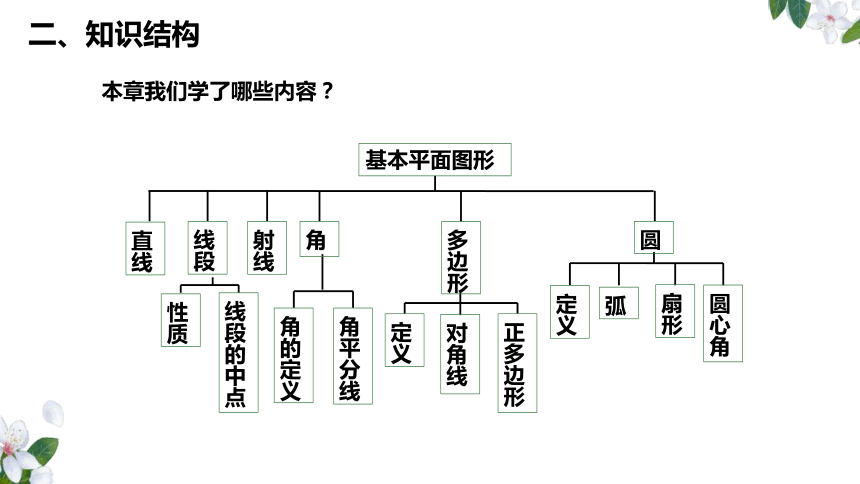
本章我们学了哪些内容?
基本平面图形
直线
线段
射线
圆
角
多边形
性质
线段的中点
角的定义
定义
对角线
圆心角
扇形
弧
定义
正多边形
角平分线
二、知识结构
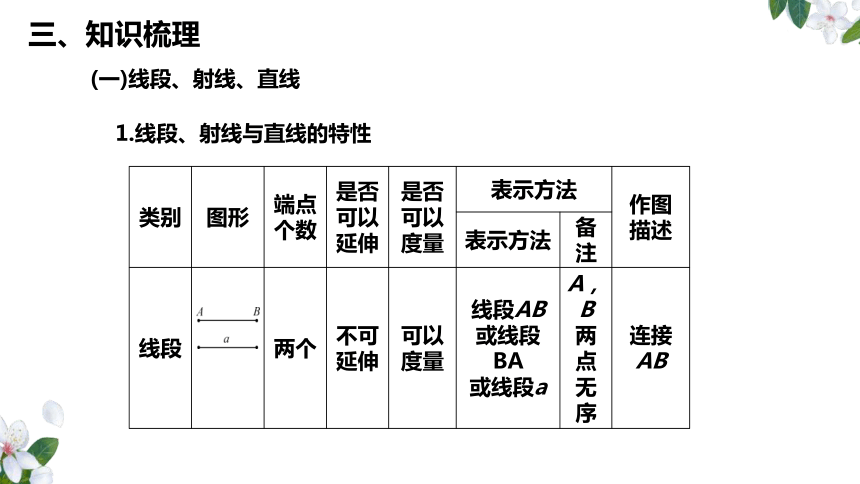
(一)线段、射线、直线
1.线段、射线与直线的特性
连接AB
A,B
两点
无序
线段AB
或线段BA
或线段a
可以
度量
不可
延伸
两个
线段
备注
表示方法
作图
描述
表示方法
是否
可以
度量
是否
可以
延伸
端点
个数
图形
类别
三、知识梳理
过A,B两点
作直线AB
A,B
两点
无序
直线
AB
或直
线BA
或直线a
不能
度量
向两个
方向延伸
无
直线
以A为端点
作射线
AB
A,B
两点
有序,
端点
在前
射线
AB
不能
度量
向一个
方向延伸
一个
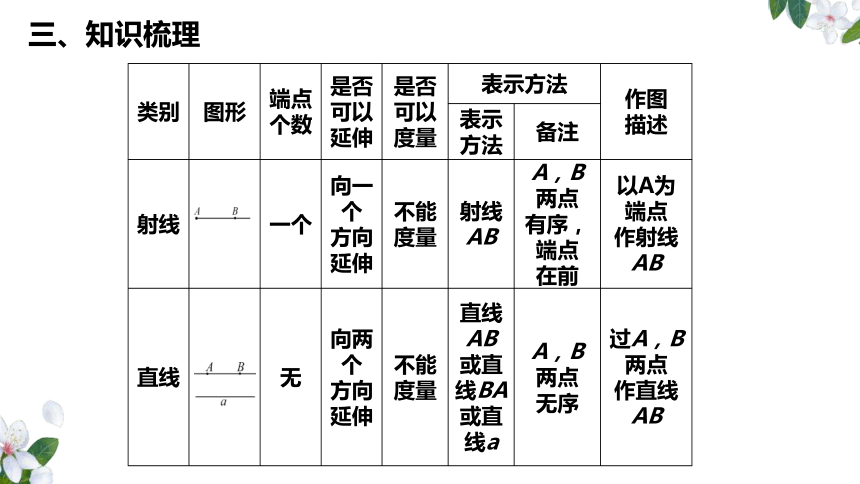
射线
备注
表示
方法
作图
描述
表示方法
是否
可以
度量
是否
可以
延伸
端点
个数
图形
类别
三、知识梳理
2.两点确定一条直线
经过两点有且只有一条直线.
三、知识梳理
(二)比较线段的长度
1.线段的性质
两点之间的所有连线中,线段________ .简述为:两点之间,线段________ .
最短
最短
三、知识梳理
两点之间的距离是指连接两点的线段的________ .
长度
2.两点之间的距离
3.比较两条线段的长短
(1)直接观察法;(2)度量法;(3)叠合法.
4.线段的中点
点M将线段AB分成_______的两条线段AM与BM,点M叫做线段AB的中点.
相等
三、知识梳理
(三)角
1.角的定义
(1)角是由两条具有公共端点的射线组成的图形.
(2)角可以看做是一条射线绕着它的端点旋转而成.
2.角的表示方法
表示方法 注意事项
用三个大写的字母表示 表示顶点的字母要写在中间
用一个顶点的字母来表示 一个字母只表示一个角
用一个希腊字母(数字)表示 在靠近顶点处画上弧线,并写上希腊字母(数字)
三、知识梳理
3.平角与周角的概念
一条射线绕它的端点旋转,当终边和始边成一条直线时,所成的角叫做________;终边继续旋转,当它又和始边________时,所成的角叫做周角.平角为180°,周角为360°.
重合
平角
三、知识梳理
4.角的度量
(1)角的度量单位是度、分、秒.
(2)它们之间的关系是六十进制的,即1°=60′,1′=60″.
三、知识梳理
1.角的比较方法
(1)直接观察法;(2)度量法;(3)叠合法.
(四)角的比较
2.角的平分线
从一个角的顶点引出的一条射线,把这个角分成__________的角,这条射线叫做这个角的平分线.
两个相等
三、知识梳理
(五)多边形和圆的初步认识
1.多边形
(1)多边形是由若干条不在同一直线上的________首尾顺次相连组成的封闭____________ .
(2)连接多边形不相邻的两个顶点的线段叫做多边形的________ .
(3)n边形对角线的条数____________条.
对角线
线段
平面图形
2.正多边形
各边相等,各角也相等的多边形叫做正多边形.
三、知识梳理
3.圆的有关概念
(1)在平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做______ .固定的端点称为_____ ,这条线段称_______.
(2)圆上任意两点间的部分叫做圆弧,简称弧.
(3)由一条弧和经过这条弧上的端点的两条半径所组成的图形叫______.
(4)顶点在圆心的角叫做________ .
(5)扇形的面积: .
圆心角
圆
圆心
半径
扇形
三、知识梳理
例1.如图,A,B,C,D为平面内每三点都不在一条直线上的四点,那么过其中任意的两点,可画出几条直线?若A,B,C,D,E为平面内每三点都不在一条直线上的五点,则过其中任意的两点可画几条直线?若是n个点呢?
四、典型例题
考点一 图形个数问题
对于已知五点,类似地可以得到 =10(条).
对于n个点,就可得到= (条).
解:对于已知四点,A点与其他三点共可确定3条直线,过B,C,D也各有3条,这样共有4×3=12(条)直线,但每条都重复一次,所以应该是 =6(条).
四、典型例题
我们在探索物体的个数时,可首先求出各图中物体的个数,将其与相应的图序数作对比,看二者有何关系,即得规律.
归纳总结
四、典型例题
1.分别以点A,B,C,D,E,F为端点的线段共有几条?分别把它们写出来.
解:图中分别以点A,B,C,D,E,F为端点的线段共有14条,分别为线段AB,AC,AD,AE,BC,BD,BE,BF,CD,CE,CF,DE,DF,EF.
【当堂检测】
例2.如图,线段AB=32cm,点C在AB上,且AC∶CB=5∶3,点D是AC的中点,点O是AB的中点,求DB与OC的长.
考点二 线段长度的计算
【解析】 从图上可以看出DB=AB-AD,而D是AC的中点,AD= AC,结合AC∶CB=5∶3,AB=32 cm,故AC和BC可求,OC=OB-BC= AB-BC.
四、典型例题
解:因为AC∶CB=5∶3,AC+CB=AB,
所以AC= AB= = 20 (cm),
BC= AB= =12 (cm).
因为D是AC的中点,所以AD= AC=10 (cm),
所以DB=AB-AD=32-10=22(cm).
因为O是AB的中点,所以OB= AB=16(cm) ,
所以OC=OB-BC=16-12=4(cm),
所以DB=22 cm,OC=4 cm.
四、典型例题
2.如图,AB=8 cm,O为线段AB上的任意一点, C为AO的中点,D为OB的中点,你能求出线段CD的长度吗?请说明理由.
解:能.理由:
因为C为AO的中点,D为OB的中点,
所以CD=CO+OD= (AO+OB)= AB= ×8=4(cm).
【当堂检测】
例3.如图,点O在直线AB上,射线OC平分∠DOB.若∠DOC=35°,则∠AOD等于( )
考点三 角平分线的计算
A.35° B.70° C.110° D.145°
解:∠DOB=2∠DOC=70°,∠DOB+∠AOD=180°,则∠AOD=110°,故选C.
C
四、典型例题
3.如图,∠AOC=15°,∠BOC=45°,
OD平分∠AOB,求∠COD的度数.
解:因为OD平分∠AOB,
所以∠BOD=∠AOB
= (∠BOC+∠AOC)
= (45°+15°)=30°,
所以∠COD=∠BOC-∠BOD=45°-30°=15°.
【当堂检测】
例4.某实验中学九年级(1)班全体同学的综合素质评价“运动与健康”方面的等级统计如图3所示,其中评价为“A”所在扇形的圆心角是多少度.
解:A部分占的百分比为:1-35%-20%-15%=30%,
因此A所在扇形的圆心角的度数为360°×30%=108°.
考点四:多边形和圆
图3
四、典型例题
4.已知一个扇形的圆心角的度数为150°,半径长为3,则这个扇形的面积为多少.(结果保留π)
解:因为扇形所在圆的面积为S=π×32=9π,
所以S扇形= S= ×9π= π.
【当堂检测】
例5.从一个多边形的任何一个顶点出发都只有5条对角线,则它的边数是多少?
解:设这个多边形是n边形.
依题意,得n-3=5,
解得n=8.
故这个多边形的边数是8.
考点五:多边形
四、典型例题
5.若某一个顶点与和它不相邻的其他各顶点连接,可将多边形分成七个三角形,则这个多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
解析:从n边形的一个顶点出发的对角线把n边形分成(n-2)个三角形,则将多边形分成七个三角形对应的多边形是九边形.故选D.
【当堂检测】
D
五、课堂总结
第四章 基本平面图形
复习课
一、学习目标
1.掌握线段、射线、直线、角、多边形、圆等平面图形的概念,
会用正确的方法表示线段、角等.
2.会比较线段(或角)的大小.
3.会进行有关线段、角度的计算.(重点)
4.会计算扇形圆心角的度数和面积.
本章我们学了哪些内容?
基本平面图形
直线
线段
射线
圆
角
多边形
性质
线段的中点
角的定义
定义
对角线
圆心角
扇形
弧
定义
正多边形
角平分线
二、知识结构
(一)线段、射线、直线
1.线段、射线与直线的特性
连接AB
A,B
两点
无序
线段AB
或线段BA
或线段a
可以
度量
不可
延伸
两个
线段
备注
表示方法
作图
描述
表示方法
是否
可以
度量
是否
可以
延伸
端点
个数
图形
类别
三、知识梳理
过A,B两点
作直线AB
A,B
两点
无序
直线
AB
或直
线BA
或直线a
不能
度量
向两个
方向延伸
无
直线
以A为端点
作射线
AB
A,B
两点
有序,
端点
在前
射线
AB
不能
度量
向一个
方向延伸
一个
射线
备注
表示
方法
作图
描述
表示方法
是否
可以
度量
是否
可以
延伸
端点
个数
图形
类别
三、知识梳理
2.两点确定一条直线
经过两点有且只有一条直线.
三、知识梳理
(二)比较线段的长度
1.线段的性质
两点之间的所有连线中,线段________ .简述为:两点之间,线段________ .
最短
最短
三、知识梳理
两点之间的距离是指连接两点的线段的________ .
长度
2.两点之间的距离
3.比较两条线段的长短
(1)直接观察法;(2)度量法;(3)叠合法.
4.线段的中点
点M将线段AB分成_______的两条线段AM与BM,点M叫做线段AB的中点.
相等
三、知识梳理
(三)角
1.角的定义
(1)角是由两条具有公共端点的射线组成的图形.
(2)角可以看做是一条射线绕着它的端点旋转而成.
2.角的表示方法
表示方法 注意事项
用三个大写的字母表示 表示顶点的字母要写在中间
用一个顶点的字母来表示 一个字母只表示一个角
用一个希腊字母(数字)表示 在靠近顶点处画上弧线,并写上希腊字母(数字)
三、知识梳理
3.平角与周角的概念
一条射线绕它的端点旋转,当终边和始边成一条直线时,所成的角叫做________;终边继续旋转,当它又和始边________时,所成的角叫做周角.平角为180°,周角为360°.
重合
平角
三、知识梳理
4.角的度量
(1)角的度量单位是度、分、秒.
(2)它们之间的关系是六十进制的,即1°=60′,1′=60″.
三、知识梳理
1.角的比较方法
(1)直接观察法;(2)度量法;(3)叠合法.
(四)角的比较
2.角的平分线
从一个角的顶点引出的一条射线,把这个角分成__________的角,这条射线叫做这个角的平分线.
两个相等
三、知识梳理
(五)多边形和圆的初步认识
1.多边形
(1)多边形是由若干条不在同一直线上的________首尾顺次相连组成的封闭____________ .
(2)连接多边形不相邻的两个顶点的线段叫做多边形的________ .
(3)n边形对角线的条数____________条.
对角线
线段
平面图形
2.正多边形
各边相等,各角也相等的多边形叫做正多边形.
三、知识梳理
3.圆的有关概念
(1)在平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做______ .固定的端点称为_____ ,这条线段称_______.
(2)圆上任意两点间的部分叫做圆弧,简称弧.
(3)由一条弧和经过这条弧上的端点的两条半径所组成的图形叫______.
(4)顶点在圆心的角叫做________ .
(5)扇形的面积: .
圆心角
圆
圆心
半径
扇形
三、知识梳理
例1.如图,A,B,C,D为平面内每三点都不在一条直线上的四点,那么过其中任意的两点,可画出几条直线?若A,B,C,D,E为平面内每三点都不在一条直线上的五点,则过其中任意的两点可画几条直线?若是n个点呢?
四、典型例题
考点一 图形个数问题
对于已知五点,类似地可以得到 =10(条).
对于n个点,就可得到= (条).
解:对于已知四点,A点与其他三点共可确定3条直线,过B,C,D也各有3条,这样共有4×3=12(条)直线,但每条都重复一次,所以应该是 =6(条).
四、典型例题
我们在探索物体的个数时,可首先求出各图中物体的个数,将其与相应的图序数作对比,看二者有何关系,即得规律.
归纳总结
四、典型例题
1.分别以点A,B,C,D,E,F为端点的线段共有几条?分别把它们写出来.
解:图中分别以点A,B,C,D,E,F为端点的线段共有14条,分别为线段AB,AC,AD,AE,BC,BD,BE,BF,CD,CE,CF,DE,DF,EF.
【当堂检测】
例2.如图,线段AB=32cm,点C在AB上,且AC∶CB=5∶3,点D是AC的中点,点O是AB的中点,求DB与OC的长.
考点二 线段长度的计算
【解析】 从图上可以看出DB=AB-AD,而D是AC的中点,AD= AC,结合AC∶CB=5∶3,AB=32 cm,故AC和BC可求,OC=OB-BC= AB-BC.
四、典型例题
解:因为AC∶CB=5∶3,AC+CB=AB,
所以AC= AB= = 20 (cm),
BC= AB= =12 (cm).
因为D是AC的中点,所以AD= AC=10 (cm),
所以DB=AB-AD=32-10=22(cm).
因为O是AB的中点,所以OB= AB=16(cm) ,
所以OC=OB-BC=16-12=4(cm),
所以DB=22 cm,OC=4 cm.
四、典型例题
2.如图,AB=8 cm,O为线段AB上的任意一点, C为AO的中点,D为OB的中点,你能求出线段CD的长度吗?请说明理由.
解:能.理由:
因为C为AO的中点,D为OB的中点,
所以CD=CO+OD= (AO+OB)= AB= ×8=4(cm).
【当堂检测】
例3.如图,点O在直线AB上,射线OC平分∠DOB.若∠DOC=35°,则∠AOD等于( )
考点三 角平分线的计算
A.35° B.70° C.110° D.145°
解:∠DOB=2∠DOC=70°,∠DOB+∠AOD=180°,则∠AOD=110°,故选C.
C
四、典型例题
3.如图,∠AOC=15°,∠BOC=45°,
OD平分∠AOB,求∠COD的度数.
解:因为OD平分∠AOB,
所以∠BOD=∠AOB
= (∠BOC+∠AOC)
= (45°+15°)=30°,
所以∠COD=∠BOC-∠BOD=45°-30°=15°.
【当堂检测】
例4.某实验中学九年级(1)班全体同学的综合素质评价“运动与健康”方面的等级统计如图3所示,其中评价为“A”所在扇形的圆心角是多少度.
解:A部分占的百分比为:1-35%-20%-15%=30%,
因此A所在扇形的圆心角的度数为360°×30%=108°.
考点四:多边形和圆
图3
四、典型例题
4.已知一个扇形的圆心角的度数为150°,半径长为3,则这个扇形的面积为多少.(结果保留π)
解:因为扇形所在圆的面积为S=π×32=9π,
所以S扇形= S= ×9π= π.
【当堂检测】
例5.从一个多边形的任何一个顶点出发都只有5条对角线,则它的边数是多少?
解:设这个多边形是n边形.
依题意,得n-3=5,
解得n=8.
故这个多边形的边数是8.
考点五:多边形
四、典型例题
5.若某一个顶点与和它不相邻的其他各顶点连接,可将多边形分成七个三角形,则这个多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
解析:从n边形的一个顶点出发的对角线把n边形分成(n-2)个三角形,则将多边形分成七个三角形对应的多边形是九边形.故选D.
【当堂检测】
D
五、课堂总结
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
