6.5 垂直(1) 课件 (共14张PPT)2023—2024学年苏科版数学七年级上册
文档属性
| 名称 | 6.5 垂直(1) 课件 (共14张PPT)2023—2024学年苏科版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 00:00:00 | ||
图片预览



文档简介
(共14张PPT)
6.5 垂直(1)
苏科版八年级上册 数学
认识垂线
平面图形的认识
线段、射线、直线
角
…
概念:在同一平面内,不相交的两条直线叫做平行线
平行线的表示:用“//”表示平行
找或画平行线的方法:
(1)平面内:一放、二靠、三推、四画.
(2)网格内:关注线的走势(所在的长方形或直角三角形)
平行线
基本事实:过直线外一点有且只有一条直线与已知直线平行
b
a
相交
垂直
认识垂线
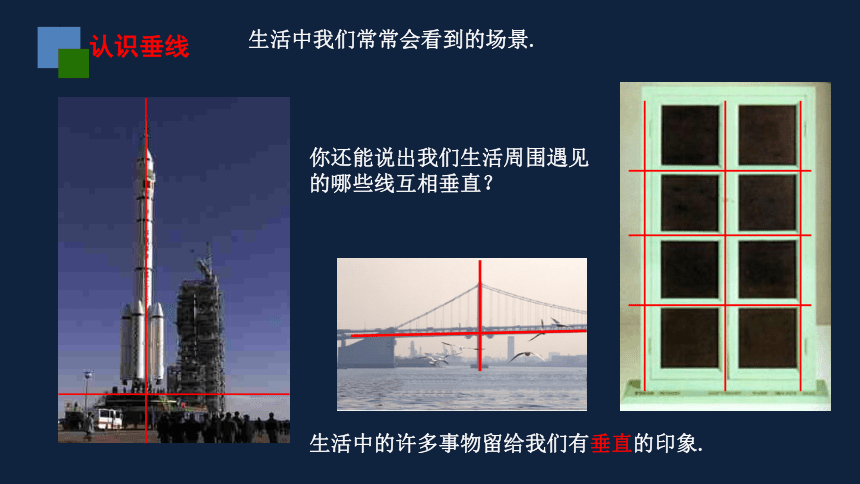
生活中我们常常会看到的场景.
生活中的许多事物留给我们有垂直的印象.
你还能说出我们生活周围遇见的哪些线互相垂直?
a
b
(普通相交)
a
b
O
A
B
D
C
(特殊相交):垂直
认识垂线
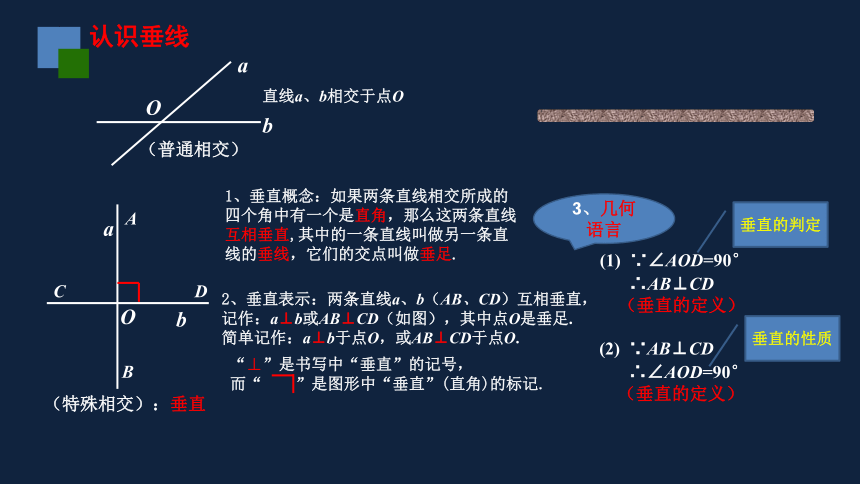
直线a、b相交于点O
2、垂直表示:两条直线a、b(AB、CD)互相垂直,
记作:a⊥b或AB⊥CD(如图),其中点O是垂足.
简单记作:a⊥b于点O,或AB⊥CD于点O.
“⊥”是书写中“垂直”的记号,
而“ ”是图形中“垂直”(直角)的标记.
(1) ∵∠AOD=90°
∴AB⊥CD
(垂直的定义)
(2) ∵AB⊥CD
∴∠AOD=90°
(垂直的定义)
垂直的判定
垂直的性质
3、几何
语言
O
1、垂直概念:如果两条直线相交所成的四个角中有一个是直角,那么这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
认识垂线
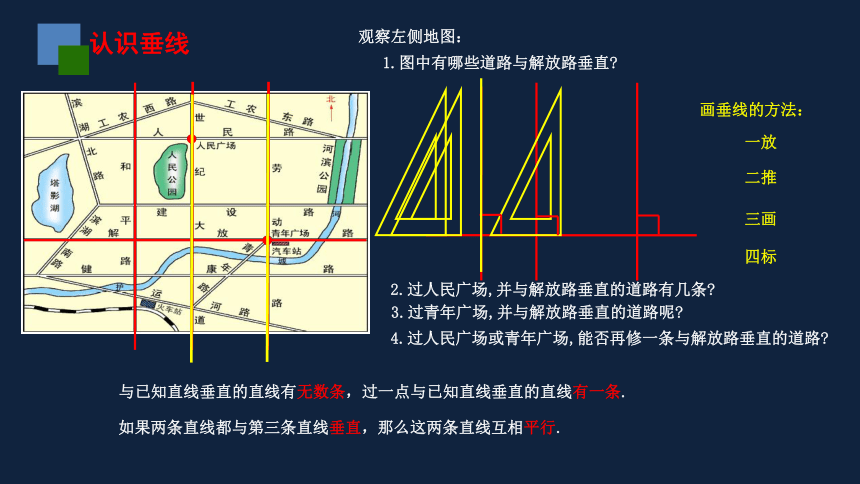
观察左侧地图:
1.图中有哪些道路与解放路垂直
2.过人民广场,并与解放路垂直的道路有几条
4.过人民广场或青年广场,能否再修一条与解放路垂直的道路
如果两条直线都与第三条直线垂直,那么这两条直线互相平行.
●
●
一放
二推
三画
画垂线的方法:
3.过青年广场,并与解放路垂直的道路呢
与已知直线垂直的直线有无数条,过一点与已知直线垂直的直线有一条.
四标
新知应用----典型例题
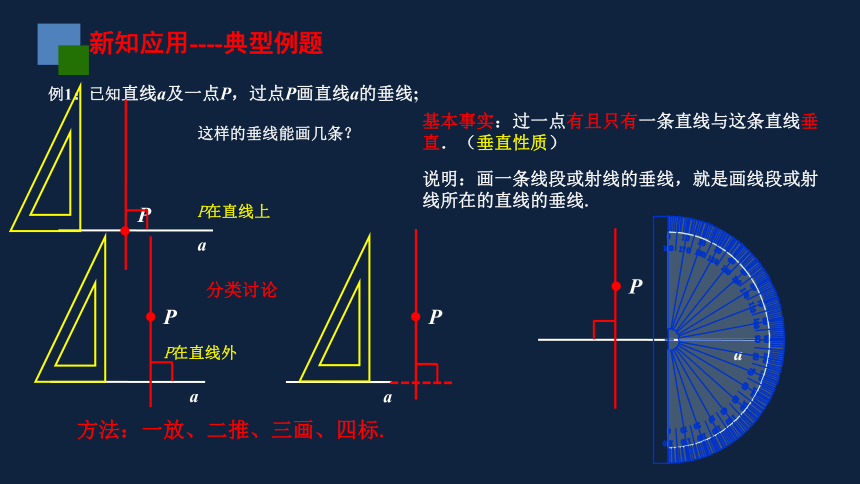
例1:已知直线a及一点P,过点P画直线a的垂线;
方法:一放、二推、三画、四标.
a
●
P
a
●
P
a
●
P
P在直线上
P在直线外
这样的垂线能画几条?
基本事实:过一点有且只有一条直线与这条直线垂直.(垂直性质)
说明:画一条线段或射线的垂线,就是画线段或射线所在的直线的垂线.
a
●
P
分类讨论
新知应用----典型例题
画垂线方法:
一放、二推、三画、四标.
例2:(1)在图中,
①过点A画BC的垂线,垂足为点D;
②过点B画AC的垂线,过点C画AB的垂线,垂足分别为点E、F.
B
A
C
∟
D
∟
E
∟
F
在平面图形中画垂线,类比画平行线,在网格中怎么画垂线呢?
新知应用----典型例题
网格:
(1)观察线段的放置特征(走势)
(2)利用线段走势找格点
例2:(2)在网格图中.
①用三角尺或量角器检验图中AB与BC是否互相垂直
观察图形,你能发现在方格纸中画垂线有什么简便方法吗
②运用你发现的方法,在图中过点P画PQ的垂线,并用三角尺或量角器加以检验.
●
●
P
●
M
Q
H
∴ 直线PH即为所求。
过点M作直线PQ的垂线呢?
N
∴ 直线MN即为所求。
新知应用----典型例题
例3:如图,已知直线AB、CD都经过O点,OE为射线,若∠1=35°,∠2=55°,则OE与AB的位置关系是______。
C
D
A
B
O
E
1
2
解:∵∠1=35°,∠2=55°
∴ ∠AOE=180°-∠1-∠2
= 180°-35°-55°
=90°
∴OE⊥AB (垂直定义)
垂直
N
例4:如图,直线BC与MN相交于点O,AO⊥BC,
∠BOE=∠NOE,若∠EON=20°,
求∠NOC和∠AOM的度数.
A
M
C
O
E
B
解:∵∠BOE=∠NOE,
∴∠BON=2∠EON=40°,
∴∠NOC=180°-∠BON=140°,
∠MOC=∠BON=40°.
∵AO⊥BC,
∴∠AOC=90°,
∴∠AOM=∠AOC-∠MOC=50°,
∴∠NOC=140°,∠AOM=50°.
∟
水平线
铅垂线
新知应用----垂直应用
新知应用----垂直应用
公元前十七世纪的希腊克里特岛王朝巨大的迷宫
《圣经》中hanging garden
悬园
2400年前的春秋战国时期吴王夫差就将植物种植在南京城墙上
在五代时期,后蜀皇帝更是在成都的城垣上大量的种植芙蓉使得成都直到今天都有着“蓉城”这个别称。
课堂小结
平面图形的认识
线段、射线、直线
线段的度量及画法
线段的大小比较、线段的和差
线段的中点
基本事实:两点确定一条直线;两点之间线段最短.
角的度量及作法
角的大小比较、角的和差
角的平分线
两个角的关系:余角、补角、对顶角
角
同角(等角)的余角相等;
同角(等角)的补角相等;
对顶角相等
垂
线
概念:在同一平面内,不相交的两条直线叫做平行线
平行线的表示:用“//”表示平行
找或画垂线的方法:
(1)平面内:一放、二推、三画、四标.
(2)网格内:关注线的走势
平行线
基本事实:过直线外一点有且只有一条直线与已知直线平行
概念:如果两条直线相交所成的四个角中有一个是直角,那么这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
垂线的表示:用“⊥”表示平行
基本事实:过一点有且只有一条直线与已知直线垂直
……
分类讨论思想
尝试练习
1、两条直线相交所成的四个角中,下列条件中能判定两条直线垂直的是( )
A. 有两个角相等 B.有两对角相等
C. 有三个角相等 D.有四对邻补角
C
2、点O是直线AB上的一点, OC是射线,OE平分∠AOC, OF平分∠BOC,则OE与OF的位置关系为 .
A
B
O
C
E
F
垂直
同学们,再见!
6.5 垂直(1)
苏科版八年级上册 数学
认识垂线
平面图形的认识
线段、射线、直线
角
…
概念:在同一平面内,不相交的两条直线叫做平行线
平行线的表示:用“//”表示平行
找或画平行线的方法:
(1)平面内:一放、二靠、三推、四画.
(2)网格内:关注线的走势(所在的长方形或直角三角形)
平行线
基本事实:过直线外一点有且只有一条直线与已知直线平行
b
a
相交
垂直
认识垂线
生活中我们常常会看到的场景.
生活中的许多事物留给我们有垂直的印象.
你还能说出我们生活周围遇见的哪些线互相垂直?
a
b
(普通相交)
a
b
O
A
B
D
C
(特殊相交):垂直
认识垂线
直线a、b相交于点O
2、垂直表示:两条直线a、b(AB、CD)互相垂直,
记作:a⊥b或AB⊥CD(如图),其中点O是垂足.
简单记作:a⊥b于点O,或AB⊥CD于点O.
“⊥”是书写中“垂直”的记号,
而“ ”是图形中“垂直”(直角)的标记.
(1) ∵∠AOD=90°
∴AB⊥CD
(垂直的定义)
(2) ∵AB⊥CD
∴∠AOD=90°
(垂直的定义)
垂直的判定
垂直的性质
3、几何
语言
O
1、垂直概念:如果两条直线相交所成的四个角中有一个是直角,那么这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
认识垂线
观察左侧地图:
1.图中有哪些道路与解放路垂直
2.过人民广场,并与解放路垂直的道路有几条
4.过人民广场或青年广场,能否再修一条与解放路垂直的道路
如果两条直线都与第三条直线垂直,那么这两条直线互相平行.
●
●
一放
二推
三画
画垂线的方法:
3.过青年广场,并与解放路垂直的道路呢
与已知直线垂直的直线有无数条,过一点与已知直线垂直的直线有一条.
四标
新知应用----典型例题
例1:已知直线a及一点P,过点P画直线a的垂线;
方法:一放、二推、三画、四标.
a
●
P
a
●
P
a
●
P
P在直线上
P在直线外
这样的垂线能画几条?
基本事实:过一点有且只有一条直线与这条直线垂直.(垂直性质)
说明:画一条线段或射线的垂线,就是画线段或射线所在的直线的垂线.
a
●
P
分类讨论
新知应用----典型例题
画垂线方法:
一放、二推、三画、四标.
例2:(1)在图中,
①过点A画BC的垂线,垂足为点D;
②过点B画AC的垂线,过点C画AB的垂线,垂足分别为点E、F.
B
A
C
∟
D
∟
E
∟
F
在平面图形中画垂线,类比画平行线,在网格中怎么画垂线呢?
新知应用----典型例题
网格:
(1)观察线段的放置特征(走势)
(2)利用线段走势找格点
例2:(2)在网格图中.
①用三角尺或量角器检验图中AB与BC是否互相垂直
观察图形,你能发现在方格纸中画垂线有什么简便方法吗
②运用你发现的方法,在图中过点P画PQ的垂线,并用三角尺或量角器加以检验.
●
●
P
●
M
Q
H
∴ 直线PH即为所求。
过点M作直线PQ的垂线呢?
N
∴ 直线MN即为所求。
新知应用----典型例题
例3:如图,已知直线AB、CD都经过O点,OE为射线,若∠1=35°,∠2=55°,则OE与AB的位置关系是______。
C
D
A
B
O
E
1
2
解:∵∠1=35°,∠2=55°
∴ ∠AOE=180°-∠1-∠2
= 180°-35°-55°
=90°
∴OE⊥AB (垂直定义)
垂直
N
例4:如图,直线BC与MN相交于点O,AO⊥BC,
∠BOE=∠NOE,若∠EON=20°,
求∠NOC和∠AOM的度数.
A
M
C
O
E
B
解:∵∠BOE=∠NOE,
∴∠BON=2∠EON=40°,
∴∠NOC=180°-∠BON=140°,
∠MOC=∠BON=40°.
∵AO⊥BC,
∴∠AOC=90°,
∴∠AOM=∠AOC-∠MOC=50°,
∴∠NOC=140°,∠AOM=50°.
∟
水平线
铅垂线
新知应用----垂直应用
新知应用----垂直应用
公元前十七世纪的希腊克里特岛王朝巨大的迷宫
《圣经》中hanging garden
悬园
2400年前的春秋战国时期吴王夫差就将植物种植在南京城墙上
在五代时期,后蜀皇帝更是在成都的城垣上大量的种植芙蓉使得成都直到今天都有着“蓉城”这个别称。
课堂小结
平面图形的认识
线段、射线、直线
线段的度量及画法
线段的大小比较、线段的和差
线段的中点
基本事实:两点确定一条直线;两点之间线段最短.
角的度量及作法
角的大小比较、角的和差
角的平分线
两个角的关系:余角、补角、对顶角
角
同角(等角)的余角相等;
同角(等角)的补角相等;
对顶角相等
垂
线
概念:在同一平面内,不相交的两条直线叫做平行线
平行线的表示:用“//”表示平行
找或画垂线的方法:
(1)平面内:一放、二推、三画、四标.
(2)网格内:关注线的走势
平行线
基本事实:过直线外一点有且只有一条直线与已知直线平行
概念:如果两条直线相交所成的四个角中有一个是直角,那么这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
垂线的表示:用“⊥”表示平行
基本事实:过一点有且只有一条直线与已知直线垂直
……
分类讨论思想
尝试练习
1、两条直线相交所成的四个角中,下列条件中能判定两条直线垂直的是( )
A. 有两个角相等 B.有两对角相等
C. 有三个角相等 D.有四对邻补角
C
2、点O是直线AB上的一点, OC是射线,OE平分∠AOC, OF平分∠BOC,则OE与OF的位置关系为 .
A
B
O
C
E
F
垂直
同学们,再见!
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
