6.3 数据的表示 第2课时课件(共23张PPT)2023-2024学年北师大版七年级上册数学
文档属性
| 名称 | 6.3 数据的表示 第2课时课件(共23张PPT)2023-2024学年北师大版七年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
第六章 数据的收集与整理
6.3 数据的表示
1.知道频数的意义,会求一组数据的频数;(重点)
2.会利用表格整理数据,会画频数直方图,能从频数直方图
中得到数据分布的情况.
一、学习目标
二、新课导入
我们从小学升入中学,来到新的班集体,认识了新的老师和同学,
交上新朋友;这不小胖就开始向新朋友炫耀自己的入学成绩.
我数学满分,可惜语文才考99分,拖了我后腿.
切,我听说咱们班数学最高成绩是94分.
二、新课导入
张老师听到他们的对话后,想清楚地了解他们班的整体成绩情况,
于是他拿了一份这个班的入学统计表单.
但看到统计表单有整整两页,
张老师觉得看起来很不方便.于是他
向其他老师求助.
三、概念剖析
学号 性别 身高 (厘米) 入学成绩 语文 数学 英语
1 女 167 81 88 优
2 男 162 78 85 良
3 女 165 86 90 优
4 男 160 81 99 中
5 女 165 94 86 优
6 女 167 83 75 良
7 女 165 88 94 优
8 男 166 79 98 优
9 女 159 72 65 中
10 男 169 86 97 优
11 男 168 91 96 优
12 男 158 80 93 良
13 男 160 85 89 优
14 女 159 90 84 优
15 女 162 91 89 优
学号 性别 身高 (厘米) 入学成绩 语文 数学 英语
16 女 162 83 85 优
17 女 157 86 80 优
18 女 160 92 93 优
19 男 164 83 89 优
20 女 161 75 77 良
21 男 162 86 97 优
22 男 164 91 91 优
23 女 163 87 82 优
24 男 154 82 88 优
25 男 172 68 70 中
26 男 153 88 95 优
27 男 156 80 87 优
28 男 163 82 81 优
29 男 164 78 75 良
30 女 161 89 87 优
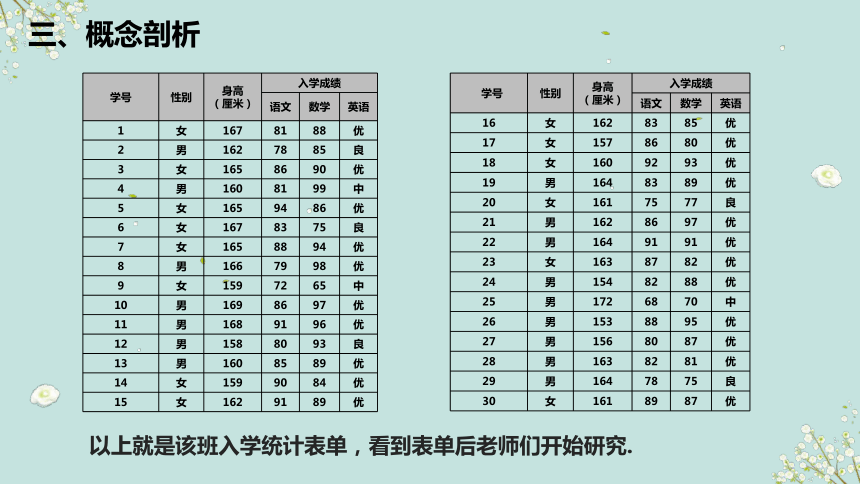
以上就是该班入学统计表单,看到表单后老师们开始研究.
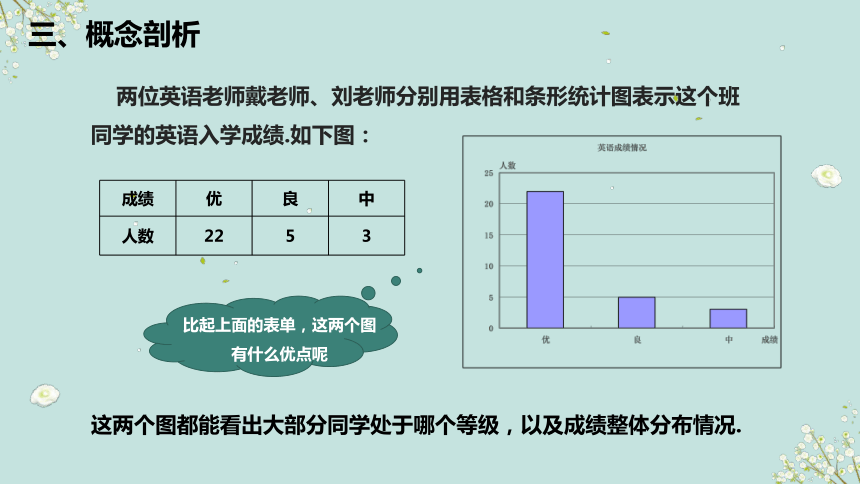
两位英语老师戴老师、刘老师分别用表格和条形统计图表示这个班
同学的英语入学成绩.如下图:
成绩 优 良 中
人数 22 5 3
这两个图都能看出大部分同学处于哪个等级,以及成绩整体分布情况.
三、概念剖析
比起上面的表单,这两个图
有什么优点呢
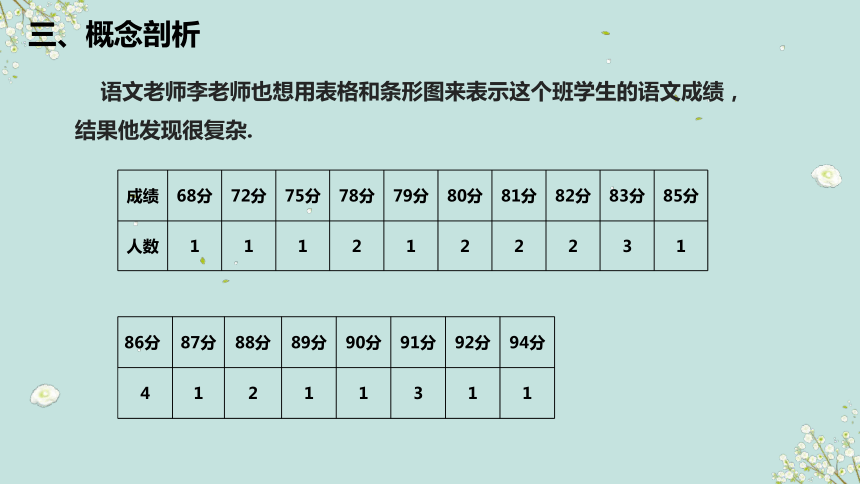
语文老师李老师也想用表格和条形图来表示这个班学生的语文成绩,
结果他发现很复杂.
成绩 68分 72分 75分 78分 79分 80分 81分 82分 83分 85分
人数 1 1 1 2 1 2 2 2 3 1
86分 87分 88分 89分 90分 91分 92分 94分
4 1 2 1 1 3 1 1
三、概念剖析
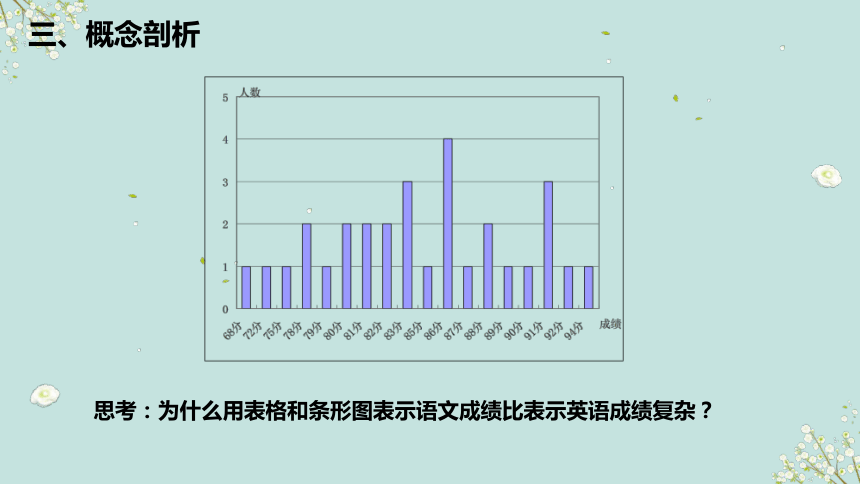
思考:为什么用表格和条形图表示语文成绩比表示英语成绩复杂?
三、概念剖析
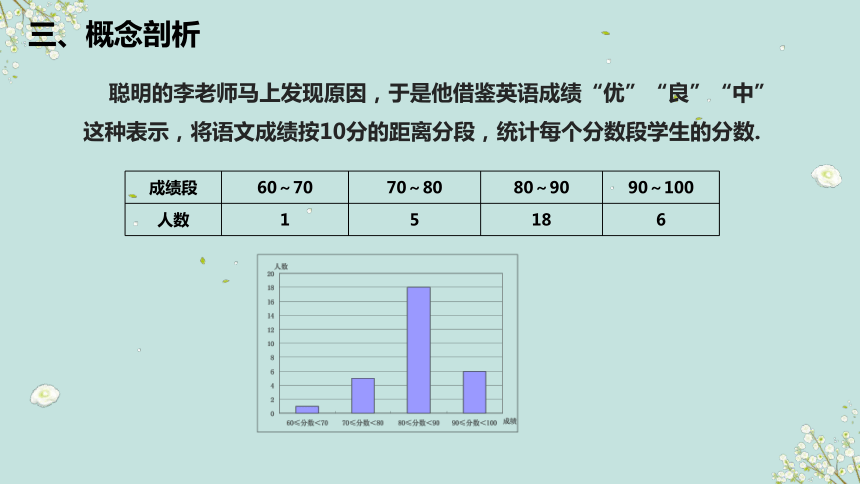
聪明的李老师马上发现原因,于是他借鉴英语成绩“优”“良”“中”
这种表示,将语文成绩按10分的距离分段,统计每个分数段学生的分数.
成绩段 60~70 70~80 80~90 90~100
人数 1 5 18 6
三、概念剖析
我们把上图的横轴略作调整,得到下图:
像这样的统计图称为频数直方图.
三、概念剖析
每个成绩段的人数为频数直方图中的频数.
三、概念剖析
频数直方图是一种特殊的条形统计图,它将统计对象的数据进行分组,画在横轴上,纵轴表示各组数据的频数.
如果样本中数据较多,数据的差距也比较大时,频数直方图能更清晰、
更直观地反映数据的整体情况.
四、典型例题
例1.某中学部分同学参加全国初中数学竞赛,并取得了优异的成绩,指
导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了如图的频数直方图(每组中含最低分数,但不含最高分数).
请回答:
4
1
0
3
2
60
70
人数(频数)
分数/分
90
80
120
100
110
5
7
6
8
(1)该中学参加本次数学竞赛的共有多少人?
分析:根据频数直方图,可以读出各分数段的人数,其和即为参加本次数学竞赛的人数.
解:4+6+8+7+5+2=32(人),
所以该中学参加本次数学竞赛的共有32人.
四、典型例题
(2)如果成绩在90分以上(含90分)的同学获奖,那么该中学参赛同学的获
奖率是多少?
分析:先计算出得分在90分以上(含90分)的人数,
结合(1)即可得出获奖率.
解:90分以上(含90分)的同学有7+5+2=14(人),
所以该中学参赛同学的获奖率是 (14÷32)×100%=43.75%.
四、典型例题
(3)图中还提供了其他信息,例如该中学没有获得满分的同学等,请再写
出两条信息.
解:该中学参赛同学的成绩均不低于60分;
成绩在80~90分(含80分,但不含90分)的人数最多;
成绩在100分以上(含100分)的同学有7人.
(答案不唯一,合理即可)
讨论:你还能获得哪些信息?
【当堂检测】
1.如图是九(1)班45名同学每周课外阅读时间的频数直方图(每组含前一个边界值,不含后一个边界值).由图可知,人数最多的一组是( )
A.2~4 h
B.4~6 h
C.6~8 h
D.8~10 h
B
2.九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是( )
A.80%
B.70%
C.92%
D.86%
【当堂检测】
C
四、典型例题
例2.为了了解本校七年级学生的身体素质情况,体育老师随机抽取了本校50名七年级学生进行一分钟跳绳次数测试,测试所得样本数据(单位:次)如下:
88 90 92 96 99 102 106 108 110 112
113 115 115 117 118 120 120 123 125 127
130 132 134 134 134 135 136 137 138 138
139 141 142 142 143 144 145 146 148 149
150 152 153 157 160 162 162 165 168 172
试着制作频数直方图表示这些数据.
四、典型例题
解:上面数据最大值为172,最小值为88,172-88=84;
取组距为20,分为5组比较合适,分组如下:
80~100,100~120,120~140,140~160,160~180;
列出频数分布表,如下:
次数 80~100 100~120 120~140 140~160 160~180
人数 5 10 16 13 6
再根据频数分布表制作频数直方图.
四、典型例题
次数 80~100 100~120 120~140 140~160 160~180
人数 5 10 16 13 6
频数直方图如下:
0
80
100
频数(人数)
次数
140
120
160
12
4
2
6
8
10
5
10
16
13
180
14
16
18
6
四、典型例题
归纳:制作频数直方图的步骤
(1)计算出数据中最大值与最小值的差;
(2)确定组距与组数:先确定组距,再根据组距求组数;
(3)列出频数分布表;
(4)由频数分布表画出频数直方图.
①在平面上作两条互相垂直的轴:横轴与纵轴;
②在横轴上划分一些相互衔接的线段,每条线段表示一组,分别标上分点数;
③在纵轴上划分刻度,并用自然数标记;
④以横轴上的每条线段为底各作一个长方形立于横轴上,设各长方形的高等于相应的频数.
3.某校七年级学生数学月考的成绩如下(每组分数含最低分,不含最高分):60~70分的60人,70~80分的45人,80~90的25人,90~100分的20人.
(1)制作频数分布表;
(2)画出频数分布直方图.
解:(1)频数分布表如下:
成绩段 60~70 70~80 80~90 90~100
人数 60 45 25 20
【当堂检测】
(2)频数直方图如下:
0
60
70
频数
成绩
90
80
100
60
20
10
30
40
50
60
45
25
20
成绩段 60~70 70~80 80~90 90~100
人数 60 45 25 20
【当堂检测】
五、课堂总结
1.频数直方图是一种以频数为纵向指标的条形统计图;
2.频数直方图中的长方形是连续排列的;
3.易于比较各组数据之间的差别,能直观显示各组数据之间具体数据
的分布情况.
第六章 数据的收集与整理
6.3 数据的表示
1.知道频数的意义,会求一组数据的频数;(重点)
2.会利用表格整理数据,会画频数直方图,能从频数直方图
中得到数据分布的情况.
一、学习目标
二、新课导入
我们从小学升入中学,来到新的班集体,认识了新的老师和同学,
交上新朋友;这不小胖就开始向新朋友炫耀自己的入学成绩.
我数学满分,可惜语文才考99分,拖了我后腿.
切,我听说咱们班数学最高成绩是94分.
二、新课导入
张老师听到他们的对话后,想清楚地了解他们班的整体成绩情况,
于是他拿了一份这个班的入学统计表单.
但看到统计表单有整整两页,
张老师觉得看起来很不方便.于是他
向其他老师求助.
三、概念剖析
学号 性别 身高 (厘米) 入学成绩 语文 数学 英语
1 女 167 81 88 优
2 男 162 78 85 良
3 女 165 86 90 优
4 男 160 81 99 中
5 女 165 94 86 优
6 女 167 83 75 良
7 女 165 88 94 优
8 男 166 79 98 优
9 女 159 72 65 中
10 男 169 86 97 优
11 男 168 91 96 优
12 男 158 80 93 良
13 男 160 85 89 优
14 女 159 90 84 优
15 女 162 91 89 优
学号 性别 身高 (厘米) 入学成绩 语文 数学 英语
16 女 162 83 85 优
17 女 157 86 80 优
18 女 160 92 93 优
19 男 164 83 89 优
20 女 161 75 77 良
21 男 162 86 97 优
22 男 164 91 91 优
23 女 163 87 82 优
24 男 154 82 88 优
25 男 172 68 70 中
26 男 153 88 95 优
27 男 156 80 87 优
28 男 163 82 81 优
29 男 164 78 75 良
30 女 161 89 87 优
以上就是该班入学统计表单,看到表单后老师们开始研究.
两位英语老师戴老师、刘老师分别用表格和条形统计图表示这个班
同学的英语入学成绩.如下图:
成绩 优 良 中
人数 22 5 3
这两个图都能看出大部分同学处于哪个等级,以及成绩整体分布情况.
三、概念剖析
比起上面的表单,这两个图
有什么优点呢
语文老师李老师也想用表格和条形图来表示这个班学生的语文成绩,
结果他发现很复杂.
成绩 68分 72分 75分 78分 79分 80分 81分 82分 83分 85分
人数 1 1 1 2 1 2 2 2 3 1
86分 87分 88分 89分 90分 91分 92分 94分
4 1 2 1 1 3 1 1
三、概念剖析
思考:为什么用表格和条形图表示语文成绩比表示英语成绩复杂?
三、概念剖析
聪明的李老师马上发现原因,于是他借鉴英语成绩“优”“良”“中”
这种表示,将语文成绩按10分的距离分段,统计每个分数段学生的分数.
成绩段 60~70 70~80 80~90 90~100
人数 1 5 18 6
三、概念剖析
我们把上图的横轴略作调整,得到下图:
像这样的统计图称为频数直方图.
三、概念剖析
每个成绩段的人数为频数直方图中的频数.
三、概念剖析
频数直方图是一种特殊的条形统计图,它将统计对象的数据进行分组,画在横轴上,纵轴表示各组数据的频数.
如果样本中数据较多,数据的差距也比较大时,频数直方图能更清晰、
更直观地反映数据的整体情况.
四、典型例题
例1.某中学部分同学参加全国初中数学竞赛,并取得了优异的成绩,指
导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了如图的频数直方图(每组中含最低分数,但不含最高分数).
请回答:
4
1
0
3
2
60
70
人数(频数)
分数/分
90
80
120
100
110
5
7
6
8
(1)该中学参加本次数学竞赛的共有多少人?
分析:根据频数直方图,可以读出各分数段的人数,其和即为参加本次数学竞赛的人数.
解:4+6+8+7+5+2=32(人),
所以该中学参加本次数学竞赛的共有32人.
四、典型例题
(2)如果成绩在90分以上(含90分)的同学获奖,那么该中学参赛同学的获
奖率是多少?
分析:先计算出得分在90分以上(含90分)的人数,
结合(1)即可得出获奖率.
解:90分以上(含90分)的同学有7+5+2=14(人),
所以该中学参赛同学的获奖率是 (14÷32)×100%=43.75%.
四、典型例题
(3)图中还提供了其他信息,例如该中学没有获得满分的同学等,请再写
出两条信息.
解:该中学参赛同学的成绩均不低于60分;
成绩在80~90分(含80分,但不含90分)的人数最多;
成绩在100分以上(含100分)的同学有7人.
(答案不唯一,合理即可)
讨论:你还能获得哪些信息?
【当堂检测】
1.如图是九(1)班45名同学每周课外阅读时间的频数直方图(每组含前一个边界值,不含后一个边界值).由图可知,人数最多的一组是( )
A.2~4 h
B.4~6 h
C.6~8 h
D.8~10 h
B
2.九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是( )
A.80%
B.70%
C.92%
D.86%
【当堂检测】
C
四、典型例题
例2.为了了解本校七年级学生的身体素质情况,体育老师随机抽取了本校50名七年级学生进行一分钟跳绳次数测试,测试所得样本数据(单位:次)如下:
88 90 92 96 99 102 106 108 110 112
113 115 115 117 118 120 120 123 125 127
130 132 134 134 134 135 136 137 138 138
139 141 142 142 143 144 145 146 148 149
150 152 153 157 160 162 162 165 168 172
试着制作频数直方图表示这些数据.
四、典型例题
解:上面数据最大值为172,最小值为88,172-88=84;
取组距为20,分为5组比较合适,分组如下:
80~100,100~120,120~140,140~160,160~180;
列出频数分布表,如下:
次数 80~100 100~120 120~140 140~160 160~180
人数 5 10 16 13 6
再根据频数分布表制作频数直方图.
四、典型例题
次数 80~100 100~120 120~140 140~160 160~180
人数 5 10 16 13 6
频数直方图如下:
0
80
100
频数(人数)
次数
140
120
160
12
4
2
6
8
10
5
10
16
13
180
14
16
18
6
四、典型例题
归纳:制作频数直方图的步骤
(1)计算出数据中最大值与最小值的差;
(2)确定组距与组数:先确定组距,再根据组距求组数;
(3)列出频数分布表;
(4)由频数分布表画出频数直方图.
①在平面上作两条互相垂直的轴:横轴与纵轴;
②在横轴上划分一些相互衔接的线段,每条线段表示一组,分别标上分点数;
③在纵轴上划分刻度,并用自然数标记;
④以横轴上的每条线段为底各作一个长方形立于横轴上,设各长方形的高等于相应的频数.
3.某校七年级学生数学月考的成绩如下(每组分数含最低分,不含最高分):60~70分的60人,70~80分的45人,80~90的25人,90~100分的20人.
(1)制作频数分布表;
(2)画出频数分布直方图.
解:(1)频数分布表如下:
成绩段 60~70 70~80 80~90 90~100
人数 60 45 25 20
【当堂检测】
(2)频数直方图如下:
0
60
70
频数
成绩
90
80
100
60
20
10
30
40
50
60
45
25
20
成绩段 60~70 70~80 80~90 90~100
人数 60 45 25 20
【当堂检测】
五、课堂总结
1.频数直方图是一种以频数为纵向指标的条形统计图;
2.频数直方图中的长方形是连续排列的;
3.易于比较各组数据之间的差别,能直观显示各组数据之间具体数据
的分布情况.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
