18.1.2平行四边形的判定课件
文档属性
| 名称 | 18.1.2平行四边形的判定课件 |  | |
| 格式 | zip | ||
| 文件大小 | 567.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-05 09:53:37 | ||
图片预览




文档简介
课件35张PPT。第十八章 平行四边形
18.2平行四边形的判定预习P81-83 了解平行四边形的判定方法 1.两组对边分别平行的四边形是平行四边形
2.两组对边分别相等的四边形是平行四边形
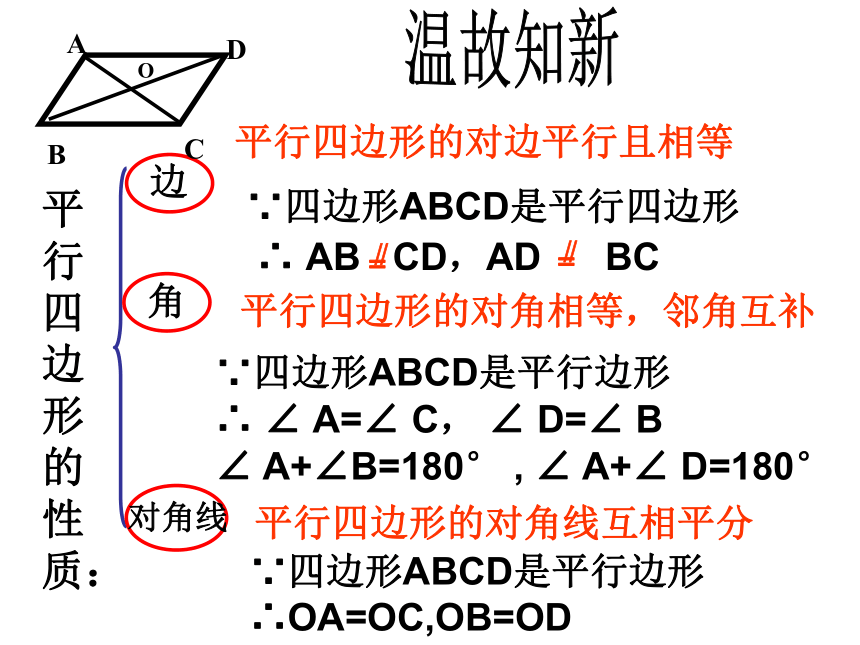
3.一组对边平行且相等的四边形是平行四边形你还记得吗? 两组对边分别平行的四边形是平行四边形平行四边形的定义忆平行四边形的对边平行且相等 平行四边形的对角线互相平分 温故知新平行四边形的性质:平行四边形的对角相等,邻角互补∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠B=180° , ∠ A+∠ D=180°∵四边形ABCD是平行边形 ∴OA=OC,OB=OD平行四边形的主要性质:
2、对角线: 平行四边形对角线互相平分1、边:a.平行四边形两组对边分别平行.b.平行四边形两组对边分别相等.两组对边分别平行的四边形是平行四边形.两组对边分别相等的四边形是平行四边形.(定义)猜 说你能分别说出他们的逆命题吗? 我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢?
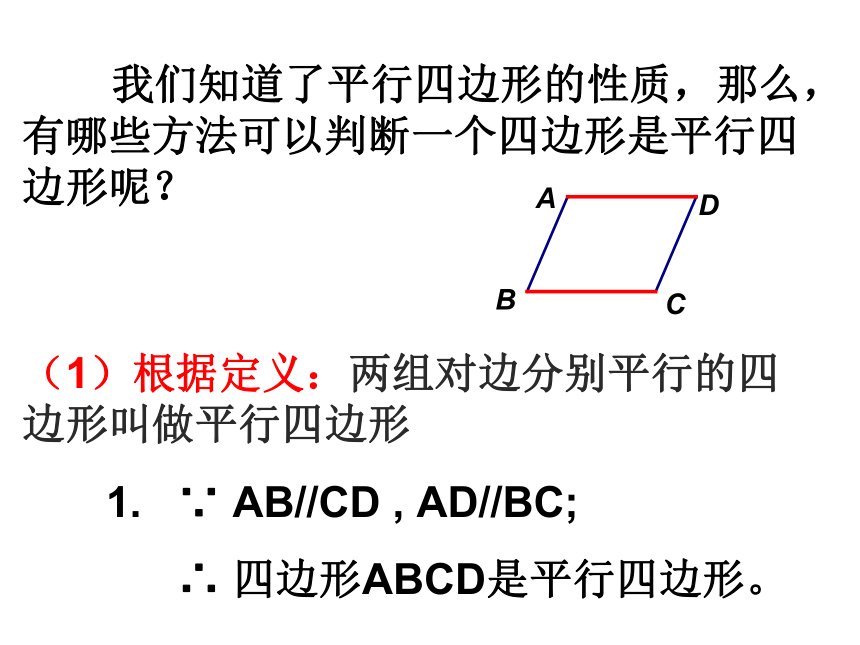
(1)根据定义:两组对边分别平行的四边形叫做平行四边形
1. ∵ AB//CD , AD//BC;
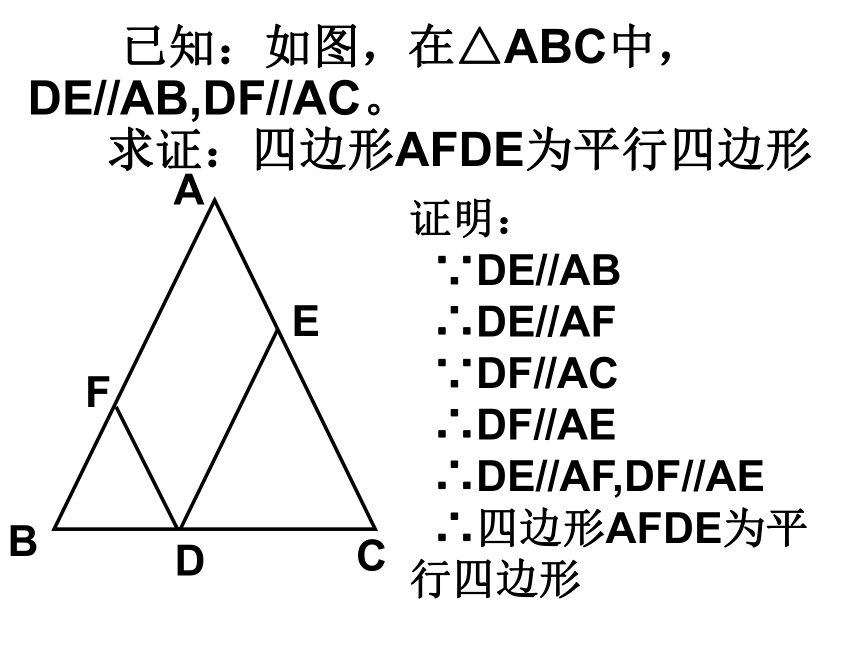
∴ 四边形ABCD是平行四边形。 一天我们班小黄同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(A,B,C为三顶点,即找出第四个顶点D)生活实际的挑战想一想方法(一)D(两组对边分别平行的四边形是平行四边形)∵AB∥CD,AD∥BC ∴四边形ABCD是平行四边形 已知:如图,在△ABC中,DE//AB,DF//AC。
求证:四边形AFDE为平行四边形证明:
∵DE//AB
∴DE//AF
∵DF//AC
∴DF//AE
∴DE//AF,DF//AE
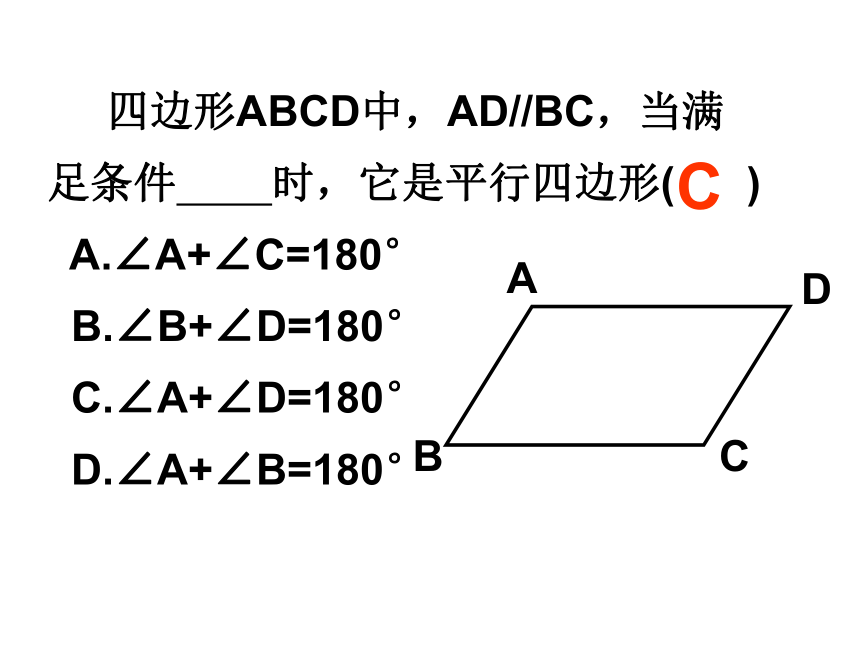
∴四边形AFDE为平行四边形 四边形ABCD中,AD//BC,当满足条件 时,它是平行四边形( )
A.∠A+∠C=180°
B.∠B+∠D=180°
C.∠A+∠D=180°
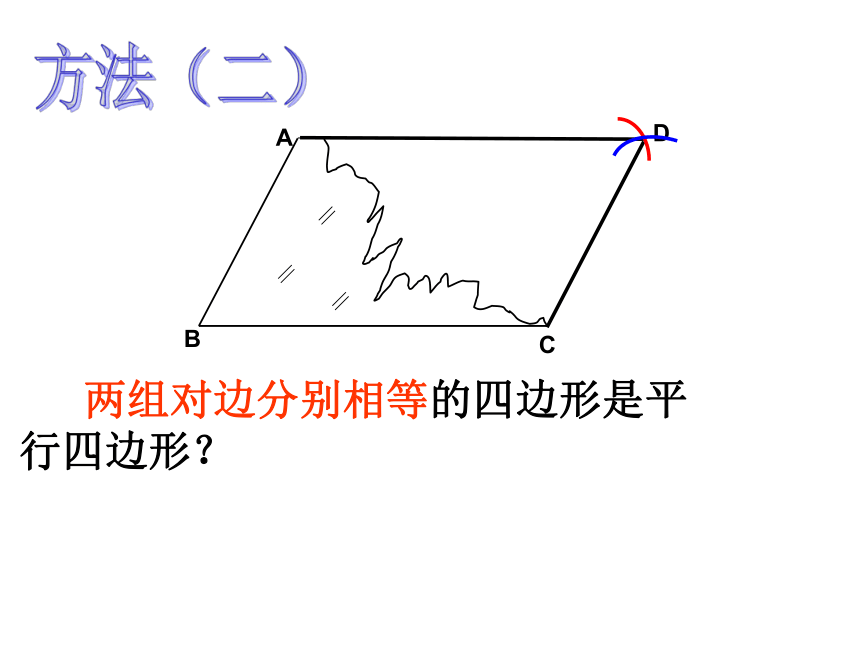
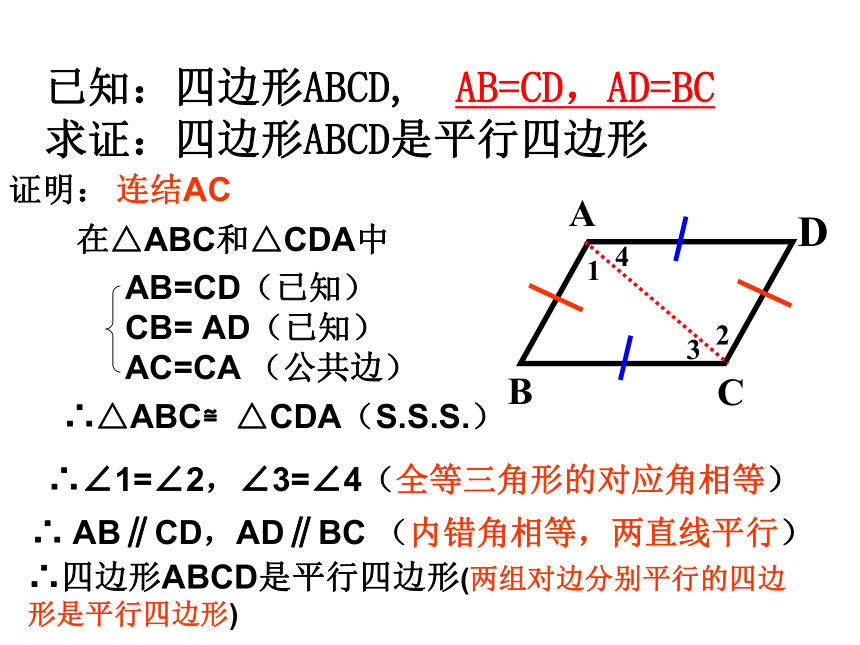
D.∠A+∠B=180°C方法(二)D 两组对边分别相等的四边形是平行四边形?已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形证明:连结AC在△ABC和△CDA中∴△ABC≌△CDA(S.S.S.)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
DBAC2134∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)两组对边分别相等的四边形是平行四边形平行四边形的判定定理1:符号语言(记一记):∵AB=CD,AD=BC∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)可求得
△ABE≌△CDF(S.A.S)
∴AE=CF
又∵AF=CE
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
如图,在□ABCD中,E、F分别是边BC和AD上的两点,且AF=CE。
求证:四边形AECF为平行四边形
已知:如图,AD⊥AC,BC⊥AC,且AB=CD. 求证:该四边形是平行四边形.证明:∵AD⊥AC, BC⊥AC ∴ AD//BC,∠BCA=∠DAC=90°
∴△ACB和△CAD是直角三角形在Rt△ACB和Rt△CAD∴Rt△ACB≌Rt△CAD(H.L.)
∴∠BAC=∠DCA
∴AB//CD∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形) AB=CD
AC=CA,┐┐已知:如图,AD⊥AC,BC⊥AC,且AB=CD. 求证:该四边形是平行四边形.证明:∵AD⊥AC, BC⊥AC ∴ ∠BCA=∠DAC=90°
∴△ACB和△CAD是直角三角形在Rt△ACB和Rt△CAD∴Rt△ACB≌Rt△CAD(H.L.)
∴BC=DA
∵AB=CD∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形) AB=CD
AC=CA,┐┐ 已知:如图,AD⊥AC,BC⊥AC,且AB=CD. 求证:AB∥CD.证明:∵AD⊥AC, BC⊥AC∴AD∥BC, ∠BCA=∠DAC=90°
∴△ACB和△CAD是直角三角形在Rt△ACB和Rt△CAD∴Rt△ACB≌Rt△CAD(H.L.)
∴AD=BC∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)∴AB∥CD(平行四边形的两组对边分别平行) AB=CD
AC=CA,┐┐ 已知,如图,E、F、G、H分别是平行四边形ABCD的边AB、BC、CD、DA上的点,且AE=CG,BF=DH。 求证:四边形EFGH是平行四边形。 1.两组对边分别平行的四边形是平行四边形(定义) 2.两组对边分别相等的四边形是平行四边形平行四边形的判定方法:方法(三)DAD//BC,
AD=BC求证:四边形ABCD是平行四边形。 证明:连接AC ∵AD∥BC ∴∠1=∠2…… ∴ΔABC≌ΔCDA(S.A.S)∴∠BAC=∠DCA∴AB∥CD ∴四边形ABCD是平行四边形 已知:在四边形ABCD中, AD BC。(两组对边分别平行的四边形是平行四边形)你还有其他证法吗?12求证:四边形ABCD是平行四边形。 证明:连接AC ∵AD∥BC ∴∠1=∠2…… ∴ΔABC≌ΔCDA(S.A.S)∴AB=CD
∵AD=BC∴四边形ABCD是平行四边形 已知:在四边形ABCD中, AD BC。(两组对边分别相等的四边形是平行四边形)12一组对边平行且相等的四边形是平行四边形平行四边形的判定定理2:(P82)符号语言:∵AB//CD , AB=CD ∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)“平行且相等”常用符号“ ”来表示AB∥CD且AB=CD,记作“AB CD”读作:“AB平行且等于CD” 一组对边平行,另一组对边相等的四边形是平行四边形命 题:CBDACBDA是假命题 如图,在□ABCD中,E、F分别是边BC和AD上的两点,且AF=CE。
求证:四边形AECF为平行四边形
证明:∵ 四边形ABCD是平行四边形
∴ AD∥BC
即 AF∥CE
又∵ AF=CE
∴ 四边形AECF是平行四边形
(一组对边平行且相等的四边形是平行四边形)
如图,在平行四边形ABCD中,已知M和N分别是AB和DC上的中点, 求证:四边形BNDM是平行四边形。(P85 练习第3题)如图,在平行四边形ABCD中,已知M和N分别是AB和DC上的中点, 求证:四边形BNDM是平行四边形。证明:∵四边形ABCD是平行四边形,∴AB∥CD (平行四边形的两组对边分别平行) AB=CD(平行四边形的对边相等)∵M、N分别是AB、CD的中点,∴四边形BNDM是平行四边形(一组对边 平行且相等的四边形是平行四边形)。∴BM∥DN ∴BM=DN 1.两组对边分别平行的四边形是平行四边形(定义) 2.两组对边分别相等的四边形是平行四边形平行四边形的判定方法: 3.一组对边平行且相等的四边形是平行四边形得 若AB∥CD,补充条件_____, 使四边形ABCD为平行四边形。
如图,四边形ABCD中
若AD=CB,补充条件_____,使四边形ABCD为平行四边形。练填 空:AD∥CB
或AB=CD
AD∥CB
或AB=CD 如图,下列四组条件中,不能判定四边形ABCD是平行四边形的是( )
A. AB=DC,AD=BC
B. AB//DC,AD//BC
C. AB//DC,AD=BC
D. AB//DC,AB=DCC 四边形ABCD中,已知AB=7cm,BC=5cm,CD=7cm,当AD= 时,四边形ABCD是平行四边形。7575cm 已知一个四边形的四条边长顺次为a、b、c、d,且a2+b2+c2+d2=2(bd+ac),
则这个四边形是?
(积极思考 必会题型哟)解:∵a2+b2+c2+d2=2(bd+ac)
∴ a2+b2+c2+d2-2bd-2ac=0
∴ a2-2ac+c2+b2-2bd+d2=0
∴ (a-c)2+(b-d)2=0
∴a=c,b=d
∴这个四边形为平行四边形
(两组对边分别相等的四边形是平行四边形) 已知一个凸四边形的四条边长顺次为a、b、c、d,且a2+ab-ac-bc=0,b2+bc-bd-cd=0,则这个四边形是? ∵a2+ab-ac-bc=0
∴ a(a+b)-c(a+b)=0
∴ (a-c)(a+b)=0
∵a、b、c、d是边长
∴a+b>0,a-c=0
∴a=c ∵b2+bc-bd-cd=0
∴b(b+c)-d(b+c)=0
∴ (b-d)(b+c)=0
∵a、b、c、d是边长
∴b+c>0,b-d=0
∴b=d 在下面的格点图中,以格点为顶点,你能画出多少个平行四边形? (P85 练习第1题) 在□ABCD中,AE=CF,M、N分别是DE、BF的中点,四边形ENFM是平行四边形吗?
18.2平行四边形的判定预习P81-83 了解平行四边形的判定方法 1.两组对边分别平行的四边形是平行四边形
2.两组对边分别相等的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形你还记得吗? 两组对边分别平行的四边形是平行四边形平行四边形的定义忆平行四边形的对边平行且相等 平行四边形的对角线互相平分 温故知新平行四边形的性质:平行四边形的对角相等,邻角互补∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠B=180° , ∠ A+∠ D=180°∵四边形ABCD是平行边形 ∴OA=OC,OB=OD平行四边形的主要性质:
2、对角线: 平行四边形对角线互相平分1、边:a.平行四边形两组对边分别平行.b.平行四边形两组对边分别相等.两组对边分别平行的四边形是平行四边形.两组对边分别相等的四边形是平行四边形.(定义)猜 说你能分别说出他们的逆命题吗? 我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢?
(1)根据定义:两组对边分别平行的四边形叫做平行四边形
1. ∵ AB//CD , AD//BC;
∴ 四边形ABCD是平行四边形。 一天我们班小黄同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(A,B,C为三顶点,即找出第四个顶点D)生活实际的挑战想一想方法(一)D(两组对边分别平行的四边形是平行四边形)∵AB∥CD,AD∥BC ∴四边形ABCD是平行四边形 已知:如图,在△ABC中,DE//AB,DF//AC。
求证:四边形AFDE为平行四边形证明:
∵DE//AB
∴DE//AF
∵DF//AC
∴DF//AE
∴DE//AF,DF//AE
∴四边形AFDE为平行四边形 四边形ABCD中,AD//BC,当满足条件 时,它是平行四边形( )
A.∠A+∠C=180°
B.∠B+∠D=180°
C.∠A+∠D=180°
D.∠A+∠B=180°C方法(二)D 两组对边分别相等的四边形是平行四边形?已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形证明:连结AC在△ABC和△CDA中∴△ABC≌△CDA(S.S.S.)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
DBAC2134∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)两组对边分别相等的四边形是平行四边形平行四边形的判定定理1:符号语言(记一记):∵AB=CD,AD=BC∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)可求得
△ABE≌△CDF(S.A.S)
∴AE=CF
又∵AF=CE
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
如图,在□ABCD中,E、F分别是边BC和AD上的两点,且AF=CE。
求证:四边形AECF为平行四边形
已知:如图,AD⊥AC,BC⊥AC,且AB=CD. 求证:该四边形是平行四边形.证明:∵AD⊥AC, BC⊥AC ∴ AD//BC,∠BCA=∠DAC=90°
∴△ACB和△CAD是直角三角形在Rt△ACB和Rt△CAD∴Rt△ACB≌Rt△CAD(H.L.)
∴∠BAC=∠DCA
∴AB//CD∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形) AB=CD
AC=CA,┐┐已知:如图,AD⊥AC,BC⊥AC,且AB=CD. 求证:该四边形是平行四边形.证明:∵AD⊥AC, BC⊥AC ∴ ∠BCA=∠DAC=90°
∴△ACB和△CAD是直角三角形在Rt△ACB和Rt△CAD∴Rt△ACB≌Rt△CAD(H.L.)
∴BC=DA
∵AB=CD∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形) AB=CD
AC=CA,┐┐ 已知:如图,AD⊥AC,BC⊥AC,且AB=CD. 求证:AB∥CD.证明:∵AD⊥AC, BC⊥AC∴AD∥BC, ∠BCA=∠DAC=90°
∴△ACB和△CAD是直角三角形在Rt△ACB和Rt△CAD∴Rt△ACB≌Rt△CAD(H.L.)
∴AD=BC∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)∴AB∥CD(平行四边形的两组对边分别平行) AB=CD
AC=CA,┐┐ 已知,如图,E、F、G、H分别是平行四边形ABCD的边AB、BC、CD、DA上的点,且AE=CG,BF=DH。 求证:四边形EFGH是平行四边形。 1.两组对边分别平行的四边形是平行四边形(定义) 2.两组对边分别相等的四边形是平行四边形平行四边形的判定方法:方法(三)DAD//BC,
AD=BC求证:四边形ABCD是平行四边形。 证明:连接AC ∵AD∥BC ∴∠1=∠2…… ∴ΔABC≌ΔCDA(S.A.S)∴∠BAC=∠DCA∴AB∥CD ∴四边形ABCD是平行四边形 已知:在四边形ABCD中, AD BC。(两组对边分别平行的四边形是平行四边形)你还有其他证法吗?12求证:四边形ABCD是平行四边形。 证明:连接AC ∵AD∥BC ∴∠1=∠2…… ∴ΔABC≌ΔCDA(S.A.S)∴AB=CD
∵AD=BC∴四边形ABCD是平行四边形 已知:在四边形ABCD中, AD BC。(两组对边分别相等的四边形是平行四边形)12一组对边平行且相等的四边形是平行四边形平行四边形的判定定理2:(P82)符号语言:∵AB//CD , AB=CD ∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)“平行且相等”常用符号“ ”来表示AB∥CD且AB=CD,记作“AB CD”读作:“AB平行且等于CD” 一组对边平行,另一组对边相等的四边形是平行四边形命 题:CBDACBDA是假命题 如图,在□ABCD中,E、F分别是边BC和AD上的两点,且AF=CE。
求证:四边形AECF为平行四边形
证明:∵ 四边形ABCD是平行四边形
∴ AD∥BC
即 AF∥CE
又∵ AF=CE
∴ 四边形AECF是平行四边形
(一组对边平行且相等的四边形是平行四边形)
如图,在平行四边形ABCD中,已知M和N分别是AB和DC上的中点, 求证:四边形BNDM是平行四边形。(P85 练习第3题)如图,在平行四边形ABCD中,已知M和N分别是AB和DC上的中点, 求证:四边形BNDM是平行四边形。证明:∵四边形ABCD是平行四边形,∴AB∥CD (平行四边形的两组对边分别平行) AB=CD(平行四边形的对边相等)∵M、N分别是AB、CD的中点,∴四边形BNDM是平行四边形(一组对边 平行且相等的四边形是平行四边形)。∴BM∥DN ∴BM=DN 1.两组对边分别平行的四边形是平行四边形(定义) 2.两组对边分别相等的四边形是平行四边形平行四边形的判定方法: 3.一组对边平行且相等的四边形是平行四边形得 若AB∥CD,补充条件_____, 使四边形ABCD为平行四边形。
如图,四边形ABCD中
若AD=CB,补充条件_____,使四边形ABCD为平行四边形。练填 空:AD∥CB
或AB=CD
AD∥CB
或AB=CD 如图,下列四组条件中,不能判定四边形ABCD是平行四边形的是( )
A. AB=DC,AD=BC
B. AB//DC,AD//BC
C. AB//DC,AD=BC
D. AB//DC,AB=DCC 四边形ABCD中,已知AB=7cm,BC=5cm,CD=7cm,当AD= 时,四边形ABCD是平行四边形。7575cm 已知一个四边形的四条边长顺次为a、b、c、d,且a2+b2+c2+d2=2(bd+ac),
则这个四边形是?
(积极思考 必会题型哟)解:∵a2+b2+c2+d2=2(bd+ac)
∴ a2+b2+c2+d2-2bd-2ac=0
∴ a2-2ac+c2+b2-2bd+d2=0
∴ (a-c)2+(b-d)2=0
∴a=c,b=d
∴这个四边形为平行四边形
(两组对边分别相等的四边形是平行四边形) 已知一个凸四边形的四条边长顺次为a、b、c、d,且a2+ab-ac-bc=0,b2+bc-bd-cd=0,则这个四边形是? ∵a2+ab-ac-bc=0
∴ a(a+b)-c(a+b)=0
∴ (a-c)(a+b)=0
∵a、b、c、d是边长
∴a+b>0,a-c=0
∴a=c ∵b2+bc-bd-cd=0
∴b(b+c)-d(b+c)=0
∴ (b-d)(b+c)=0
∵a、b、c、d是边长
∴b+c>0,b-d=0
∴b=d 在下面的格点图中,以格点为顶点,你能画出多少个平行四边形? (P85 练习第1题) 在□ABCD中,AE=CF,M、N分别是DE、BF的中点,四边形ENFM是平行四边形吗?
