《1平均数》课件(共24张PPT)2023-2024学年北师大版数学八年级上册
文档属性
| 名称 | 《1平均数》课件(共24张PPT)2023-2024学年北师大版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-11 19:53:53 | ||
图片预览






文档简介
(共24张PPT)
1 平均数第一课时
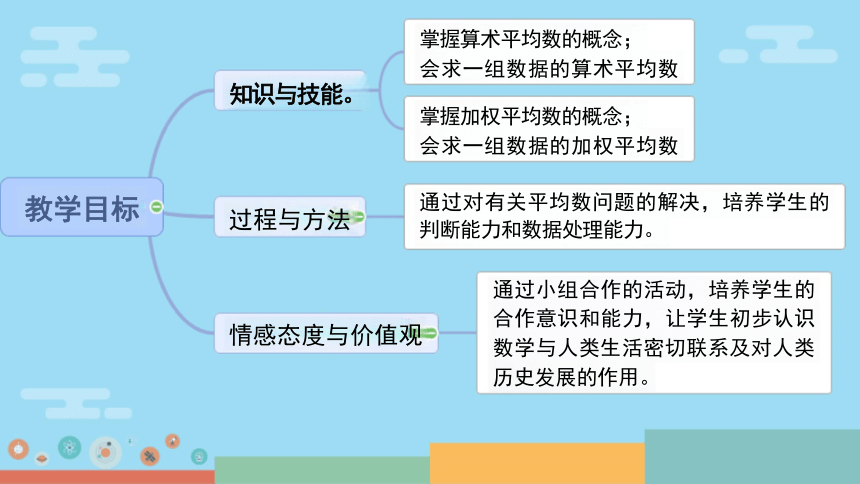
通过小组合作的活动,培养学生的
合作意识和能力,让学生初步认识 数学与人类生活密切联系及对人类 历史发展的作用。
掌握算术平均数的概念;
会求一组数据的算术平均数
掌握加权平均数的概念;
会求一组数据的加权平均数
通过对有关平均数问题的解决,培养学生的
判断能力和数据处理能力。
情感态度与价值观
知识与技能。
教学目标
过程与方法
1: 情境引入
我寻生活中的平均数
1、 各类比赛(歌咏赛、跳水比赛、课堂竞赛)
2、成绩计算
3、房地产行业:某楼盘均价4500元/平米
4、体育行业:跳水比赛、篮球比赛、体操比赛等。
1: 情境引入
篮球运动是大家喜欢的一种运动项目,尤其男生们更倍爱有加.
我们都看过篮球比赛,请同学们思考:
(1)影响比赛成绩的因素有哪些
心理、技术、配合、身高、年龄等因素
(2)如何衡量两个球队队员的身高和年龄 怎样理
解“哪支球队队员的身高更高”、“哪支球队的队员更年 轻 ”要比较两个球队队员的身高和年龄,需要收集哪
些数据呢
广东队 序号 身高/cm
年龄/岁
1 211
33
2 206
31
3 194
24
4 206
31
5 190
22
6 183
20
7 201
21
8 201
26
9 213
31
10 197
25
11 196
31
12 198
34
辽宁队 序号 身高/cm
年龄/岁
1 192
27
2 215
33
3 185
25
4 206
30
5 194
29
6 205
30
7 186
24
8 199
25
9 206
27
10 190
23
11 196
25
12 196
30
13 196
33
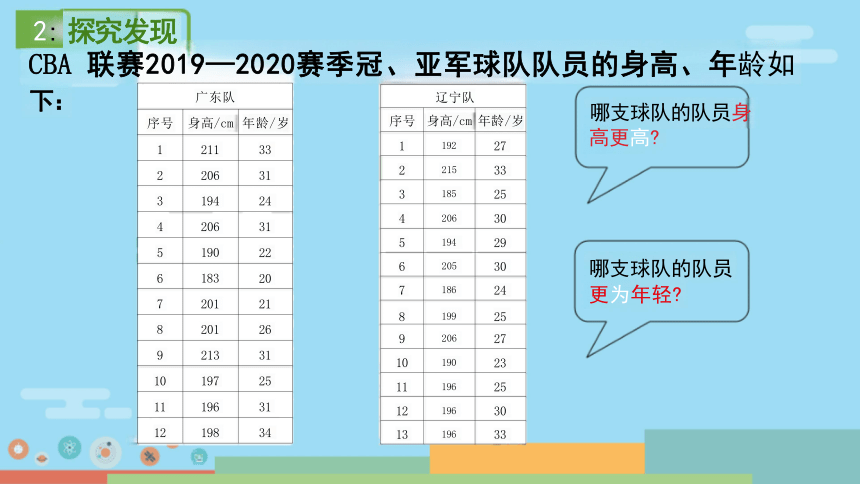
2: 探究发现
CBA 联赛2019—2020赛季冠、亚军球队队员的身高、年龄如
哪支球队的队员身
高更高
哪支球队的队员
更为年轻
下:
广东队 序号 身高/cm
年龄/岁
1 211
33
2 206
31
3 194
24
4 206
31
5 190
22
6 183
20
7 201
21
8 201
26
9 213
31
10 197
25
11 196
31
12 198
34
辽宁队 序号 身高/cm
年龄/岁
1 192
27
2 215
33
3 185
25
4 206
30
5 194
29
6 205
30
7 186
24
8 199
25
9 206
27
10 190
23
11 196
25
12 196
30
13 196
33
两支球队中,哪支
球队队员的身高更
高 哪支球队队员更
为年轻 你是怎样判 断的
2:探究发现
CBA联赛2019—2020赛季冠、亚军球队队员的身高、年龄如下:
2 : 探究发现
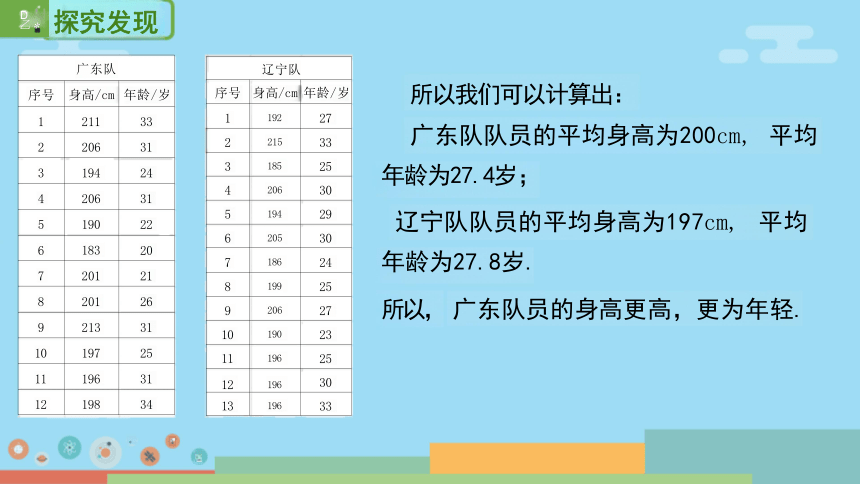
日常生活中,我们常用平均数表示一组数据的“平均水平”.
一般地,对于n个数x ,x ,…,Xn, 我们把
叫做这n个数的算术平均数,简称平均数,记做 x (读作x拔).
Y
所以我们可以计算出:
广东队队员的平均身高为200cm, 平均
年龄为27.4岁;
辽宁队队员的平均身高为197cm, 平均
年龄为27.8岁.
所以, 广东队员的身高更高,更为年轻.
广东队 序号 身高/cm
年龄/岁
1 211
33
2 206
31
3 194
24
4 206
31
5 190
22
6 183
20
7 201
21
8 201
26
9 213
31
10 197
25
11 196
31
12 198
34
辽宁队 序号 身高/cm
年龄/岁
1 192
27
2 215
33
3 185
25
4 206
30
5 194
29
6 205
30
7 186
24
8 199
25
9 206
27
10 190
23
11 196
25
12 196
30
13 196
33
* 探究发现
乙
D
*
=(23×1+24×1+25×3+27×2+29×1+30×3+33×2)÷(1+1+3+2+1+3+2)
=27.8(岁)
你能说说小明这样做的道理吗
小明的做法还是根据算术平均数的公式进行计算的,只是在求相同加
数的和时用了乘法,因此这是一种求算术平均数的简便方法.
年龄/岁 23 24 25 27 29 30
33
相应队员数 1 1 3 2 1 3
2
想一想:小明是这样计算辽宁队员的平均年龄的:
探究发现
平均年龄
跟踪训练
1 . — 组数据7,8,10,12,13的平均数是 (C)
A.7 B.9 C.10 D.12
2.若一组数据3,4,5,x,6,7 的平均数是5,则x的值是 ( D )
A.4 B.5 C.6 D.7
3.某班有50名学生,平均身高为166cm, 其中20名女生的平均身高为163cm, 则30名男生的平均
身高为1 68 cm。 (包头中考题)
变式训练:有m 个数据的平均值是x,n 个数据的平均值是y, 则m+n 个数的平均值
(2019浙江省中考题)
2 : 探究发现
例1 某广告公司欲招聘广告策划人员一名,对A、B、C 三名候选人进行了
三项素质测试.他们的各项测试成绩如下表所示:
(1)如果根据三项测试的平均成绩确
定录用人选,那么谁将被录用
解: (1) A 的平均成绩为(72+50+88)÷3=70分.
B的平均成绩为(85+74+45)÷3=68分. C的平均成绩为(67+70+67)÷3=68分. 由于70>68,故A将被录用.
测试项 目 测试成绩
A B
C
创 新 72 85
67
综合知 识 50 74
70
语 言 88 45
67
Y
(2)根据实际需要,公司将创新、综合知识和
语言三项测试得分按4:3:1的比例确定各人的 测试成绩,此时谁将被录用
解: (2) A 的测试成绩为:
(72×4+50×3+88×1)÷(4+3+1)=65.75分.
B 的测试成绩为
(85×4+74×3+45×1)÷(4+3+1)=75.875分.
C的测试成绩为:
(67×4+70×3+67×1)÷(4+3+1)=68.125分.
因此B 将被录用.
探究发现
例1 某广告公司欲招聘广告策划人员一名,对A、B、C 三名候选人进行了
三项素质测试.他们的各项测试成绩如下表所示:
测试项 目 测试成绩
A B
C
创 新 72 85
67
综合知 识 50 74
70
语 言 88 45
67
Y
(1)如果根据三项测试的平均成绩确定录用人
选,那么谁将被录用
(2)根据实际需要,公司将创新、综合知识和
语言三项测试得分按4:3:1的比例确定各人的 测试成绩,此时谁将被录用
第 ( 1 ) (2)问中录用的人不一样说明了什么
探究发现
例1 某广告公司欲招聘广告策划人员一名,对A、B、C 三名候选人进行了
三项素质测试.他们的各项测试成绩如下表所示:
测试项 测试成绩
A B
C
创 新 72 85
67
综合知 识 50 74
70
语 言 88 45
67
Y
Z: 探究发现
由于测试的每一项的重要性不同,所以所占的比份也不同,计算出的平均数就不同,
因此重要性的差异对结果的影响是很大的.
实际问题中, 一组数据里的各个数据的“重要程度”未必相同,因而在计算这组数据的平
均数时,往往给每个数据一个“权”.
如例1中4,3,1分别是创新、综合知识、语言三项测试成绩的权,
为 A的三项测试成结的如权平均数
H
而
Y
跟踪训练
1、小明和小颖本学期的数学平时成绩、期中成绩、期末成绩分别如
下: (单位:分)
小明:平时85,期中90,期末92.
小颖:平时90,期中83,期末84.
假如学期总评分按平时成绩、期中成绩、期末成绩各占
2,4,6的比例来计算,那么小明和小颖的总评分谁更高 (结果
留到个 ) 85×2+90×4+92×6 ≈ 90 (分)
2+4+6 权 以比的形式出现
小颖的总评分=9 ×2 4+84×6≈85 (分)
答:小明的总评分高。
4
3
一班 二班 三班
四班
平均分数 81 90 85
80
班级人数 55 40 45
60
81×55+90×40+85×45+80×60
55+40+45+60
2. 八年级数学期末考试成绩如下:(易错题)
求八年级期末考试的数学平均分数
八年级期末考试的数学平均分数=
权以整数的形式出现
=83.4(分)
Y
3.学校进行广播操比赛,如图是20位评委给某班的评分情况统计
图,则该班的平均得分是 0)1.1 刀 。
人数/人
10 8 7
权以整数的形式出现
5
5
评分/分
10
8
9
4.某校在期末考核学生的体育成绩时,将早锻炼及体育课外活动表现
占成绩的20%,体育理论测试占30%,体育技能测试占50%.小颖的上
述成绩分别为92分、80分、84分,则小颖这学期的体育成绩是多少
解 :小颖这学期的体育成绩是
92×20%+80×30%+84×50%=84.4(分)
答:小颖这学期的体育成绩是84.4分.
权以百分比的形式出现
测试 项目 测试成绩/分 甲 乙
丙
笔试 75 80
90
面试 - 70
68
5. 综合能力题
某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试
和面试两项测试,三人的测试成绩如下表所示:
甲
P
丙
图1
*
又根据录用程序,组织200名职工利用投票推荐的方式对三人进行民主评议(没有
弃权票,每名职工只能推荐1人,三人得票率如图1所示,每得一票记作1分。
(1)请算出三人的民主评议得分。
(2)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确
到0.01)
(3)根据实际需要,单位将笔试、面试、民主评议三项测试得分按4:3:3的
比例确定个人成绩,那么谁将被录用
答案: (1)甲的民主评议得分=200×25%=50(分)
乙的民主评议得分=200×40%=80(分)
丙的民主评议得分=200×35%=70(分)
Y
77.4>77>72.9,所以候选人丙将被录用。
(2)甲的平均成绩=
乙的平均成绩= 丙的平均成绩=
因为76.67>76>72.67,所以候选人乙将被录用。
〇 厂甲的个人成绩=75×4493+350× =72. 9 (J 刀)
75+93+50
3
80+70+80
90+68+7(
Z18
三 二 - ≈72.67(分)
) 状
-3
1
( ) )
7667
0.0/
- 3
2Z(
则(1)数据4x ,4x ,4x ,4x ,4x 的平均数为
(2)4x -2,4x -2,4x -2,4x -2,4x -2 的平均数为 o
(3)4x +2,4x +2,4x +2,4x +2,4x +2 的平均数为
知识拓展
1.已知数据x ,x ,x ,X ,x 的平均数为a,
课堂小结 通过这节课的学习,你有什么样的收获
理解概念
=(×+x+…+x)
计算公式
概念
整数
比
百分比
算术平均数
权的表现形式
加权平均数
x= i"+*2" +…+" "r
H' +Wz+·+N
平均数
公式
出题小达人
以小组形式每组出一道关于算术平均数和一道
关于加权平均数的题。
1 平均数第一课时
通过小组合作的活动,培养学生的
合作意识和能力,让学生初步认识 数学与人类生活密切联系及对人类 历史发展的作用。
掌握算术平均数的概念;
会求一组数据的算术平均数
掌握加权平均数的概念;
会求一组数据的加权平均数
通过对有关平均数问题的解决,培养学生的
判断能力和数据处理能力。
情感态度与价值观
知识与技能。
教学目标
过程与方法
1: 情境引入
我寻生活中的平均数
1、 各类比赛(歌咏赛、跳水比赛、课堂竞赛)
2、成绩计算
3、房地产行业:某楼盘均价4500元/平米
4、体育行业:跳水比赛、篮球比赛、体操比赛等。
1: 情境引入
篮球运动是大家喜欢的一种运动项目,尤其男生们更倍爱有加.
我们都看过篮球比赛,请同学们思考:
(1)影响比赛成绩的因素有哪些
心理、技术、配合、身高、年龄等因素
(2)如何衡量两个球队队员的身高和年龄 怎样理
解“哪支球队队员的身高更高”、“哪支球队的队员更年 轻 ”要比较两个球队队员的身高和年龄,需要收集哪
些数据呢
广东队 序号 身高/cm
年龄/岁
1 211
33
2 206
31
3 194
24
4 206
31
5 190
22
6 183
20
7 201
21
8 201
26
9 213
31
10 197
25
11 196
31
12 198
34
辽宁队 序号 身高/cm
年龄/岁
1 192
27
2 215
33
3 185
25
4 206
30
5 194
29
6 205
30
7 186
24
8 199
25
9 206
27
10 190
23
11 196
25
12 196
30
13 196
33
2: 探究发现
CBA 联赛2019—2020赛季冠、亚军球队队员的身高、年龄如
哪支球队的队员身
高更高
哪支球队的队员
更为年轻
下:
广东队 序号 身高/cm
年龄/岁
1 211
33
2 206
31
3 194
24
4 206
31
5 190
22
6 183
20
7 201
21
8 201
26
9 213
31
10 197
25
11 196
31
12 198
34
辽宁队 序号 身高/cm
年龄/岁
1 192
27
2 215
33
3 185
25
4 206
30
5 194
29
6 205
30
7 186
24
8 199
25
9 206
27
10 190
23
11 196
25
12 196
30
13 196
33
两支球队中,哪支
球队队员的身高更
高 哪支球队队员更
为年轻 你是怎样判 断的
2:探究发现
CBA联赛2019—2020赛季冠、亚军球队队员的身高、年龄如下:
2 : 探究发现
日常生活中,我们常用平均数表示一组数据的“平均水平”.
一般地,对于n个数x ,x ,…,Xn, 我们把
叫做这n个数的算术平均数,简称平均数,记做 x (读作x拔).
Y
所以我们可以计算出:
广东队队员的平均身高为200cm, 平均
年龄为27.4岁;
辽宁队队员的平均身高为197cm, 平均
年龄为27.8岁.
所以, 广东队员的身高更高,更为年轻.
广东队 序号 身高/cm
年龄/岁
1 211
33
2 206
31
3 194
24
4 206
31
5 190
22
6 183
20
7 201
21
8 201
26
9 213
31
10 197
25
11 196
31
12 198
34
辽宁队 序号 身高/cm
年龄/岁
1 192
27
2 215
33
3 185
25
4 206
30
5 194
29
6 205
30
7 186
24
8 199
25
9 206
27
10 190
23
11 196
25
12 196
30
13 196
33
* 探究发现
乙
D
*
=(23×1+24×1+25×3+27×2+29×1+30×3+33×2)÷(1+1+3+2+1+3+2)
=27.8(岁)
你能说说小明这样做的道理吗
小明的做法还是根据算术平均数的公式进行计算的,只是在求相同加
数的和时用了乘法,因此这是一种求算术平均数的简便方法.
年龄/岁 23 24 25 27 29 30
33
相应队员数 1 1 3 2 1 3
2
想一想:小明是这样计算辽宁队员的平均年龄的:
探究发现
平均年龄
跟踪训练
1 . — 组数据7,8,10,12,13的平均数是 (C)
A.7 B.9 C.10 D.12
2.若一组数据3,4,5,x,6,7 的平均数是5,则x的值是 ( D )
A.4 B.5 C.6 D.7
3.某班有50名学生,平均身高为166cm, 其中20名女生的平均身高为163cm, 则30名男生的平均
身高为1 68 cm。 (包头中考题)
变式训练:有m 个数据的平均值是x,n 个数据的平均值是y, 则m+n 个数的平均值
(2019浙江省中考题)
2 : 探究发现
例1 某广告公司欲招聘广告策划人员一名,对A、B、C 三名候选人进行了
三项素质测试.他们的各项测试成绩如下表所示:
(1)如果根据三项测试的平均成绩确
定录用人选,那么谁将被录用
解: (1) A 的平均成绩为(72+50+88)÷3=70分.
B的平均成绩为(85+74+45)÷3=68分. C的平均成绩为(67+70+67)÷3=68分. 由于70>68,故A将被录用.
测试项 目 测试成绩
A B
C
创 新 72 85
67
综合知 识 50 74
70
语 言 88 45
67
Y
(2)根据实际需要,公司将创新、综合知识和
语言三项测试得分按4:3:1的比例确定各人的 测试成绩,此时谁将被录用
解: (2) A 的测试成绩为:
(72×4+50×3+88×1)÷(4+3+1)=65.75分.
B 的测试成绩为
(85×4+74×3+45×1)÷(4+3+1)=75.875分.
C的测试成绩为:
(67×4+70×3+67×1)÷(4+3+1)=68.125分.
因此B 将被录用.
探究发现
例1 某广告公司欲招聘广告策划人员一名,对A、B、C 三名候选人进行了
三项素质测试.他们的各项测试成绩如下表所示:
测试项 目 测试成绩
A B
C
创 新 72 85
67
综合知 识 50 74
70
语 言 88 45
67
Y
(1)如果根据三项测试的平均成绩确定录用人
选,那么谁将被录用
(2)根据实际需要,公司将创新、综合知识和
语言三项测试得分按4:3:1的比例确定各人的 测试成绩,此时谁将被录用
第 ( 1 ) (2)问中录用的人不一样说明了什么
探究发现
例1 某广告公司欲招聘广告策划人员一名,对A、B、C 三名候选人进行了
三项素质测试.他们的各项测试成绩如下表所示:
测试项 测试成绩
A B
C
创 新 72 85
67
综合知 识 50 74
70
语 言 88 45
67
Y
Z: 探究发现
由于测试的每一项的重要性不同,所以所占的比份也不同,计算出的平均数就不同,
因此重要性的差异对结果的影响是很大的.
实际问题中, 一组数据里的各个数据的“重要程度”未必相同,因而在计算这组数据的平
均数时,往往给每个数据一个“权”.
如例1中4,3,1分别是创新、综合知识、语言三项测试成绩的权,
为 A的三项测试成结的如权平均数
H
而
Y
跟踪训练
1、小明和小颖本学期的数学平时成绩、期中成绩、期末成绩分别如
下: (单位:分)
小明:平时85,期中90,期末92.
小颖:平时90,期中83,期末84.
假如学期总评分按平时成绩、期中成绩、期末成绩各占
2,4,6的比例来计算,那么小明和小颖的总评分谁更高 (结果
留到个 ) 85×2+90×4+92×6 ≈ 90 (分)
2+4+6 权 以比的形式出现
小颖的总评分=9 ×2 4+84×6≈85 (分)
答:小明的总评分高。
4
3
一班 二班 三班
四班
平均分数 81 90 85
80
班级人数 55 40 45
60
81×55+90×40+85×45+80×60
55+40+45+60
2. 八年级数学期末考试成绩如下:(易错题)
求八年级期末考试的数学平均分数
八年级期末考试的数学平均分数=
权以整数的形式出现
=83.4(分)
Y
3.学校进行广播操比赛,如图是20位评委给某班的评分情况统计
图,则该班的平均得分是 0)1.1 刀 。
人数/人
10 8 7
权以整数的形式出现
5
5
评分/分
10
8
9
4.某校在期末考核学生的体育成绩时,将早锻炼及体育课外活动表现
占成绩的20%,体育理论测试占30%,体育技能测试占50%.小颖的上
述成绩分别为92分、80分、84分,则小颖这学期的体育成绩是多少
解 :小颖这学期的体育成绩是
92×20%+80×30%+84×50%=84.4(分)
答:小颖这学期的体育成绩是84.4分.
权以百分比的形式出现
测试 项目 测试成绩/分 甲 乙
丙
笔试 75 80
90
面试 - 70
68
5. 综合能力题
某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试
和面试两项测试,三人的测试成绩如下表所示:
甲
P
丙
图1
*
又根据录用程序,组织200名职工利用投票推荐的方式对三人进行民主评议(没有
弃权票,每名职工只能推荐1人,三人得票率如图1所示,每得一票记作1分。
(1)请算出三人的民主评议得分。
(2)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确
到0.01)
(3)根据实际需要,单位将笔试、面试、民主评议三项测试得分按4:3:3的
比例确定个人成绩,那么谁将被录用
答案: (1)甲的民主评议得分=200×25%=50(分)
乙的民主评议得分=200×40%=80(分)
丙的民主评议得分=200×35%=70(分)
Y
77.4>77>72.9,所以候选人丙将被录用。
(2)甲的平均成绩=
乙的平均成绩= 丙的平均成绩=
因为76.67>76>72.67,所以候选人乙将被录用。
〇 厂甲的个人成绩=75×4493+350× =72. 9 (J 刀)
75+93+50
3
80+70+80
90+68+7(
Z18
三 二 - ≈72.67(分)
) 状
-3
1
( ) )
7667
0.0/
- 3
2Z(
则(1)数据4x ,4x ,4x ,4x ,4x 的平均数为
(2)4x -2,4x -2,4x -2,4x -2,4x -2 的平均数为 o
(3)4x +2,4x +2,4x +2,4x +2,4x +2 的平均数为
知识拓展
1.已知数据x ,x ,x ,X ,x 的平均数为a,
课堂小结 通过这节课的学习,你有什么样的收获
理解概念
=(×+x+…+x)
计算公式
概念
整数
比
百分比
算术平均数
权的表现形式
加权平均数
x= i"+*2" +…+" "r
H' +Wz+·+N
平均数
公式
出题小达人
以小组形式每组出一道关于算术平均数和一道
关于加权平均数的题。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
