(全)锐角三角函数知识点归纳及专项练习(无答案)
文档属性
| 名称 | (全)锐角三角函数知识点归纳及专项练习(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-11 19:56:30 | ||
图片预览



文档简介
锐角三角函数知识点归纳及专项练习
一.问题:为了绿化荒山,某地打算从位于山脚下的机井房沿山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是,为使出水口的高度为,求需要准备多长的水管?
探究:如图,与中,,,探究与的关系
结论:在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比是一个固定值.
※在中,,我们把锐角A的对边与斜边的比叫做∠A的正弦.记作
如图, 同理:
二.例题与练习:
1.例题:如图,在中, ,求和的值.
2.练习:
1.三角形在正方形网格纸中的位置如图所示,则的值是﹙ ﹚
A. B. C. D.
2.如图,在中, ,若,,则的值是( )
A. B. C. D.
3.在中,,,,则边的长是( )
A. B.3 C. D.
4.如图,已知是⊙的直径,点、在⊙上,且,.
则 = ; = .
5.在中,,于点.已知,,那么的值为( )
A. B. C. D.
三.在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的邻边与斜边的比是一个固定值,∠A的对边与邻边的比是一个固定值,
※在中,,我们把锐角A的邻边与斜边的比叫做∠A的余弦.记作
如图, 同理:
※在中,,我们把锐角A的对边与邻边的比叫做∠A的正切.记作
如图, 同理:
四.例题与练习:
例题:如图,在中,,,,求,的值.
练习:1.分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值
2.如图,在中,,,,求、的值
五.课后作业:
1.在中,,,,分别是、、的对边,则有( ?)
A.? B.? C.? D.
本题主要考查锐解三角函数的定义,同学们只要依据的图形,不难写出,从而可判断C正确.
2. 在中,,如果,那么的值为(? )
A.? B.? C.? D.
分析 本题主要考查锐解三角函数及三角变换知识。其思路是:依据条件,可求出;再由,可求出,从而,故应选D.
3.如图:是的边上一点,且点的坐标为(3,4), 则=______.
4.分别求出图中、的正弦值、余弦值和正切值
(B层)在中,,,,求的面积(用含有字母,,的式子表示)
三 角 函 数(2)
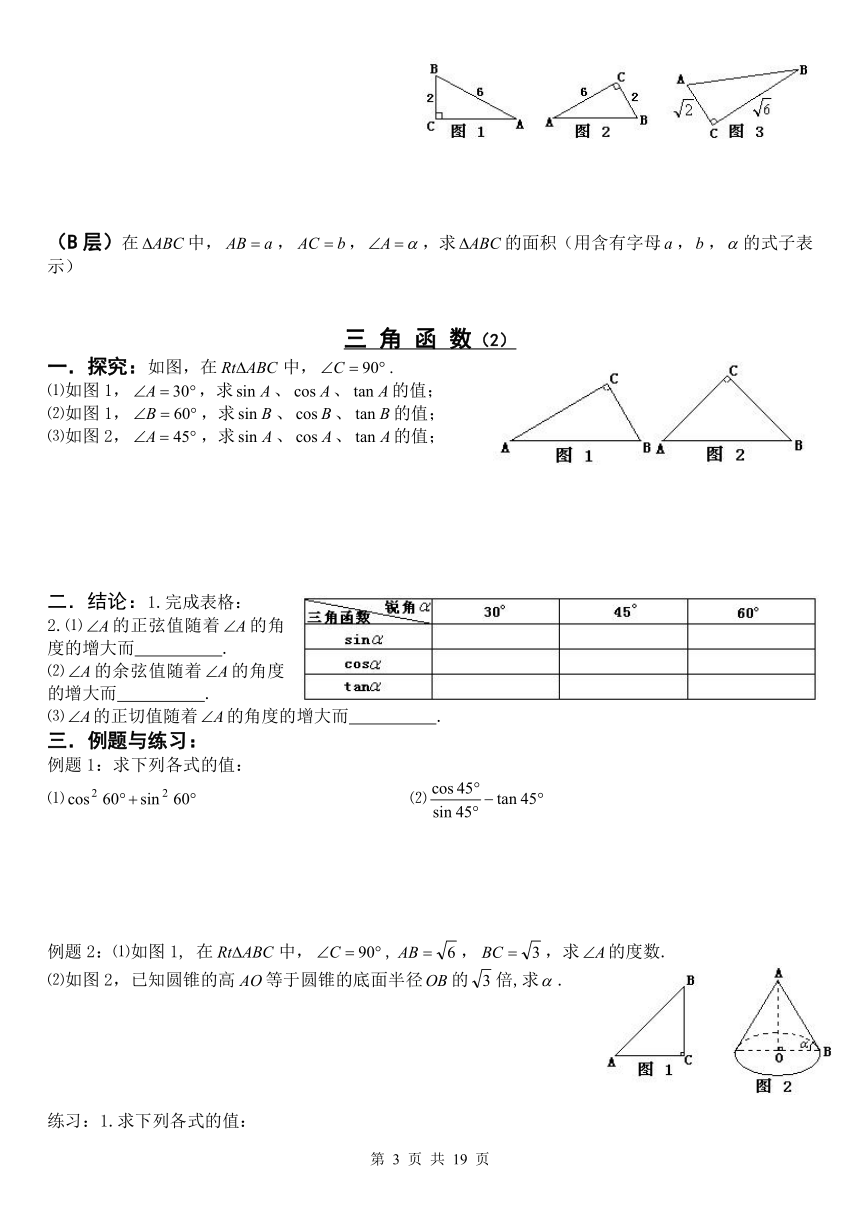
一.探究:如图,在中,.
⑴如图1,,求、、的值;
⑵如图1,,求、、的值;
⑶如图2,,求、、的值;
二.结论:1.完成表格:
2.⑴的正弦值随着的角度的增大而 .
⑵的余弦值随着的角度的增大而 .
⑶的正切值随着的角度的增大而 .
三.例题与练习:
例题1:求下列各式的值:
⑴ ⑵
例题2:⑴如图1, 在中,,,,求的度数.
⑵如图2,已知圆锥的高等于圆锥的底面半径的倍,求.
练习:1.求下列各式的值:
⑴ ⑵ ⑶
2. 在中,,,,求、的度数.
四.课堂检测:计算:
1.将改写成下列形式的式子,其中错误的是( )
A. B.
C. D.
2. 在中,,,则的值是( )
A. B. C. D.
3.在中,、都是锐角,且,,则的形状为( )
A. 直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
4.化简的结果为( )
A. B. C. D.
5.已知,则锐角的度数为 .
6.已知是锐角,若,则的值为 .
7. 在中,,,则的值为 .
8.已知,则锐角的度数为 .
9. 求下列各式的值:
⑴ ⑵
10. 在中,,,且,求、的长.
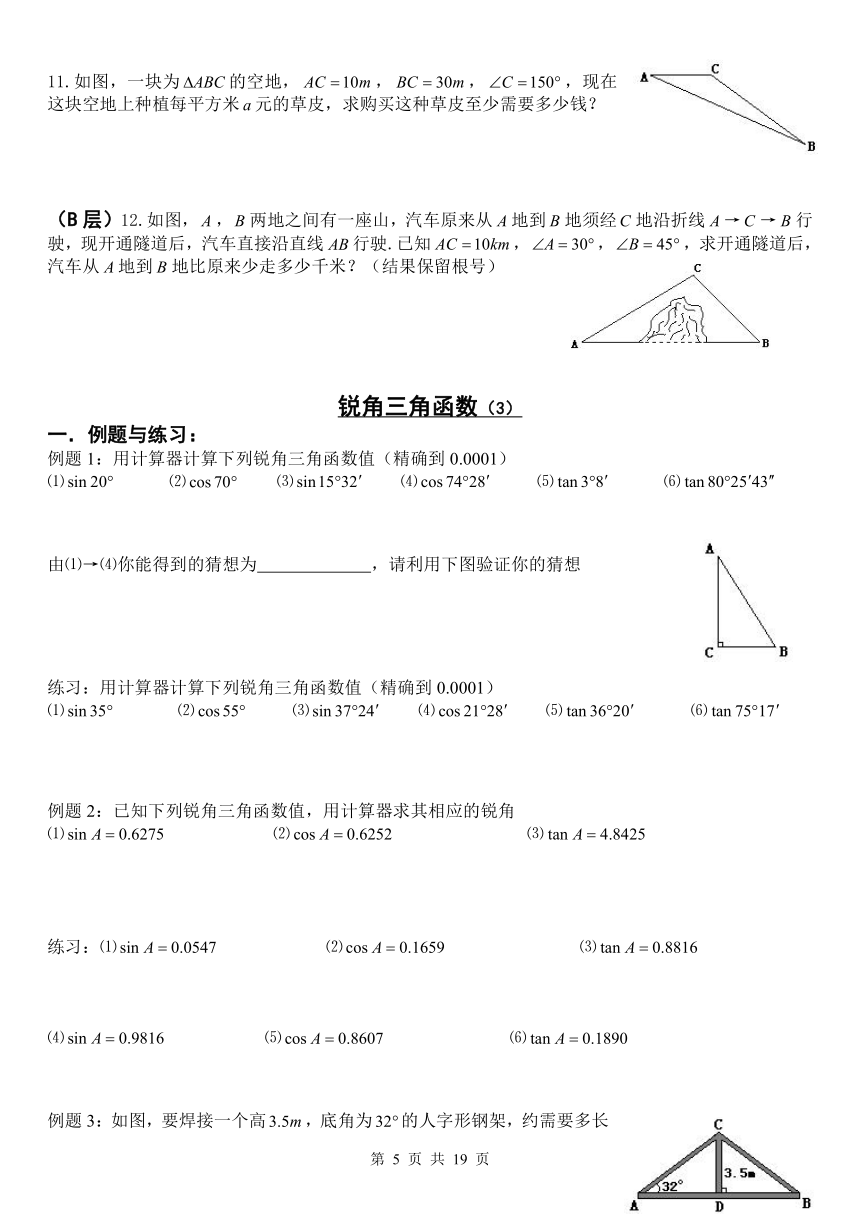
11.如图,一块为的空地,,,,现在这块空地上种植每平方米元的草皮,求购买这种草皮至少需要多少钱?
(B层)12.如图,,两地之间有一座山,汽车原来从地到地须经地沿折线→→行驶,现开通隧道后,汽车直接沿直线行驶.已知,,,求开通隧道后,汽车从地到地比原来少走多少千米?(结果保留根号)
锐角三角函数(3)
一.例题与练习:
例题1:用计算器计算下列锐角三角函数值(精确到0.0001)
⑴ ⑵ ⑶ ⑷ ⑸ ⑹
由⑴→⑷你能得到的猜想为 ,请利用下图验证你的猜想
练习:用计算器计算下列锐角三角函数值(精确到0.0001)
⑴ ⑵ ⑶ ⑷ ⑸ ⑹
例题2:已知下列锐角三角函数值,用计算器求其相应的锐角
⑴ ⑵ ⑶
练习:⑴ ⑵ ⑶
⑷ ⑸ ⑹
例题3:如图,要焊接一个高,底角为的人字形钢架,约需要多长的钢材(结果保留小数点后两位)
练习:如图,一块平行四边形木板的两条邻边、的长分别为和,它们之间的夹角为,求这块木板的面积(结果保留小数点后两位)
二.课堂检测:
1.求下列锐角三角函数值(精确到0.0001):
⑴= ; ⑵= ; = .
2. 已知下列锐角三角函数值,用计算器求其相应的锐角
⑴,= ;⑵,= ;⑶,= ;
三.课后练习:
1.计算的值为( )
A. B. C. D.
2.在中,各边的长度都扩大4倍,那么锐角的正切值( )
A.扩大4倍 B.扩大2倍 C.保持不变 D.缩小4倍
3.已知为锐角,,则等于( )
A. B. C. D.
4.如果等腰三角形的底角为,腰长为6,那么这个三角形的面积为( )
A.4.5 B. C. D.36
5.中,,,,则等于( )
A. B. C. D.
6.已知,则的度数为( )
A. B. C. D.
7.已知,则 ;若,则 ;若,则 ;
8.某人沿倾斜角为的斜坡前行了100,则他上升的最大高度为 (精确到0.01)
9.计算:⑴ ⑵
10. 已知:如图,在中,,是高,,,求、、.(精确到1)
(B层)1.要求的值,可构造如图所示的直角三角形进行计算:作,使,斜边,直角边,那么,,,在此图的基础上,通过添加适当的辅助线,可求出的值,请简要写出你添加的辅助线和求出的值.
2.如图,把矩形纸片放入平面直角坐标系中,使、分别落在轴、轴上,连接,将纸片沿折叠,使点落在点的位置,若,,求点的坐标
锐角三角函数(4)
一.问题:如图,要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角一般要满足,现有一个长的梯子,问:
⑴使用这个梯子最高可以攀上多高的墙(结果保留小数点后一位)?
⑵当梯子底端距离墙面时,这个人是否能够安全使用这个梯子?
二.解直角三角形:在中,,由 得 或由 得
三.例题与练习:
例题1:如图,在中,,,,解这个直角三角形.
练习:如上图,在中,,,,解这个直角三角形.
例题2:如图,在中,,,,解这个直角三角形(结果保留小数点后一位).
练习:如上图,在中,,,,解这个直角三角形(结果保留小数点后一位).
四.课堂检测:在中,,、、的对边分别为、和,若,,解这个直角三角形
五.课后作业:
1.在中,,、、的对边分别为、和,根据下列条件解直角三角形.
⑴, ⑵, ⑶,
2.在中,于点,且,
⑴若,求的长 ⑵若=15,求的长
3.为了测量塔高,小龙在距塔的中心点50米的处,用测角器量得仰角为,已知测角器的高度为1.52米,求塔高的长.(精确到0.1米)
4.如图所示,在离铁塔150米的处用测角仪测得塔顶仰角,已知仪器高米,求铁塔高.(精确到0.1米)
5.如图所示,从某海岛上的观察所测得海上某船只的俯角为,若观察所与海面的垂直高度米,求船只到观察所的水平距离。(精确到0.1米)
锐角三角函数(5)
一.例题与练习:
例题1:2003年10月15日“神舟”5号载人航天飞船发射成功.当飞船完成变轨后,就在离地球表面350的圆形轨道运行.如图,当飞船运行到地球表面上点的正上方时,从飞船能直接看到的地球最远的点在什么位置?这样的最远点与点的路程是多少?(地球半径约为6400,结果保留小数点后一位)
练习:如图为半径500圆形湖泊,在湖泊⊙正东方的湖岸有一抽水房,在抽水房的正西方2000处的小明想到抽水房维修机器,请你在图中画出他走的最短路线,并求出最短路程是多少?(结果保留小数点后一位)
例题2:热气球的探测器显示,从热气球看一栋高楼顶部的仰角为,看这栋高楼底部的俯角为,热气球与高楼的水平距离为120,求这栋高楼的高度(结果保留小数点后一位)
练习:某塔上有一旗杆,由距40的处观察旗杆顶部的仰角为,观察旗杆底部的仰角为,求旗杆的高度. (结果保留小数点后一位)
二.课堂检测:某校数学兴趣小组为了测量学校()的高度,利用附近的一座古塔()作为参照物,用测角仪在学校的底部处测得塔顶处的仰角,爬到楼顶的处测得塔顶处的仰角,已知学校到古塔的距离是120米,求学校的高度.(精确到0.1米)
--9--
三.课后作业:
1.如图,河旁有一座小山,从山顶处测得河对岸点的俯角为,测得岸边点的俯角为,又知河宽为50米.现需要从山顶到河对岸拉一条笔直的缆绳,求缆绳的长(答案可带根号)
2.某学校学生到旅顺白云山游玩,同时对白云塔的高度进行了测量.如图,他们在处测得塔顶的仰角为,再向塔的方向直行80步(1步=0.8)到达处,又测得塔顶的仰角为,请你用以上数据计算塔高(学生的身高忽略不计)
3.如图所示为住宅区内的两幢楼,它们的高,两幢楼间的距离,现需要了解甲楼对乙楼采光的影响情况,当太阳光线与水平线的夹角为36 时,求甲楼的影子在乙楼上有多高?(精确到0.1米)
4.如图所示,某工程队修建高速公路时,需要打通东西走向的穿山隧道,为了测得的长,工程队在山的南面选取一点,用测量仪器测得,,,请你利用所学知识求出的长.(精确到1米)
5.如图所示,直升机在跨河大桥的上方点处.此时飞机离地面的高度,且、、三点在同一直线上,测得大桥两端的俯角分别为,,求大桥的长(精确到0.1米)
锐角三角函数(6)
一.例题与练习:
例题1:如图,一艘海轮位于灯塔的北偏东方向,距离灯塔80海里的处,它沿正南方向航行一段时间后,到达位于灯塔的南偏东方向的处,这时海轮所在的处距离灯塔有多远?(结果保留小数点后一位)
练习:如图,海中有一个小岛,它的周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在点测得小岛在北偏东方向上,航行12海里到达点,这时测得小岛在北偏东方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
例题2:如图所示的梯形是水库大坝的横断面图形,斜坡的坡度,斜坡的坡度,坝顶,坝高为25.
⑴求大坝的下底宽(精确到0.1米);
⑵求斜坡的坡角的度数(精确到分).
练习:如图,拦水坝的横截面为梯形,高,斜坡的坡度,斜坡的坡度.
⑴求坡角和;
⑵求斜坡的长(结果保留小数点后一位)
二.课堂检测:如图所示的梯形是水库大坝的横断面图形,坝顶宽,斜坡,坝高8米,斜坡的坡度,求坝底宽.(精确到0.1米)
三.课后作业:
1.某城市将地处、两地的两所大学合并成一所综合性大学,为了方便两地师生来往,学校准备在相距的、两地之间修建一条笔直的公路(如图),经测量在地北偏东方向、地北偏西的处有一个半径为的公园.问计划修建的公路能否穿过公园?
2.如图,某处海面上,一艘军舰正在基地的正东方向且距地40海里的处训练,突然接到基地命令,要该舰前往岛,接送一名病重的渔民到基地医院救治.已知岛在的北偏东方向,且在的北偏西方向,军舰从处出发,平均每小时行驶20海里,需要多长时间才能把患者送到基地医院?(精确到0.1小时)
3.今年入夏以来,松花江哈尔滨段水位不断下降,达到历史最低水位。一条船在松花江某水段自西向东沿直线航行,在处测得航标在北偏东60 方向上,前进100米到达处,又测得航标在北偏东45 方向上。且知在以航标为圆心,120米长半径的圆形区内有浅滩。如果这条船继续前进,是否有被浅滩阻碍的危险?
4.如图所示的燕尾槽的横断面是等腰梯形,其中的坡度为,外口宽毫米,燕尾槽的深度是毫米,求它的里口宽(精确到1毫米)。
(B层)5.如图,在笔直的海岸线上有、、三个码头,海中有一个小岛,已知点在点的北偏东的方向,点在点的北偏东的方向,点在点的正北方向,且点到点的距离为100,现有人在码头,有急事要到小岛,现知道,船的速度为,车的速度为,为此有人设计了三种方案:
⑴方案一:由码头直接坐船到小岛
⑵方案二:由码头坐车到码头,再坐船到小岛
⑶方案三:由码头坐车到码头,再坐船到小岛
假设途中周转的时间忽略不计,请你通过计算说明哪种设计方案最好?
锐角三角函数(7)
一.测量高度的方案设计:
1.可达到被测物体底部的方案:
方案一:在有阳光的日子里,为旗杆的影子,然后竖直立起一根标杆,为标杆的影子.
探究原理:光的特征(太阳光是平行光线) 相似三角形的特征.
提供选用的测量工具有:①皮尺 ②标杆
⑴你需要得测此示意图中哪些数据?并分别用、、来表示测得数据.
⑵写出旗杆高度的计算式:= .
方案二:将标杆竖直立在地面上,人在所在直线上移动,用视线使、、三点在同一直线上.
探究原理:光沿直线传播 相似三角形的特征.
提供选用的测量工具有:①皮尺 ②标杆
⑴你需要得测此示意图中哪些数据?并分别用、、来表示测得
数据.
⑵写出旗杆高度的计算式:=
方案三:在距旗杆一定距离的地面上放一个平面镜,人在所在直线上移动,直到恰好在镜子里看见旗杆顶点为止.
探究原理:光的反射定律 相似三角形的特征.
提供选用的测量工具有:①皮尺 ②平面镜
⑴你需要得测此示意图中哪些数据?并分别用、、来表示测得数据.
⑵写出旗杆高度的计算式:= .
方案四:将测角仪竖直立在地面上.
提供选用的测量工具有:①皮尺 ②测角仪
⑴写出测量步骤.及你需要得测此示意图中的数据.并长度分别用、、,角度用、…来表示测得数据.
⑵写出旗杆高度的计算式:= .
2.不可达到被测物体底部的方案:
方案一:测量工具有:①皮尺 ②测角仪
⑴写出测量步骤.及你需要得测此示意图中的数据.并长度分别用、、,角度用、…来表示测得数据.
⑵写出山的高度的计算式:= .
方案二.如图,、是两栋地平高度相等、隔岸相望的楼房,由于建筑物密集,在的周围没有开阔地带,为了测量的高度,只能从分利用楼的空间,楼的各层都可到达并且都能看到,现仅有的测量工具为皮尺和测角器.
⑴请你设计一个测量楼高度的方案,要求写出测量步骤和必须的测量数据(用字母表示),线段长用、、…表示,角用、、…表示,并画出测量图形.
⑵用你测量的数据(用字母表示)写出计算楼高度的表达式.
二.测量宽度的方案设计:
方案一:在河的对岸选定一个目标作为点,再在河的这一边选点和,使,然后再选一点,使,用视线确定和的交点.
提供选用的测量工具有:①皮尺 ②教学用三角板
⑴你需要得测此示意图中哪些数据?并分别用、、来表示测得数据.
⑵写出河宽的计算式:=
方案二:在河的对岸选定一个目标作为点,再在河的这一边选点和,使得、、三点在一条直线上,且与河岸垂直,然后确定一点,使,用视线确定与河岸的交点.
提供选用的测量工具有:①皮尺 ②教学用三角板
⑴你需要得测此示意图中哪些数据?并分别用、、来表示测得数据.
⑵写出河宽的计算式:= .
方案三:如图,为测量小河的宽度,先在河岸边上任意取一点,再在河的另一岸取两点、,测得,,量得.
⑴求小河的宽度;
⑵请你再设计一种测量河宽度的方案,画出设计草图并作简要说明.
锐角三角函数(单元)
例题:1.如图,某校学习小组进行测量小山高度的实践活动.部分学生在山脚点测得山腰上一点的仰角为,并测得的长为180米;另一部分同学在山顶点测得山脚点的俯角为,山腰点的俯角为,请你帮助他们计算出小山的高度.(结果保留根号)
2.如图,小红面对黑板坐在凳子上,若把黑板看成一个矩形,其上的一个字看作点,过点的该矩形的高为,把小红的眼睛看作点.现测得:,视线恰好与水平线平行,视线与的夹角为,视线与的夹角为.求与的长.(精确到0.1米)
一.选择题:
1.在中,,,,则的值为( )
A. B. C. D.
2.若,则的值为( )
A.1 B. C. D.
3.如图,在把易拉罐中的水倒入一个圆水杯的过程中,若水杯中的水在点与易拉罐刚好接触,则此时水杯中的水深为( )
A.2 B.4 C.6 D.8
4.某人沿着倾斜角为的斜坡前进了米,则他上升的高度为( )
A.米 B.米 C.米 D.米
5.如图,在中,,,,则的长为( )
A. B. C. D.
6.在中,斜边是直角边的4倍,则的值为( )
A. B. C. D.
7.菱形的对角线,,则的值为( )
A. B. C. D.
8.如图的方格中,则与的正切值最接近的是( )
A. B. C. D.
二.填空题:
9.如果是等边三角形的一个内角,那么的值为 .
10.中,,,,那么的长为 .
11.在中,,,的周长为60,那么的面积为 .
12.若式子无意义,则的值为 .
13.一个等腰三角形的两边长分别为5和8,则这个等腰三角形底角的正弦值为 .
14.某人沿着山坡从山脚到山顶共走1000米,他上升的高度为500米,则这个山坡的坡度为 .
15.如图,四个边长为的小正方形,则的值为 .
16.中,若,,则的度数为_______.
17.一等腰三角形的两边长分别为4和6,则其底角的余弦值为________.
18. 中,,,若的平分线长为,则 =_____, =_______.
19.如图,在中,,,,则的长为________.
20.中,,若,,则的长为_______
三.解答题:
21.计算下面各式:
⑴ ⑵
22.在锐角中,,,求:⑴的值;⑵的值.
23.一次函数与轴、轴的交点分别为 、,若的周长为(为坐标原点),求的值.
24.某片绿地的形状如图所示,其中,,,,,求、的长(精确到1)
25.某船以每小时36海里的速度向正东方向航行,在点测得某岛在北偏东方向上,航行半小时后到达点,测得该岛在北偏东方向上,已知该岛周围16海里内有暗礁.
⑴试说明点是否在暗礁区域外?
⑵若继续向东航行有无触礁危险?请说明理由.
26.如图为某一风景区的步行台阶,为了安全着想,准备将台阶进行改善,把倾角由减至,已知原台阶的长为5米(所在地面为水平面)
⑴改善后的台阶会加长多少?(精确到0.01米)
⑵改善后的台阶会躲占多长一段地面?(精确到0.01米)
27.如图,已知某小区的两幢19层住宅楼的距离为,由地面向上依次为第1层、第2层、…、第10层,每层高度为.假设某一时刻甲楼在乙楼侧面的影长,太阳光与水平线的夹角为.
⑴用含的式子表示;
⑵当时,甲楼楼顶点的影子落在乙楼的第几层?若每小时增加,从此时起几小时后甲楼的影子刚好不影响乙楼采光?
28.如图,某人在山坡坡脚处测得某塔塔顶的仰角为,沿山坡向上走到点再测得点的仰角为,已知米,山坡的坡度为.
求塔高以及此人所在位置点的铅直高度.
29.如图,小红同学想测量河对岸一塔的高度,她先在点处测得塔顶的仰角为,这时她再往正前方前进20米到点,又测得塔顶的仰角为,求塔高
30.如图,河边有一条笔直的公路,公路两侧是平坦的草地,在一次数学活动课上,老师要求测量河对岸点到公路的距离,请你设计一个测量方案.要求:
⑴列出你测量使用的测量工具;
⑵画出测量示意图,写出测量步骤;
⑶用字母表示测得的数据,求出点到公路的距离.
31.如图,在某气象站附近海面有一台风,据监测,当台风中心位于气象站的东偏南方向100千米的海面处,并以20千米/小时的速度向西偏北方向移动,台风侵袭的范围为圆形区域,当前半径20千米,并以10千米/小时的速度不断增大,已知,问:
⑴台风中心几小时移动到气象站的正南方向处,此时气象站是否受到台风侵袭?
⑵几小时后该气象站开始受到台风侵袭?
32.如图,小岛在港口的南偏西45°方向,距离港口81海里处,甲船从出发,沿方向以9海里/时的速度驶向港口,乙船从港口出发,沿南偏东60°方向,以18海里/时的速度驶离港口.现两船同时出发.
⑴出发后几小时两船与港口的距离相等?
⑵出发后几小时乙船在甲船的正东方向?(结果精确到0.1小时)
一.问题:为了绿化荒山,某地打算从位于山脚下的机井房沿山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是,为使出水口的高度为,求需要准备多长的水管?
探究:如图,与中,,,探究与的关系
结论:在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比是一个固定值.
※在中,,我们把锐角A的对边与斜边的比叫做∠A的正弦.记作
如图, 同理:
二.例题与练习:
1.例题:如图,在中, ,求和的值.
2.练习:
1.三角形在正方形网格纸中的位置如图所示,则的值是﹙ ﹚
A. B. C. D.
2.如图,在中, ,若,,则的值是( )
A. B. C. D.
3.在中,,,,则边的长是( )
A. B.3 C. D.
4.如图,已知是⊙的直径,点、在⊙上,且,.
则 = ; = .
5.在中,,于点.已知,,那么的值为( )
A. B. C. D.
三.在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的邻边与斜边的比是一个固定值,∠A的对边与邻边的比是一个固定值,
※在中,,我们把锐角A的邻边与斜边的比叫做∠A的余弦.记作
如图, 同理:
※在中,,我们把锐角A的对边与邻边的比叫做∠A的正切.记作
如图, 同理:
四.例题与练习:
例题:如图,在中,,,,求,的值.
练习:1.分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值
2.如图,在中,,,,求、的值
五.课后作业:
1.在中,,,,分别是、、的对边,则有( ?)
A.? B.? C.? D.
本题主要考查锐解三角函数的定义,同学们只要依据的图形,不难写出,从而可判断C正确.
2. 在中,,如果,那么的值为(? )
A.? B.? C.? D.
分析 本题主要考查锐解三角函数及三角变换知识。其思路是:依据条件,可求出;再由,可求出,从而,故应选D.
3.如图:是的边上一点,且点的坐标为(3,4), 则=______.
4.分别求出图中、的正弦值、余弦值和正切值
(B层)在中,,,,求的面积(用含有字母,,的式子表示)
三 角 函 数(2)
一.探究:如图,在中,.
⑴如图1,,求、、的值;
⑵如图1,,求、、的值;
⑶如图2,,求、、的值;
二.结论:1.完成表格:
2.⑴的正弦值随着的角度的增大而 .
⑵的余弦值随着的角度的增大而 .
⑶的正切值随着的角度的增大而 .
三.例题与练习:
例题1:求下列各式的值:
⑴ ⑵
例题2:⑴如图1, 在中,,,,求的度数.
⑵如图2,已知圆锥的高等于圆锥的底面半径的倍,求.
练习:1.求下列各式的值:
⑴ ⑵ ⑶
2. 在中,,,,求、的度数.
四.课堂检测:计算:
1.将改写成下列形式的式子,其中错误的是( )
A. B.
C. D.
2. 在中,,,则的值是( )
A. B. C. D.
3.在中,、都是锐角,且,,则的形状为( )
A. 直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
4.化简的结果为( )
A. B. C. D.
5.已知,则锐角的度数为 .
6.已知是锐角,若,则的值为 .
7. 在中,,,则的值为 .
8.已知,则锐角的度数为 .
9. 求下列各式的值:
⑴ ⑵
10. 在中,,,且,求、的长.
11.如图,一块为的空地,,,,现在这块空地上种植每平方米元的草皮,求购买这种草皮至少需要多少钱?
(B层)12.如图,,两地之间有一座山,汽车原来从地到地须经地沿折线→→行驶,现开通隧道后,汽车直接沿直线行驶.已知,,,求开通隧道后,汽车从地到地比原来少走多少千米?(结果保留根号)
锐角三角函数(3)
一.例题与练习:
例题1:用计算器计算下列锐角三角函数值(精确到0.0001)
⑴ ⑵ ⑶ ⑷ ⑸ ⑹
由⑴→⑷你能得到的猜想为 ,请利用下图验证你的猜想
练习:用计算器计算下列锐角三角函数值(精确到0.0001)
⑴ ⑵ ⑶ ⑷ ⑸ ⑹
例题2:已知下列锐角三角函数值,用计算器求其相应的锐角
⑴ ⑵ ⑶
练习:⑴ ⑵ ⑶
⑷ ⑸ ⑹
例题3:如图,要焊接一个高,底角为的人字形钢架,约需要多长的钢材(结果保留小数点后两位)
练习:如图,一块平行四边形木板的两条邻边、的长分别为和,它们之间的夹角为,求这块木板的面积(结果保留小数点后两位)
二.课堂检测:
1.求下列锐角三角函数值(精确到0.0001):
⑴= ; ⑵= ; = .
2. 已知下列锐角三角函数值,用计算器求其相应的锐角
⑴,= ;⑵,= ;⑶,= ;
三.课后练习:
1.计算的值为( )
A. B. C. D.
2.在中,各边的长度都扩大4倍,那么锐角的正切值( )
A.扩大4倍 B.扩大2倍 C.保持不变 D.缩小4倍
3.已知为锐角,,则等于( )
A. B. C. D.
4.如果等腰三角形的底角为,腰长为6,那么这个三角形的面积为( )
A.4.5 B. C. D.36
5.中,,,,则等于( )
A. B. C. D.
6.已知,则的度数为( )
A. B. C. D.
7.已知,则 ;若,则 ;若,则 ;
8.某人沿倾斜角为的斜坡前行了100,则他上升的最大高度为 (精确到0.01)
9.计算:⑴ ⑵
10. 已知:如图,在中,,是高,,,求、、.(精确到1)
(B层)1.要求的值,可构造如图所示的直角三角形进行计算:作,使,斜边,直角边,那么,,,在此图的基础上,通过添加适当的辅助线,可求出的值,请简要写出你添加的辅助线和求出的值.
2.如图,把矩形纸片放入平面直角坐标系中,使、分别落在轴、轴上,连接,将纸片沿折叠,使点落在点的位置,若,,求点的坐标
锐角三角函数(4)
一.问题:如图,要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角一般要满足,现有一个长的梯子,问:
⑴使用这个梯子最高可以攀上多高的墙(结果保留小数点后一位)?
⑵当梯子底端距离墙面时,这个人是否能够安全使用这个梯子?
二.解直角三角形:在中,,由 得 或由 得
三.例题与练习:
例题1:如图,在中,,,,解这个直角三角形.
练习:如上图,在中,,,,解这个直角三角形.
例题2:如图,在中,,,,解这个直角三角形(结果保留小数点后一位).
练习:如上图,在中,,,,解这个直角三角形(结果保留小数点后一位).
四.课堂检测:在中,,、、的对边分别为、和,若,,解这个直角三角形
五.课后作业:
1.在中,,、、的对边分别为、和,根据下列条件解直角三角形.
⑴, ⑵, ⑶,
2.在中,于点,且,
⑴若,求的长 ⑵若=15,求的长
3.为了测量塔高,小龙在距塔的中心点50米的处,用测角器量得仰角为,已知测角器的高度为1.52米,求塔高的长.(精确到0.1米)
4.如图所示,在离铁塔150米的处用测角仪测得塔顶仰角,已知仪器高米,求铁塔高.(精确到0.1米)
5.如图所示,从某海岛上的观察所测得海上某船只的俯角为,若观察所与海面的垂直高度米,求船只到观察所的水平距离。(精确到0.1米)
锐角三角函数(5)
一.例题与练习:
例题1:2003年10月15日“神舟”5号载人航天飞船发射成功.当飞船完成变轨后,就在离地球表面350的圆形轨道运行.如图,当飞船运行到地球表面上点的正上方时,从飞船能直接看到的地球最远的点在什么位置?这样的最远点与点的路程是多少?(地球半径约为6400,结果保留小数点后一位)
练习:如图为半径500圆形湖泊,在湖泊⊙正东方的湖岸有一抽水房,在抽水房的正西方2000处的小明想到抽水房维修机器,请你在图中画出他走的最短路线,并求出最短路程是多少?(结果保留小数点后一位)
例题2:热气球的探测器显示,从热气球看一栋高楼顶部的仰角为,看这栋高楼底部的俯角为,热气球与高楼的水平距离为120,求这栋高楼的高度(结果保留小数点后一位)
练习:某塔上有一旗杆,由距40的处观察旗杆顶部的仰角为,观察旗杆底部的仰角为,求旗杆的高度. (结果保留小数点后一位)
二.课堂检测:某校数学兴趣小组为了测量学校()的高度,利用附近的一座古塔()作为参照物,用测角仪在学校的底部处测得塔顶处的仰角,爬到楼顶的处测得塔顶处的仰角,已知学校到古塔的距离是120米,求学校的高度.(精确到0.1米)
--9--
三.课后作业:
1.如图,河旁有一座小山,从山顶处测得河对岸点的俯角为,测得岸边点的俯角为,又知河宽为50米.现需要从山顶到河对岸拉一条笔直的缆绳,求缆绳的长(答案可带根号)
2.某学校学生到旅顺白云山游玩,同时对白云塔的高度进行了测量.如图,他们在处测得塔顶的仰角为,再向塔的方向直行80步(1步=0.8)到达处,又测得塔顶的仰角为,请你用以上数据计算塔高(学生的身高忽略不计)
3.如图所示为住宅区内的两幢楼,它们的高,两幢楼间的距离,现需要了解甲楼对乙楼采光的影响情况,当太阳光线与水平线的夹角为36 时,求甲楼的影子在乙楼上有多高?(精确到0.1米)
4.如图所示,某工程队修建高速公路时,需要打通东西走向的穿山隧道,为了测得的长,工程队在山的南面选取一点,用测量仪器测得,,,请你利用所学知识求出的长.(精确到1米)
5.如图所示,直升机在跨河大桥的上方点处.此时飞机离地面的高度,且、、三点在同一直线上,测得大桥两端的俯角分别为,,求大桥的长(精确到0.1米)
锐角三角函数(6)
一.例题与练习:
例题1:如图,一艘海轮位于灯塔的北偏东方向,距离灯塔80海里的处,它沿正南方向航行一段时间后,到达位于灯塔的南偏东方向的处,这时海轮所在的处距离灯塔有多远?(结果保留小数点后一位)
练习:如图,海中有一个小岛,它的周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在点测得小岛在北偏东方向上,航行12海里到达点,这时测得小岛在北偏东方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
例题2:如图所示的梯形是水库大坝的横断面图形,斜坡的坡度,斜坡的坡度,坝顶,坝高为25.
⑴求大坝的下底宽(精确到0.1米);
⑵求斜坡的坡角的度数(精确到分).
练习:如图,拦水坝的横截面为梯形,高,斜坡的坡度,斜坡的坡度.
⑴求坡角和;
⑵求斜坡的长(结果保留小数点后一位)
二.课堂检测:如图所示的梯形是水库大坝的横断面图形,坝顶宽,斜坡,坝高8米,斜坡的坡度,求坝底宽.(精确到0.1米)
三.课后作业:
1.某城市将地处、两地的两所大学合并成一所综合性大学,为了方便两地师生来往,学校准备在相距的、两地之间修建一条笔直的公路(如图),经测量在地北偏东方向、地北偏西的处有一个半径为的公园.问计划修建的公路能否穿过公园?
2.如图,某处海面上,一艘军舰正在基地的正东方向且距地40海里的处训练,突然接到基地命令,要该舰前往岛,接送一名病重的渔民到基地医院救治.已知岛在的北偏东方向,且在的北偏西方向,军舰从处出发,平均每小时行驶20海里,需要多长时间才能把患者送到基地医院?(精确到0.1小时)
3.今年入夏以来,松花江哈尔滨段水位不断下降,达到历史最低水位。一条船在松花江某水段自西向东沿直线航行,在处测得航标在北偏东60 方向上,前进100米到达处,又测得航标在北偏东45 方向上。且知在以航标为圆心,120米长半径的圆形区内有浅滩。如果这条船继续前进,是否有被浅滩阻碍的危险?
4.如图所示的燕尾槽的横断面是等腰梯形,其中的坡度为,外口宽毫米,燕尾槽的深度是毫米,求它的里口宽(精确到1毫米)。
(B层)5.如图,在笔直的海岸线上有、、三个码头,海中有一个小岛,已知点在点的北偏东的方向,点在点的北偏东的方向,点在点的正北方向,且点到点的距离为100,现有人在码头,有急事要到小岛,现知道,船的速度为,车的速度为,为此有人设计了三种方案:
⑴方案一:由码头直接坐船到小岛
⑵方案二:由码头坐车到码头,再坐船到小岛
⑶方案三:由码头坐车到码头,再坐船到小岛
假设途中周转的时间忽略不计,请你通过计算说明哪种设计方案最好?
锐角三角函数(7)
一.测量高度的方案设计:
1.可达到被测物体底部的方案:
方案一:在有阳光的日子里,为旗杆的影子,然后竖直立起一根标杆,为标杆的影子.
探究原理:光的特征(太阳光是平行光线) 相似三角形的特征.
提供选用的测量工具有:①皮尺 ②标杆
⑴你需要得测此示意图中哪些数据?并分别用、、来表示测得数据.
⑵写出旗杆高度的计算式:= .
方案二:将标杆竖直立在地面上,人在所在直线上移动,用视线使、、三点在同一直线上.
探究原理:光沿直线传播 相似三角形的特征.
提供选用的测量工具有:①皮尺 ②标杆
⑴你需要得测此示意图中哪些数据?并分别用、、来表示测得
数据.
⑵写出旗杆高度的计算式:=
方案三:在距旗杆一定距离的地面上放一个平面镜,人在所在直线上移动,直到恰好在镜子里看见旗杆顶点为止.
探究原理:光的反射定律 相似三角形的特征.
提供选用的测量工具有:①皮尺 ②平面镜
⑴你需要得测此示意图中哪些数据?并分别用、、来表示测得数据.
⑵写出旗杆高度的计算式:= .
方案四:将测角仪竖直立在地面上.
提供选用的测量工具有:①皮尺 ②测角仪
⑴写出测量步骤.及你需要得测此示意图中的数据.并长度分别用、、,角度用、…来表示测得数据.
⑵写出旗杆高度的计算式:= .
2.不可达到被测物体底部的方案:
方案一:测量工具有:①皮尺 ②测角仪
⑴写出测量步骤.及你需要得测此示意图中的数据.并长度分别用、、,角度用、…来表示测得数据.
⑵写出山的高度的计算式:= .
方案二.如图,、是两栋地平高度相等、隔岸相望的楼房,由于建筑物密集,在的周围没有开阔地带,为了测量的高度,只能从分利用楼的空间,楼的各层都可到达并且都能看到,现仅有的测量工具为皮尺和测角器.
⑴请你设计一个测量楼高度的方案,要求写出测量步骤和必须的测量数据(用字母表示),线段长用、、…表示,角用、、…表示,并画出测量图形.
⑵用你测量的数据(用字母表示)写出计算楼高度的表达式.
二.测量宽度的方案设计:
方案一:在河的对岸选定一个目标作为点,再在河的这一边选点和,使,然后再选一点,使,用视线确定和的交点.
提供选用的测量工具有:①皮尺 ②教学用三角板
⑴你需要得测此示意图中哪些数据?并分别用、、来表示测得数据.
⑵写出河宽的计算式:=
方案二:在河的对岸选定一个目标作为点,再在河的这一边选点和,使得、、三点在一条直线上,且与河岸垂直,然后确定一点,使,用视线确定与河岸的交点.
提供选用的测量工具有:①皮尺 ②教学用三角板
⑴你需要得测此示意图中哪些数据?并分别用、、来表示测得数据.
⑵写出河宽的计算式:= .
方案三:如图,为测量小河的宽度,先在河岸边上任意取一点,再在河的另一岸取两点、,测得,,量得.
⑴求小河的宽度;
⑵请你再设计一种测量河宽度的方案,画出设计草图并作简要说明.
锐角三角函数(单元)
例题:1.如图,某校学习小组进行测量小山高度的实践活动.部分学生在山脚点测得山腰上一点的仰角为,并测得的长为180米;另一部分同学在山顶点测得山脚点的俯角为,山腰点的俯角为,请你帮助他们计算出小山的高度.(结果保留根号)
2.如图,小红面对黑板坐在凳子上,若把黑板看成一个矩形,其上的一个字看作点,过点的该矩形的高为,把小红的眼睛看作点.现测得:,视线恰好与水平线平行,视线与的夹角为,视线与的夹角为.求与的长.(精确到0.1米)
一.选择题:
1.在中,,,,则的值为( )
A. B. C. D.
2.若,则的值为( )
A.1 B. C. D.
3.如图,在把易拉罐中的水倒入一个圆水杯的过程中,若水杯中的水在点与易拉罐刚好接触,则此时水杯中的水深为( )
A.2 B.4 C.6 D.8
4.某人沿着倾斜角为的斜坡前进了米,则他上升的高度为( )
A.米 B.米 C.米 D.米
5.如图,在中,,,,则的长为( )
A. B. C. D.
6.在中,斜边是直角边的4倍,则的值为( )
A. B. C. D.
7.菱形的对角线,,则的值为( )
A. B. C. D.
8.如图的方格中,则与的正切值最接近的是( )
A. B. C. D.
二.填空题:
9.如果是等边三角形的一个内角,那么的值为 .
10.中,,,,那么的长为 .
11.在中,,,的周长为60,那么的面积为 .
12.若式子无意义,则的值为 .
13.一个等腰三角形的两边长分别为5和8,则这个等腰三角形底角的正弦值为 .
14.某人沿着山坡从山脚到山顶共走1000米,他上升的高度为500米,则这个山坡的坡度为 .
15.如图,四个边长为的小正方形,则的值为 .
16.中,若,,则的度数为_______.
17.一等腰三角形的两边长分别为4和6,则其底角的余弦值为________.
18. 中,,,若的平分线长为,则 =_____, =_______.
19.如图,在中,,,,则的长为________.
20.中,,若,,则的长为_______
三.解答题:
21.计算下面各式:
⑴ ⑵
22.在锐角中,,,求:⑴的值;⑵的值.
23.一次函数与轴、轴的交点分别为 、,若的周长为(为坐标原点),求的值.
24.某片绿地的形状如图所示,其中,,,,,求、的长(精确到1)
25.某船以每小时36海里的速度向正东方向航行,在点测得某岛在北偏东方向上,航行半小时后到达点,测得该岛在北偏东方向上,已知该岛周围16海里内有暗礁.
⑴试说明点是否在暗礁区域外?
⑵若继续向东航行有无触礁危险?请说明理由.
26.如图为某一风景区的步行台阶,为了安全着想,准备将台阶进行改善,把倾角由减至,已知原台阶的长为5米(所在地面为水平面)
⑴改善后的台阶会加长多少?(精确到0.01米)
⑵改善后的台阶会躲占多长一段地面?(精确到0.01米)
27.如图,已知某小区的两幢19层住宅楼的距离为,由地面向上依次为第1层、第2层、…、第10层,每层高度为.假设某一时刻甲楼在乙楼侧面的影长,太阳光与水平线的夹角为.
⑴用含的式子表示;
⑵当时,甲楼楼顶点的影子落在乙楼的第几层?若每小时增加,从此时起几小时后甲楼的影子刚好不影响乙楼采光?
28.如图,某人在山坡坡脚处测得某塔塔顶的仰角为,沿山坡向上走到点再测得点的仰角为,已知米,山坡的坡度为.
求塔高以及此人所在位置点的铅直高度.
29.如图,小红同学想测量河对岸一塔的高度,她先在点处测得塔顶的仰角为,这时她再往正前方前进20米到点,又测得塔顶的仰角为,求塔高
30.如图,河边有一条笔直的公路,公路两侧是平坦的草地,在一次数学活动课上,老师要求测量河对岸点到公路的距离,请你设计一个测量方案.要求:
⑴列出你测量使用的测量工具;
⑵画出测量示意图,写出测量步骤;
⑶用字母表示测得的数据,求出点到公路的距离.
31.如图,在某气象站附近海面有一台风,据监测,当台风中心位于气象站的东偏南方向100千米的海面处,并以20千米/小时的速度向西偏北方向移动,台风侵袭的范围为圆形区域,当前半径20千米,并以10千米/小时的速度不断增大,已知,问:
⑴台风中心几小时移动到气象站的正南方向处,此时气象站是否受到台风侵袭?
⑵几小时后该气象站开始受到台风侵袭?
32.如图,小岛在港口的南偏西45°方向,距离港口81海里处,甲船从出发,沿方向以9海里/时的速度驶向港口,乙船从港口出发,沿南偏东60°方向,以18海里/时的速度驶离港口.现两船同时出发.
⑴出发后几小时两船与港口的距离相等?
⑵出发后几小时乙船在甲船的正东方向?(结果精确到0.1小时)
