北师大版数学七年级上 册第三章 整式及其加减 3.5 探索与表达规律课件(共18张PPT)
文档属性
| 名称 | 北师大版数学七年级上 册第三章 整式及其加减 3.5 探索与表达规律课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 10:27:49 | ||
图片预览






文档简介
(共18张PPT)
第三章 整式及其加减
3.5 探索与表达规律
1.经历探索数量关系,运用符号表示规律的过程;
一、学习目标
2.会用代数式表示简单问题中的数量关系.
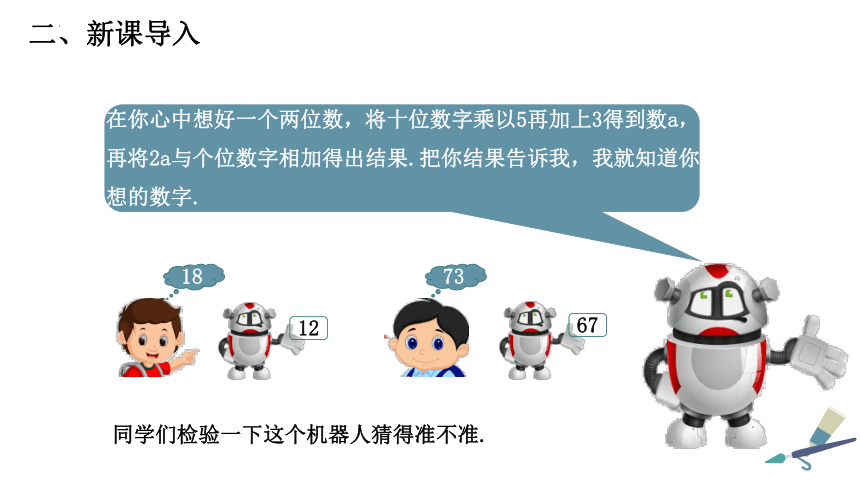
二、新课导入
在你心中想好一个两位数,将十位数字乘以5再加上3得到数a,再将2a与个位数字相加得出结果.把你结果告诉我,我就知道你想的数字.
18
73
12
67
同学们检验一下这个机器人猜得准不准.
二、新课导入
你们知道我是怎么猜出来的吗?
假设一个数十位数字是x,个位数字是y,那这个数的值为10x+y;现在将x乘5加3得到a,a=5x+3,最后计算2a+y=2(5x+3)+y=10x+y+6,所以这个结果就是想好的两位数加上6.
这个数字游戏是不是很有趣?接下来我们来发现更多有趣的东西.
三、概念剖析
探索、表达规律
观察下面的日历,并根据提示找规律.
方框中的9个数和是多少?与正中间的数9
有什么关系?
再换这组数试试结果又如何?
和是81,81是9的9倍.
和是171,171是19的9倍.
三、概念剖析
探索、表达规律
为了能够更好地表示这个规律,我们不妨设中间的数为a,其他8
个数如下表所示:
a
a-1
a+1
a-6
a-7
a-8
a+6
a+8
a+7
这9个数的和为(a-8)+(a-7)+(a-6)+(a-1)+a
+(a+1)+(a+6)+(a+7)+(a+8)=9a
显然,这个规律对于任何一个月的日历都成立.
想一想:如果将方框换成其他形状,又有哪些规律呢?
规律:方框内9数之和=9×中间数.
三、概念剖析
探索、表达规律
a
a-1
a+1
a-7
a+7
十字形框中的5个数和与正中间的数有什么关系?
同样我们设中间的数为a,
其他数如右所示:
这5个数的和为:(a-1)+(a-1)+a+(a-1)+(a-1)=5a
故得出规律:十字形框内5数之和=5×中间数.
三、概念剖析
a-1
a+1
a-8
a+6
a
a-6
a+8
H形框内7数之和与正中间的数关系又是怎样?
设正中间的数为a,其他的数如下图所示:
这7个数之和为:(a-8)+(a-6)+(a-1)+a+(a+1)+(a+6)++(a+8)=7a
故得出规律:H形框内7数之和=7×中间数.
探索、表达规律
三、概念剖析
思考:还能设计其他形状的框满足这个规律吗?
总结:探索规律的一般步骤,先寻找数量关系,用代数式表示规律,
最后验证规律.
探索、表达规律
四、典型例题
例1.如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,“?”的值为多少?
1
2
3
4
4
6
28
15
3
6
8
?
解:通过观察发现3=1×(2+1),15=3×(4+1),28=4×(6+1);
∴ =6×(8+1)=54.
四、典型例题
例2.甲、乙、丙三位同学围成一圈玩循环报数游戏,规定:①甲、乙、丙首次报出的数依次1,2,3,接着甲报4、乙报5...,按此规律,后一位同学报出的数比前一位同学报出的数大1,当报到的数是2019时,报数结束;②若报出的数为偶数,则报该数的同学需要拍手一次,在此过程中,丙同学拍手的次数是多少?
分析:设丙同学第n次报的数为an(n为正整数),根据
报数的规律可找出an=3n且丙同学报的数奇偶交替出现,
再结合2019=3×673,673÷2=336.5,即可找出结论.
四、典型例题
解:设丙同学第n次报的数为an(n为正整数),
根据题意得:a1=3,a2=6,a3=9,a4=12,a5=15,…,
∴an=3n.
∴丙同学报的数奇偶交替出现.
∵2019=3×673,673÷2=336.5,
∴丙同学需要拍手的次数为336.
【当堂检测】
1.观察下列式子:2×4+1=9=32,4×6+1=25=52,6×8+1=49=72…,根据此规律,第n个等式可以表示为 .
2n×2(n+1)+1=(2n+1)2
【当堂检测】
2.下列每个“田”字中的数据都按相同的规律排列,其最后一个“田”字中a的值为多少?
......
3
1
5
2
4
2
10
3
b
a
82
c
5
3
17
4
分析:从前三个方框中可知a、b、c是三个连续的整数,且第四个数和
第三个数c的关系是:c2+1=第四个数.
解:由c2+1=82,可得c=9,又因为a比c小1,所以a=8.
四、典型例题
例3.某我们将如图所示的排列形式的点的个数叫做“平行四边形数”.
设第n个“平行四边形数”为a,当n=60时,a的值是多少?
...
分析:由图中规律可知a=2n+2,将n=60代入a=2n+2可得a的值.
解:由图可知:a=2n+2,当n=60,a=2×60+2=122;
即当n=60时,a的值是122.
四、典型例题
例4.某同学用棋子摆成以下图案.
…
( 1 )
( 2 )
( 3 )
图案编号 (1) (2) (3) (4) (5) …
棋子个数 …
(1)填表.
(2)摆第n个图形需要 个棋子.
(6n-1)
5
11
17
23
29
【当堂检测】
3.下列图案由边长相等的蓝、白两色正方形按一定规律拼接而成.依此规律,第5个图案中白色正方形有 个.
第1个
第2个
第3个
28
【当堂检测】
4.如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这个规律摆下去,则第n个图形需要黑色的棋子的个数是 .
n(n+2)
第三章 整式及其加减
3.5 探索与表达规律
1.经历探索数量关系,运用符号表示规律的过程;
一、学习目标
2.会用代数式表示简单问题中的数量关系.
二、新课导入
在你心中想好一个两位数,将十位数字乘以5再加上3得到数a,再将2a与个位数字相加得出结果.把你结果告诉我,我就知道你想的数字.
18
73
12
67
同学们检验一下这个机器人猜得准不准.
二、新课导入
你们知道我是怎么猜出来的吗?
假设一个数十位数字是x,个位数字是y,那这个数的值为10x+y;现在将x乘5加3得到a,a=5x+3,最后计算2a+y=2(5x+3)+y=10x+y+6,所以这个结果就是想好的两位数加上6.
这个数字游戏是不是很有趣?接下来我们来发现更多有趣的东西.
三、概念剖析
探索、表达规律
观察下面的日历,并根据提示找规律.
方框中的9个数和是多少?与正中间的数9
有什么关系?
再换这组数试试结果又如何?
和是81,81是9的9倍.
和是171,171是19的9倍.
三、概念剖析
探索、表达规律
为了能够更好地表示这个规律,我们不妨设中间的数为a,其他8
个数如下表所示:
a
a-1
a+1
a-6
a-7
a-8
a+6
a+8
a+7
这9个数的和为(a-8)+(a-7)+(a-6)+(a-1)+a
+(a+1)+(a+6)+(a+7)+(a+8)=9a
显然,这个规律对于任何一个月的日历都成立.
想一想:如果将方框换成其他形状,又有哪些规律呢?
规律:方框内9数之和=9×中间数.
三、概念剖析
探索、表达规律
a
a-1
a+1
a-7
a+7
十字形框中的5个数和与正中间的数有什么关系?
同样我们设中间的数为a,
其他数如右所示:
这5个数的和为:(a-1)+(a-1)+a+(a-1)+(a-1)=5a
故得出规律:十字形框内5数之和=5×中间数.
三、概念剖析
a-1
a+1
a-8
a+6
a
a-6
a+8
H形框内7数之和与正中间的数关系又是怎样?
设正中间的数为a,其他的数如下图所示:
这7个数之和为:(a-8)+(a-6)+(a-1)+a+(a+1)+(a+6)++(a+8)=7a
故得出规律:H形框内7数之和=7×中间数.
探索、表达规律
三、概念剖析
思考:还能设计其他形状的框满足这个规律吗?
总结:探索规律的一般步骤,先寻找数量关系,用代数式表示规律,
最后验证规律.
探索、表达规律
四、典型例题
例1.如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,“?”的值为多少?
1
2
3
4
4
6
28
15
3
6
8
?
解:通过观察发现3=1×(2+1),15=3×(4+1),28=4×(6+1);
∴ =6×(8+1)=54.
四、典型例题
例2.甲、乙、丙三位同学围成一圈玩循环报数游戏,规定:①甲、乙、丙首次报出的数依次1,2,3,接着甲报4、乙报5...,按此规律,后一位同学报出的数比前一位同学报出的数大1,当报到的数是2019时,报数结束;②若报出的数为偶数,则报该数的同学需要拍手一次,在此过程中,丙同学拍手的次数是多少?
分析:设丙同学第n次报的数为an(n为正整数),根据
报数的规律可找出an=3n且丙同学报的数奇偶交替出现,
再结合2019=3×673,673÷2=336.5,即可找出结论.
四、典型例题
解:设丙同学第n次报的数为an(n为正整数),
根据题意得:a1=3,a2=6,a3=9,a4=12,a5=15,…,
∴an=3n.
∴丙同学报的数奇偶交替出现.
∵2019=3×673,673÷2=336.5,
∴丙同学需要拍手的次数为336.
【当堂检测】
1.观察下列式子:2×4+1=9=32,4×6+1=25=52,6×8+1=49=72…,根据此规律,第n个等式可以表示为 .
2n×2(n+1)+1=(2n+1)2
【当堂检测】
2.下列每个“田”字中的数据都按相同的规律排列,其最后一个“田”字中a的值为多少?
......
3
1
5
2
4
2
10
3
b
a
82
c
5
3
17
4
分析:从前三个方框中可知a、b、c是三个连续的整数,且第四个数和
第三个数c的关系是:c2+1=第四个数.
解:由c2+1=82,可得c=9,又因为a比c小1,所以a=8.
四、典型例题
例3.某我们将如图所示的排列形式的点的个数叫做“平行四边形数”.
设第n个“平行四边形数”为a,当n=60时,a的值是多少?
...
分析:由图中规律可知a=2n+2,将n=60代入a=2n+2可得a的值.
解:由图可知:a=2n+2,当n=60,a=2×60+2=122;
即当n=60时,a的值是122.
四、典型例题
例4.某同学用棋子摆成以下图案.
…
( 1 )
( 2 )
( 3 )
图案编号 (1) (2) (3) (4) (5) …
棋子个数 …
(1)填表.
(2)摆第n个图形需要 个棋子.
(6n-1)
5
11
17
23
29
【当堂检测】
3.下列图案由边长相等的蓝、白两色正方形按一定规律拼接而成.依此规律,第5个图案中白色正方形有 个.
第1个
第2个
第3个
28
【当堂检测】
4.如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这个规律摆下去,则第n个图形需要黑色的棋子的个数是 .
n(n+2)
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
