人教版九年级数学上册 22.1.3二次函数y=a(x-h)2+k的图象和性质(1)课件 (共36张PPT)
文档属性
| 名称 | 人教版九年级数学上册 22.1.3二次函数y=a(x-h)2+k的图象和性质(1)课件 (共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 507.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 10:30:04 | ||
图片预览











文档简介
(共36张PPT)
第二十二章 二次函数
22.1.3 二次函数y=a(x-h)2+k的图象和性质(1)
九年级数学上 新课标 [人]
目前国内最大跨度的钢筋混凝土拱桥——永和桥是南宁市一标志性建筑,其拱形为抛物线的一部分(如右图所示),在正常情况下,位于水面上的桥拱跨度AB长为350 m,拱高为85 m.图中的抛物线与抛物线y=ax2(a<0)有什么位置关系呢
二次函数y=ax2+k的图象和性质
在同一平面直角坐标系中,画出二次函数y=2x2,y=2x2+1,y=2x2-1的图象.
x … -1.5 -1 -0.5 0 0.5 1 1.5 …
y=2x2 … 4.5 2 0.5 0 0.5 2 4.5 …
y=2x2+1 … 5.5 3 1.5 1 1.5 3 5.5 …
y=2x2-1 … 3.5 1 -0.5 -1 -0.5 1 3.5 …
(1)自变量x的取值范围是什么
(2)画函数图象时,x取哪些值列表能使函数图象上的点均匀对称
(3)如何用平滑的曲线连接各点
y=x2-1
y=2x2
y=x2+1
(1)求出三条抛物线的开口方向、对称轴、顶点坐标.
(2)你有什么方法把抛物线y=2x2分别移动到抛物线y=2x2+1的位置和抛物线y=2x2-1的位置
抛物线 开口方向 对称轴 顶点坐标
y=2x2 向上 x=0(或y轴) (0,0)
y=2x2+1 向上 x=0(或y轴) (0,1)
y=2x2-1 向上 x=0(或y轴) (0,-1)
把抛物线y=2x2向上平移1个单位长度,就得到抛物线y=2x2+1.
把抛物线y=2x2向下平移1个单位长度,就得到抛物线y=2x2-1.
结论
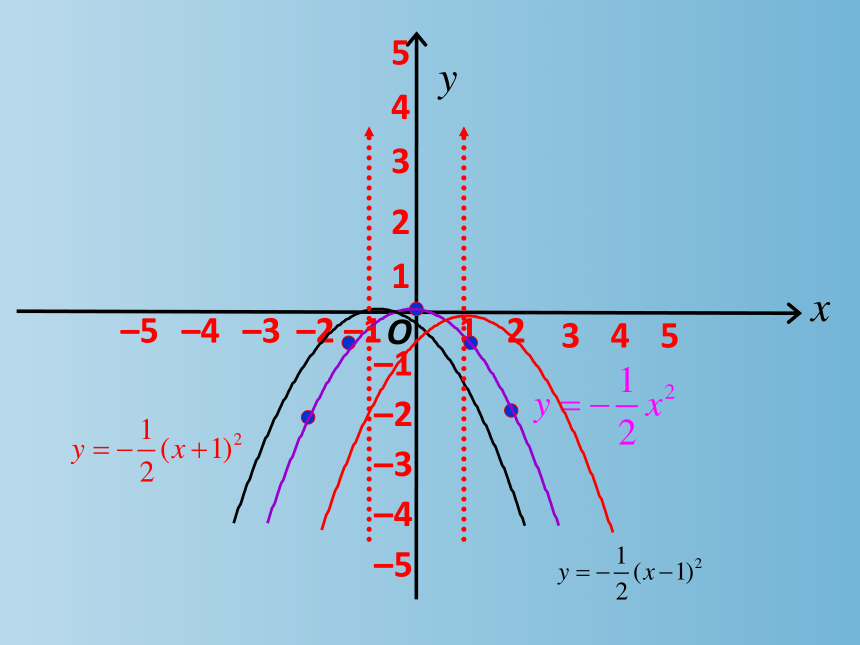
二次函数y=a(x-h)2的图象和性质
(1)在同一平面直角坐标系中,画出二次函数
的图象。
O
x
1
2
3
4
5
1
2
3
4
5
–5
–4
–3
–2
–1
–5
–4
–3
–2
–1
y
将下表补充完整
抛物线 开口方向 对称轴 顶点坐标
y=- x2
y=- (x-1)2
y=- (x+1)2
x=0
向下
向下
向下
x=-1
x=1
(0,0)
(-1,0)
(1,0)
平移时,一般按照“左加右减”的规律进行.例如,把二次函数y=ax2的图象沿x轴向左平移2个单位长度后,可以得到二次函数y=a(x+2)2的图象.把二次函数y=ax2的图象沿x轴向右平移2个单位长度后,可以得到二次函数y=a(x-2)2的图象.
一般地,抛物线y=a(x-h)2有如下性质:
①当a>0时,开口向上,当a<0时,开口向下.
②对称轴是直线x=h.
③顶点坐标是(h,0).
④ |a|越大,开口越小.
⑤二次函数y=a(x-h)2的图象可由二次函数y=ax2的图象经过左、右平移得到.当h>0时,二次函数y=a(x-h)2的图象可看成是由二次函数y=ax2的图象向右平移h个单位长度得到的.当h<0时,二次函数y=a(x-h)2的图象可看成是由二次函数y=ax2的图象向左平移|h|个单位长度得到的.
对于二次函数y=a(x-h)2(a≠0)图象上的两点A(x1,y1),B(x2,y2),当a>0时,若|x1-h|<|x2-h|,则y1< y2;当a<0时,若|x1-h|<|x2-h|,则y1>y2;对于任何a≠0时,若|x1-h|=|x2-h|,则y1= y2
二次函数y=ax2+k与y=a(x-h)2的性质.
表达式 a的 符号 开口 方向 对称轴 顶点坐标 增减性 最值
y=ax2+k
y= a(x-h)2
a>0
a<0
a>0
a<0
向上
向下
向上
向下
y轴
y轴
直线
x=h
直线
x=h
(0,k)
(0,k)
(h,0)
(h,0)
当x>0时,y随x的增大而增大
当x<0时, y随x的增大而减小
当x>0时, y随x的增大而减小
当x<0时, y随x的增大而增大
当x>h时, y随x的增大而增大
当x当x>h时, y随x的增大而减小
当x当x=0时,
y最小值=k
当x=0时,
y最大值=k
当x=h时,
y最小值=0
当x=h时,
y最大值=0
1.下列抛物线的顶点坐标为(0,1)的是( )
A.y=x2+1 B.y=x2-1
C.y=(x+1)2 D.y=(x-1)2
A
2.抛物线y=-x2-1的开口方向和对称轴分
别是 ( )
A.向上,y轴 B.向下,y轴
C.向上,直线x=-1 D.向下,直线x=-1
B
3.在平面直角坐标系中,将二次函数y=2x2的图象向上平移2个单位长度,所得图象对应的函数解析式为 ( )
A.y=2x2+2 B.y=2x2-2
C.y=2(x+2)2 D.y=2(x-2)2
A
4.抛物线y=-3(x-2)2的开口向 ,对称轴是 .
下
直线x=2
5.抛物线y=-3x2向左平移3个单位长度,所得图象对应的函数解析式为 ,平移前后的图象形状 ,当x= 时,y有
最 值,为 .
y=-3(x+3)2
相同
-3
大
0
第二十二章 二次函数
22.1.3 二次函数y=a(x-h)2+k的图象和性质(2)
九年级数学上 新课标 [人]
讨论表格中前三个函数的内容
y=- x2 y=- x2-1 y =- (x+1)2 y=- (x+1)2-1
开口 方向
对称 轴
顶点 坐标
最值
增减 性
二次函数 的图象经过怎样的平移可以得到二次函数 和 的图象
在同一直角坐标系中,画出二次函数 和
的图象.
(1)二次函数
的图象与二次函数
的图象的相同点是 、 ;不同点是 、 .
(2)①抛物线
经过怎样的平移可以得到抛物线
?
②抛物线
经过怎样的平移可以得到抛物线
?
③抛物线
经过怎样的平移可以得到抛物线
?
总结结论:把抛物线
向左平移1个单位长度,再向下平移1个单位长度,就得到抛物线 .
(3)观察抛物线y=x2,y=(x-1)2,y=(x-1)2+1,你能用类比的方法判断这三条抛物线之间的位置关系吗
结论:这三条抛物线的开口方向和开口大小相同,顶点坐标不同,只有抛物线y=(x-1)2和抛物线y=(x-1)2+1的对称轴相同;抛物线y=x2向右平移1个单位长度,再向上平移1个单位长度,就得到抛物线y=(x-1)2+1.
(4)如果a>0,当xh时,y随x的增大而增大.如果a<0,当xh时,y随x的增大而减小.
抛物线y=a(x-h)2+k有如下特点:
(1)当a>0时,开口向上;当a<0时,开口向下.
(2)对称轴是直线x=h.
(3)顶点坐标是(h,k).
(5)将抛物线y=ax2先向上或向下平移|k|个单位长度(k>0时,向上平移;k<0时,向下平移),可得到抛物线y=ax2+k,然后再将抛物线y=ax2+k向左或向右平移|h|个单位长度(h>0时,向右平移;h<0时,向左平移),就可以得到抛物线y=a(x-h)2+k,当然也可以先左、右移,再上、下移.
要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1 m处达到最高,高度为3 m,水柱落地处离池中心3 m,水管应多长
解:如图所示,以水管与地面交点为原点,原点与水柱落地处所在直线为x轴,水管所在直线为y轴,建立直角坐标系.
点(1,3)是图中这段抛物线的顶点,因此可设这段抛物线对应的函数解析式是: y=a(x-1)2+3(0≤x≤3).
由这段抛物线经过点(3,0),可得0= a(3-1)2+3,解得 因此y=- (x-1)2+3(0≤x≤3).
当x= 0时,y=2.25.也就是说,水管应2.25 m长.
x
y
二次函数 表达式 a的符号 开口方向 对称轴 顶点坐标 增减性 最值
y=ax2+k a>0 向上 y轴 (0,k) 当x>0时,y随x的增大而增大 当x<0时,y随x的增大而减小 当x=0时,
y有最小值,
y最小值=k
a<0 向下 y轴 (0,k) 当x>0时,y随x的增大而减小 当x<0时,y随x的增大而增大 当x=0时,
y有最大值,
y最大值=k
y=a(x-h)2 a>0 向上 直线 x=h (h,0) 当x>h时,y随x的增大而增大 当xy有最小值,
y最小值=0
a<0 向下 直线 x=h (h,0) 当x>h时,y随x的增大而减小 当xy有最大值,
y最大值=0
y=a(x-h)2+k a>0 向上 直线 x=h (h,k) 当x>h时,y随x的增大而增大 当xy有最小值,
y最小值=k
a<0 向下 直线 x=h (h,k) 当x>h时,y随x的增大而减小 当xy有最大值,
y最大值=k
1.对于二次函数y=(x-1)2+2的图象,下列说法正确的是 ( )
A.开口向下 B.对称轴是直线x=-1
C.顶点坐标是(1,2) D.与x轴有两个交点
C
2.将二次函数y=x2的图象向右平移1个单位长度,再向上平移2个单位长度后,所得图象对应的函数解析式为 ( )
A.y=(x-1)2+2 B.y=(x+1)2+2
C.y=(x-1)2-2 D.y=(x+1)2-2
A
3.如图所示,在平面直角坐标系中,抛物线所表示的函数解析式为y=-2(x-h)2+k,则下列结论正确的是 ( )
A.h>0,k>0
B.h<0,k>0
C.h<0,k<0
D.h>0,k<0
A
4.二次函数y=(x-1)2+3的最小值为 .
3
5.抛物线 是由抛物线
先向 (填“左”或“右”)平移
个单位长度,再向 (填“上”或“下”)平移 个单位长度得到的.
左
3
下
2
谢 谢 观 看
第二十二章 二次函数
22.1.3 二次函数y=a(x-h)2+k的图象和性质(1)
九年级数学上 新课标 [人]
目前国内最大跨度的钢筋混凝土拱桥——永和桥是南宁市一标志性建筑,其拱形为抛物线的一部分(如右图所示),在正常情况下,位于水面上的桥拱跨度AB长为350 m,拱高为85 m.图中的抛物线与抛物线y=ax2(a<0)有什么位置关系呢
二次函数y=ax2+k的图象和性质
在同一平面直角坐标系中,画出二次函数y=2x2,y=2x2+1,y=2x2-1的图象.
x … -1.5 -1 -0.5 0 0.5 1 1.5 …
y=2x2 … 4.5 2 0.5 0 0.5 2 4.5 …
y=2x2+1 … 5.5 3 1.5 1 1.5 3 5.5 …
y=2x2-1 … 3.5 1 -0.5 -1 -0.5 1 3.5 …
(1)自变量x的取值范围是什么
(2)画函数图象时,x取哪些值列表能使函数图象上的点均匀对称
(3)如何用平滑的曲线连接各点
y=x2-1
y=2x2
y=x2+1
(1)求出三条抛物线的开口方向、对称轴、顶点坐标.
(2)你有什么方法把抛物线y=2x2分别移动到抛物线y=2x2+1的位置和抛物线y=2x2-1的位置
抛物线 开口方向 对称轴 顶点坐标
y=2x2 向上 x=0(或y轴) (0,0)
y=2x2+1 向上 x=0(或y轴) (0,1)
y=2x2-1 向上 x=0(或y轴) (0,-1)
把抛物线y=2x2向上平移1个单位长度,就得到抛物线y=2x2+1.
把抛物线y=2x2向下平移1个单位长度,就得到抛物线y=2x2-1.
结论
二次函数y=a(x-h)2的图象和性质
(1)在同一平面直角坐标系中,画出二次函数
的图象。
O
x
1
2
3
4
5
1
2
3
4
5
–5
–4
–3
–2
–1
–5
–4
–3
–2
–1
y
将下表补充完整
抛物线 开口方向 对称轴 顶点坐标
y=- x2
y=- (x-1)2
y=- (x+1)2
x=0
向下
向下
向下
x=-1
x=1
(0,0)
(-1,0)
(1,0)
平移时,一般按照“左加右减”的规律进行.例如,把二次函数y=ax2的图象沿x轴向左平移2个单位长度后,可以得到二次函数y=a(x+2)2的图象.把二次函数y=ax2的图象沿x轴向右平移2个单位长度后,可以得到二次函数y=a(x-2)2的图象.
一般地,抛物线y=a(x-h)2有如下性质:
①当a>0时,开口向上,当a<0时,开口向下.
②对称轴是直线x=h.
③顶点坐标是(h,0).
④ |a|越大,开口越小.
⑤二次函数y=a(x-h)2的图象可由二次函数y=ax2的图象经过左、右平移得到.当h>0时,二次函数y=a(x-h)2的图象可看成是由二次函数y=ax2的图象向右平移h个单位长度得到的.当h<0时,二次函数y=a(x-h)2的图象可看成是由二次函数y=ax2的图象向左平移|h|个单位长度得到的.
对于二次函数y=a(x-h)2(a≠0)图象上的两点A(x1,y1),B(x2,y2),当a>0时,若|x1-h|<|x2-h|,则y1< y2;当a<0时,若|x1-h|<|x2-h|,则y1>y2;对于任何a≠0时,若|x1-h|=|x2-h|,则y1= y2
二次函数y=ax2+k与y=a(x-h)2的性质.
表达式 a的 符号 开口 方向 对称轴 顶点坐标 增减性 最值
y=ax2+k
y= a(x-h)2
a>0
a<0
a>0
a<0
向上
向下
向上
向下
y轴
y轴
直线
x=h
直线
x=h
(0,k)
(0,k)
(h,0)
(h,0)
当x>0时,y随x的增大而增大
当x<0时, y随x的增大而减小
当x>0时, y随x的增大而减小
当x<0时, y随x的增大而增大
当x>h时, y随x的增大而增大
当x
当x
y最小值=k
当x=0时,
y最大值=k
当x=h时,
y最小值=0
当x=h时,
y最大值=0
1.下列抛物线的顶点坐标为(0,1)的是( )
A.y=x2+1 B.y=x2-1
C.y=(x+1)2 D.y=(x-1)2
A
2.抛物线y=-x2-1的开口方向和对称轴分
别是 ( )
A.向上,y轴 B.向下,y轴
C.向上,直线x=-1 D.向下,直线x=-1
B
3.在平面直角坐标系中,将二次函数y=2x2的图象向上平移2个单位长度,所得图象对应的函数解析式为 ( )
A.y=2x2+2 B.y=2x2-2
C.y=2(x+2)2 D.y=2(x-2)2
A
4.抛物线y=-3(x-2)2的开口向 ,对称轴是 .
下
直线x=2
5.抛物线y=-3x2向左平移3个单位长度,所得图象对应的函数解析式为 ,平移前后的图象形状 ,当x= 时,y有
最 值,为 .
y=-3(x+3)2
相同
-3
大
0
第二十二章 二次函数
22.1.3 二次函数y=a(x-h)2+k的图象和性质(2)
九年级数学上 新课标 [人]
讨论表格中前三个函数的内容
y=- x2 y=- x2-1 y =- (x+1)2 y=- (x+1)2-1
开口 方向
对称 轴
顶点 坐标
最值
增减 性
二次函数 的图象经过怎样的平移可以得到二次函数 和 的图象
在同一直角坐标系中,画出二次函数 和
的图象.
(1)二次函数
的图象与二次函数
的图象的相同点是 、 ;不同点是 、 .
(2)①抛物线
经过怎样的平移可以得到抛物线
?
②抛物线
经过怎样的平移可以得到抛物线
?
③抛物线
经过怎样的平移可以得到抛物线
?
总结结论:把抛物线
向左平移1个单位长度,再向下平移1个单位长度,就得到抛物线 .
(3)观察抛物线y=x2,y=(x-1)2,y=(x-1)2+1,你能用类比的方法判断这三条抛物线之间的位置关系吗
结论:这三条抛物线的开口方向和开口大小相同,顶点坐标不同,只有抛物线y=(x-1)2和抛物线y=(x-1)2+1的对称轴相同;抛物线y=x2向右平移1个单位长度,再向上平移1个单位长度,就得到抛物线y=(x-1)2+1.
(4)如果a>0,当x
抛物线y=a(x-h)2+k有如下特点:
(1)当a>0时,开口向上;当a<0时,开口向下.
(2)对称轴是直线x=h.
(3)顶点坐标是(h,k).
(5)将抛物线y=ax2先向上或向下平移|k|个单位长度(k>0时,向上平移;k<0时,向下平移),可得到抛物线y=ax2+k,然后再将抛物线y=ax2+k向左或向右平移|h|个单位长度(h>0时,向右平移;h<0时,向左平移),就可以得到抛物线y=a(x-h)2+k,当然也可以先左、右移,再上、下移.
要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1 m处达到最高,高度为3 m,水柱落地处离池中心3 m,水管应多长
解:如图所示,以水管与地面交点为原点,原点与水柱落地处所在直线为x轴,水管所在直线为y轴,建立直角坐标系.
点(1,3)是图中这段抛物线的顶点,因此可设这段抛物线对应的函数解析式是: y=a(x-1)2+3(0≤x≤3).
由这段抛物线经过点(3,0),可得0= a(3-1)2+3,解得 因此y=- (x-1)2+3(0≤x≤3).
当x= 0时,y=2.25.也就是说,水管应2.25 m长.
x
y
二次函数 表达式 a的符号 开口方向 对称轴 顶点坐标 增减性 最值
y=ax2+k a>0 向上 y轴 (0,k) 当x>0时,y随x的增大而增大 当x<0时,y随x的增大而减小 当x=0时,
y有最小值,
y最小值=k
a<0 向下 y轴 (0,k) 当x>0时,y随x的增大而减小 当x<0时,y随x的增大而增大 当x=0时,
y有最大值,
y最大值=k
y=a(x-h)2 a>0 向上 直线 x=h (h,0) 当x>h时,y随x的增大而增大 当x
y最小值=0
a<0 向下 直线 x=h (h,0) 当x>h时,y随x的增大而减小 当x
y最大值=0
y=a(x-h)2+k a>0 向上 直线 x=h (h,k) 当x>h时,y随x的增大而增大 当x
y最小值=k
a<0 向下 直线 x=h (h,k) 当x>h时,y随x的增大而减小 当x
y最大值=k
1.对于二次函数y=(x-1)2+2的图象,下列说法正确的是 ( )
A.开口向下 B.对称轴是直线x=-1
C.顶点坐标是(1,2) D.与x轴有两个交点
C
2.将二次函数y=x2的图象向右平移1个单位长度,再向上平移2个单位长度后,所得图象对应的函数解析式为 ( )
A.y=(x-1)2+2 B.y=(x+1)2+2
C.y=(x-1)2-2 D.y=(x+1)2-2
A
3.如图所示,在平面直角坐标系中,抛物线所表示的函数解析式为y=-2(x-h)2+k,则下列结论正确的是 ( )
A.h>0,k>0
B.h<0,k>0
C.h<0,k<0
D.h>0,k<0
A
4.二次函数y=(x-1)2+3的最小值为 .
3
5.抛物线 是由抛物线
先向 (填“左”或“右”)平移
个单位长度,再向 (填“上”或“下”)平移 个单位长度得到的.
左
3
下
2
谢 谢 观 看
同课章节目录
