人教版九年级数学22.1.4二次函数y=ax2+bx+c的图象和性质 课件(共33张PPT)
文档属性
| 名称 | 人教版九年级数学22.1.4二次函数y=ax2+bx+c的图象和性质 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 234.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 10:31:07 | ||
图片预览






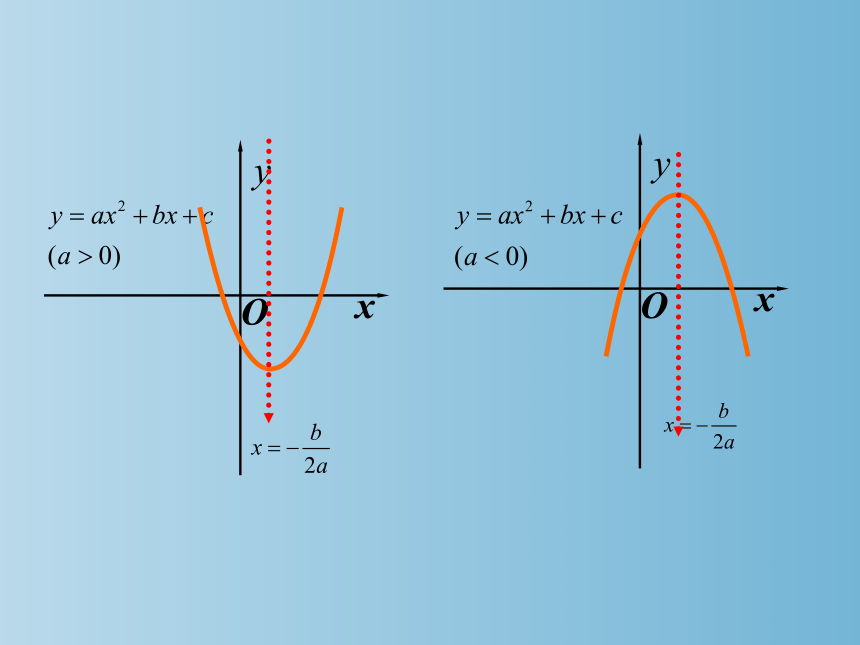




文档简介
(共33张PPT)
第二十二章 二次函数
22.1.4 二次函数y=ax2+bx+c的图象和性质(1)
九年级数学上 新课标 [人]
如图所示,在一场足球比赛中,九年级(1)班的球员李明从球门正前方10 m处起脚射门,球的运行路线可以近似看成是一条抛物线,当球飞行的水平距离是6 m时,球到达最高点,此时球距离地面3 m,已知球门高2.44 m,此球能否射进球门
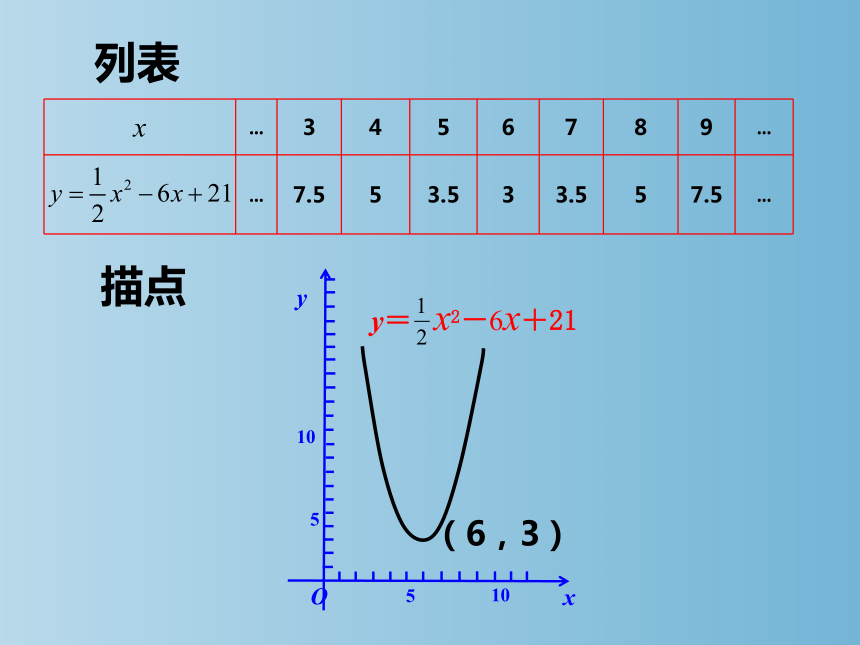
画出y= x2-6x+21的图象.
配方得:
y= x2-6x+21
=
(x-6)2+3
由此可知,抛物线 的顶点
是点(6,3),对称轴是直线 x=6.
y= x2-6x+21
探究1 二次函数 的图象
和性质
(1)
x … 3 4 5 6 7 8 9 …
… 7.5 5 3.5 3 3.5 5 7.5 …
列表
描点
O
y
x
5
10
5
10
(6,3)
y= x2-6x+21
O
y
x
5
10
5
10
20
15
x=6
·
(6,3)
·
·
y= x2-6x+21
当_____时y随x的增大而增大
当_____时y随x的增大而减小
x>6
x<6
提取二次项系数
配方:加上再减去一次项系数绝对值一半的平方
整理:前三项化为平方形式,后两项合并同类项
化简
一般地,对于二次函数y=ax +bx+c,我们可以利用配方法推导出它的对称轴和顶点坐标.
二次函数y=ax2+bx+c(a≠0)的图象和性质
抛物线的顶点式
二次函数y=ax +bx+c的图象是一条抛物线.
O
x
y
O
x
y
二次函数y=ax2+bx+c(a≠0)的性质
3.若抛物线与x轴有交点,则最好选取交点进行描点,特别是在画抛物线的草图的时候,应注意以下五点:开口方向、对称轴、顶点、与x轴的交点、与y轴的交点.
1.由于抛物线是轴对称图形,且对称轴经过抛物线的顶点,所以抛物线上对称点所连线段的垂直平分线是对称轴,对称轴与抛物线的交点是顶点.
2.在求二次函数y=ax2+bx+c(a≠0)的图象的对称轴及顶点坐标时,通常有两种方法:一是先将其配方,化y=ax2+bx+c为y=a(x-h)2+k的形式;二是直接利用公式求得答案.
1.二次函数y=-x2-4x-3图象的顶点坐标是 ( )
A.(2,-1) B.(-2,1)
C.(-2,-1) D.(2,1)
B
2.在二次函数y=-x2+2x+1的图象上,若y随x的 增大而增大,则x的取值范围是( )
A.x<1 B.x>1 C.x<-1 D.x>-1
A
3.已知抛物线y=-x2+4x-4,下列说法正确的是( )
A.当x=-2时,y有最大值
B.当x=2时,y有最大值
C.当x=-2时,y有最小值
D.当x=2时,y有最小值
B
4.若将二次函数y=x2-2x+3化为y=(x-h)2+k的形式,则 .
y=(x-1)2+2
5.二次函数y=x2+bx+3的图象的对称轴是直线x=-2,则b= .
解得b=4.故填4.
4
6.已知抛物线
(1)确定该抛物线的开口方向、顶点坐标和对称轴;
(2)当x取何值时,y随x的增大而增大 当x取何值时, y随x的增大而减小
解:(1)
该抛物线的开口向下,顶点坐标为 ,
,所以
对称轴是直线x=1.
(2)当x<1时, y随x的增大而增大,当x>1时,y随x的增大而减小.
第二十二章 二次函数
22.1.4 二次函数y=ax2+bx+c的图象和性质(2)
九年级数学上 新课标 [人]
(1)已知一个一次函数的图象与x轴交于点(3,0),与y轴交于点(0,6),求此一次函数的解析式.
(2)待定系数法求一次函数解析式的步骤是什么
设出解析式;根据条件列出方程或方程组;解方程(组)得出未知系数
(3)二次函数的解析式有哪几种形式
一般式:y=ax2+bx+c;顶点式:y=a(x-h)2+k;交点式:y=a(x-x1)(x-x2)
如果一个二次函数的图象经过
(-1,10),(1,4),(2,7)三点,能求出这个二次函数的解析式吗 如果能,求出这个二次函数的解析式.
一般式求二次函数解析式
(1)已知二次函数图象经过三点,有三个独立条件,所以可设二次函数的解析式为 .
(2)将三点坐标代入得方程组为 .
(3)解这个方程组得 . 所以所求的二次函数的解析式为 .
解:设所求二次函数的解析式为y=ax2+bx+c.
由已知函数图象经过(-1,10),(1,4),(2,7)三点,得关于a,b,c的三元一次方程组
解这个方程组,得a=2,b=-3,c=5.
∴所求的二次函数的解析式是y=2x2-3x+5.
顶点式求二次函数解析式
已知二次函数图象的顶点为(2,-4),且与y轴交于点(0,3),求这个二次函数的解析式.
引导:二次函数解析式的顶点式为 ,二次函数图象顶点为(2,-4)的二次函数的解析式可设为 ,点(0,3)在二次函数的图象上,所以点的坐标满足函数解析式,所以将点(0,3)代入得 ,解得 ,所以所求二次函数的解析式为 .
解:设所求二次函数的解析式为y=a(x-2)2-4.
已知函数图象经过点(0,3),所以4a-4=3.
解得
所以所求二次函数的解析式为
交点式求二次函数解析式
已知二次函数的图象与x轴交点的坐标为(-3,0),(1,0),且与y轴的交点为(0,-3),求这个二次函数的解析式.
引导:当二次函数图象与x轴的交点为(x1,0),(x2,0)时,可设所求函数解析式为y=a(x-x1)(x-x2),所以二次函数图象与x轴交点坐标为(-3,0),(1,0)时,可设函数解析式为 ,点(0,-3)在二次函数图象上,所以点的坐标满足函数解析式,所以将点(0,-3)代入得 ,解得 ,所以所求的二次函数的解析式为 .
解:设所求的二次函数的解析式为y=a(x+3)(x-1),
解得a=1.
所以所求的二次函数的解析式为y=(x+3)(x-1),即y=x2+2x-3.
由已知函数图象经过点(0,-3),所以-3a=-3,
归纳:
用交点式求二次函数解析式的一般方法和步骤.
当已知抛物线上任意三点时,通常设为一般式y=ax2+bx+c的形式;当已知抛物线的顶点与抛物线上另一点时,通常设为顶点式y=a(x-h)2+k的形式;当已知抛物线与x轴的交点或交点横坐标及抛物线上另一点时,通常设为交点式y=a(x-x1)·(x-x2).
有一个抛物线形的立交桥,这个桥拱的最大高度为16 m,跨度为40 m,现把它放在如图所示的直角坐标系里,若要在离跨度中心点M 5 m处垂直竖一根铁柱支撑这个拱顶,铁柱应取多长
∴0=a(40-20)2+16,
解:由题意,知抛物线的顶点坐标为(20,16),点B(40,0),
∴可设抛物线的解析式为y=a(x-20)2+16.
∵点B(40,0)在抛物线上,
∵竖铁柱的点为(15,0)或(25,0),
当x=15时,y= (15-20)2+16=15;
当x=25时,y= (25-20)2+16=15.
∴铁柱应取15 m长.
2.在选用不同的设法时,应具体问题具体分析,特别是当已知条件不是上述所列举的几种情形时,应灵活选用不同的方法来求解,以达到事半功倍的效果.
1.求二次函数解析式的几种方法之间是相互联系的,而不是孤立的,不同的函数解析式的设法是根据不同的已知条件来确定的.
1.已知二次函数的图象过(1,0),(2,0)和(0,2)三点,则该函数的解析式是 ( )
A.y=2x2+x+2 B.y=x2+3x+2D
C.y=x2-2x+3 D.y=x2-3x+2
D
2.过坐标原点,且顶点坐标是(1,-2)的抛物线的解析式为 .
y=2x2-4x
3.已知二次函数的图象与x轴交于点(2,0),(-1,0),与y轴交于点(0,-1),那么这个二次函数的解析式是 .
4.已知二次函数y=ax2+bx+c的图象过A(0,-5),B(5,0)两点,它的对称轴为直线x=2,那么这个二次函数的解析式是 .
y=x2-4x-5
5.已知二次函数图象的顶点坐标为(1,4),且经过点(-2,-5),求此二次函数的解析式.
谢 谢 观 看
第二十二章 二次函数
22.1.4 二次函数y=ax2+bx+c的图象和性质(1)
九年级数学上 新课标 [人]
如图所示,在一场足球比赛中,九年级(1)班的球员李明从球门正前方10 m处起脚射门,球的运行路线可以近似看成是一条抛物线,当球飞行的水平距离是6 m时,球到达最高点,此时球距离地面3 m,已知球门高2.44 m,此球能否射进球门
画出y= x2-6x+21的图象.
配方得:
y= x2-6x+21
=
(x-6)2+3
由此可知,抛物线 的顶点
是点(6,3),对称轴是直线 x=6.
y= x2-6x+21
探究1 二次函数 的图象
和性质
(1)
x … 3 4 5 6 7 8 9 …
… 7.5 5 3.5 3 3.5 5 7.5 …
列表
描点
O
y
x
5
10
5
10
(6,3)
y= x2-6x+21
O
y
x
5
10
5
10
20
15
x=6
·
(6,3)
·
·
y= x2-6x+21
当_____时y随x的增大而增大
当_____时y随x的增大而减小
x>6
x<6
提取二次项系数
配方:加上再减去一次项系数绝对值一半的平方
整理:前三项化为平方形式,后两项合并同类项
化简
一般地,对于二次函数y=ax +bx+c,我们可以利用配方法推导出它的对称轴和顶点坐标.
二次函数y=ax2+bx+c(a≠0)的图象和性质
抛物线的顶点式
二次函数y=ax +bx+c的图象是一条抛物线.
O
x
y
O
x
y
二次函数y=ax2+bx+c(a≠0)的性质
3.若抛物线与x轴有交点,则最好选取交点进行描点,特别是在画抛物线的草图的时候,应注意以下五点:开口方向、对称轴、顶点、与x轴的交点、与y轴的交点.
1.由于抛物线是轴对称图形,且对称轴经过抛物线的顶点,所以抛物线上对称点所连线段的垂直平分线是对称轴,对称轴与抛物线的交点是顶点.
2.在求二次函数y=ax2+bx+c(a≠0)的图象的对称轴及顶点坐标时,通常有两种方法:一是先将其配方,化y=ax2+bx+c为y=a(x-h)2+k的形式;二是直接利用公式求得答案.
1.二次函数y=-x2-4x-3图象的顶点坐标是 ( )
A.(2,-1) B.(-2,1)
C.(-2,-1) D.(2,1)
B
2.在二次函数y=-x2+2x+1的图象上,若y随x的 增大而增大,则x的取值范围是( )
A.x<1 B.x>1 C.x<-1 D.x>-1
A
3.已知抛物线y=-x2+4x-4,下列说法正确的是( )
A.当x=-2时,y有最大值
B.当x=2时,y有最大值
C.当x=-2时,y有最小值
D.当x=2时,y有最小值
B
4.若将二次函数y=x2-2x+3化为y=(x-h)2+k的形式,则 .
y=(x-1)2+2
5.二次函数y=x2+bx+3的图象的对称轴是直线x=-2,则b= .
解得b=4.故填4.
4
6.已知抛物线
(1)确定该抛物线的开口方向、顶点坐标和对称轴;
(2)当x取何值时,y随x的增大而增大 当x取何值时, y随x的增大而减小
解:(1)
该抛物线的开口向下,顶点坐标为 ,
,所以
对称轴是直线x=1.
(2)当x<1时, y随x的增大而增大,当x>1时,y随x的增大而减小.
第二十二章 二次函数
22.1.4 二次函数y=ax2+bx+c的图象和性质(2)
九年级数学上 新课标 [人]
(1)已知一个一次函数的图象与x轴交于点(3,0),与y轴交于点(0,6),求此一次函数的解析式.
(2)待定系数法求一次函数解析式的步骤是什么
设出解析式;根据条件列出方程或方程组;解方程(组)得出未知系数
(3)二次函数的解析式有哪几种形式
一般式:y=ax2+bx+c;顶点式:y=a(x-h)2+k;交点式:y=a(x-x1)(x-x2)
如果一个二次函数的图象经过
(-1,10),(1,4),(2,7)三点,能求出这个二次函数的解析式吗 如果能,求出这个二次函数的解析式.
一般式求二次函数解析式
(1)已知二次函数图象经过三点,有三个独立条件,所以可设二次函数的解析式为 .
(2)将三点坐标代入得方程组为 .
(3)解这个方程组得 . 所以所求的二次函数的解析式为 .
解:设所求二次函数的解析式为y=ax2+bx+c.
由已知函数图象经过(-1,10),(1,4),(2,7)三点,得关于a,b,c的三元一次方程组
解这个方程组,得a=2,b=-3,c=5.
∴所求的二次函数的解析式是y=2x2-3x+5.
顶点式求二次函数解析式
已知二次函数图象的顶点为(2,-4),且与y轴交于点(0,3),求这个二次函数的解析式.
引导:二次函数解析式的顶点式为 ,二次函数图象顶点为(2,-4)的二次函数的解析式可设为 ,点(0,3)在二次函数的图象上,所以点的坐标满足函数解析式,所以将点(0,3)代入得 ,解得 ,所以所求二次函数的解析式为 .
解:设所求二次函数的解析式为y=a(x-2)2-4.
已知函数图象经过点(0,3),所以4a-4=3.
解得
所以所求二次函数的解析式为
交点式求二次函数解析式
已知二次函数的图象与x轴交点的坐标为(-3,0),(1,0),且与y轴的交点为(0,-3),求这个二次函数的解析式.
引导:当二次函数图象与x轴的交点为(x1,0),(x2,0)时,可设所求函数解析式为y=a(x-x1)(x-x2),所以二次函数图象与x轴交点坐标为(-3,0),(1,0)时,可设函数解析式为 ,点(0,-3)在二次函数图象上,所以点的坐标满足函数解析式,所以将点(0,-3)代入得 ,解得 ,所以所求的二次函数的解析式为 .
解:设所求的二次函数的解析式为y=a(x+3)(x-1),
解得a=1.
所以所求的二次函数的解析式为y=(x+3)(x-1),即y=x2+2x-3.
由已知函数图象经过点(0,-3),所以-3a=-3,
归纳:
用交点式求二次函数解析式的一般方法和步骤.
当已知抛物线上任意三点时,通常设为一般式y=ax2+bx+c的形式;当已知抛物线的顶点与抛物线上另一点时,通常设为顶点式y=a(x-h)2+k的形式;当已知抛物线与x轴的交点或交点横坐标及抛物线上另一点时,通常设为交点式y=a(x-x1)·(x-x2).
有一个抛物线形的立交桥,这个桥拱的最大高度为16 m,跨度为40 m,现把它放在如图所示的直角坐标系里,若要在离跨度中心点M 5 m处垂直竖一根铁柱支撑这个拱顶,铁柱应取多长
∴0=a(40-20)2+16,
解:由题意,知抛物线的顶点坐标为(20,16),点B(40,0),
∴可设抛物线的解析式为y=a(x-20)2+16.
∵点B(40,0)在抛物线上,
∵竖铁柱的点为(15,0)或(25,0),
当x=15时,y= (15-20)2+16=15;
当x=25时,y= (25-20)2+16=15.
∴铁柱应取15 m长.
2.在选用不同的设法时,应具体问题具体分析,特别是当已知条件不是上述所列举的几种情形时,应灵活选用不同的方法来求解,以达到事半功倍的效果.
1.求二次函数解析式的几种方法之间是相互联系的,而不是孤立的,不同的函数解析式的设法是根据不同的已知条件来确定的.
1.已知二次函数的图象过(1,0),(2,0)和(0,2)三点,则该函数的解析式是 ( )
A.y=2x2+x+2 B.y=x2+3x+2D
C.y=x2-2x+3 D.y=x2-3x+2
D
2.过坐标原点,且顶点坐标是(1,-2)的抛物线的解析式为 .
y=2x2-4x
3.已知二次函数的图象与x轴交于点(2,0),(-1,0),与y轴交于点(0,-1),那么这个二次函数的解析式是 .
4.已知二次函数y=ax2+bx+c的图象过A(0,-5),B(5,0)两点,它的对称轴为直线x=2,那么这个二次函数的解析式是 .
y=x2-4x-5
5.已知二次函数图象的顶点坐标为(1,4),且经过点(-2,-5),求此二次函数的解析式.
谢 谢 观 看
同课章节目录
