人教版九年级数学上册 24.1.4圆周角课件 (共30张PPT)
文档属性
| 名称 | 人教版九年级数学上册 24.1.4圆周角课件 (共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 596.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 10:31:15 | ||
图片预览







文档简介
(共30张PPT)
第二十四章 圆
24.1.4 圆周角(第1课时)
九年级数学上 新课标 [人]
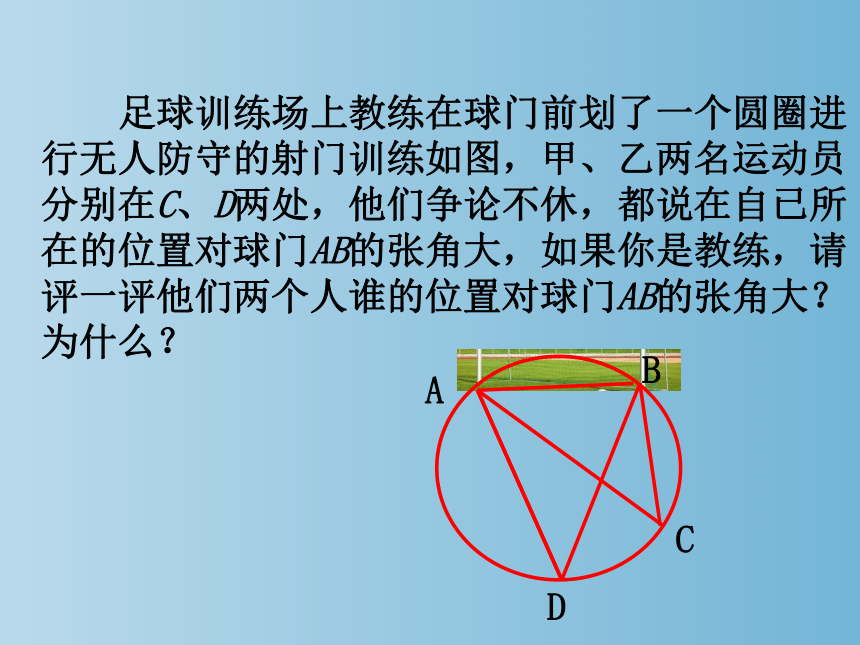
足球训练场上教练在球门前划了一个圆圈进行无人防守的射门训练如图,甲、乙两名运动员分别在C、D两处,他们争论不休,都说在自已所在的位置对球门AB的张角大,如果你是教练,请评一评他们两个人谁的位置对球门AB的张角大?为什么?
A
B
D
C
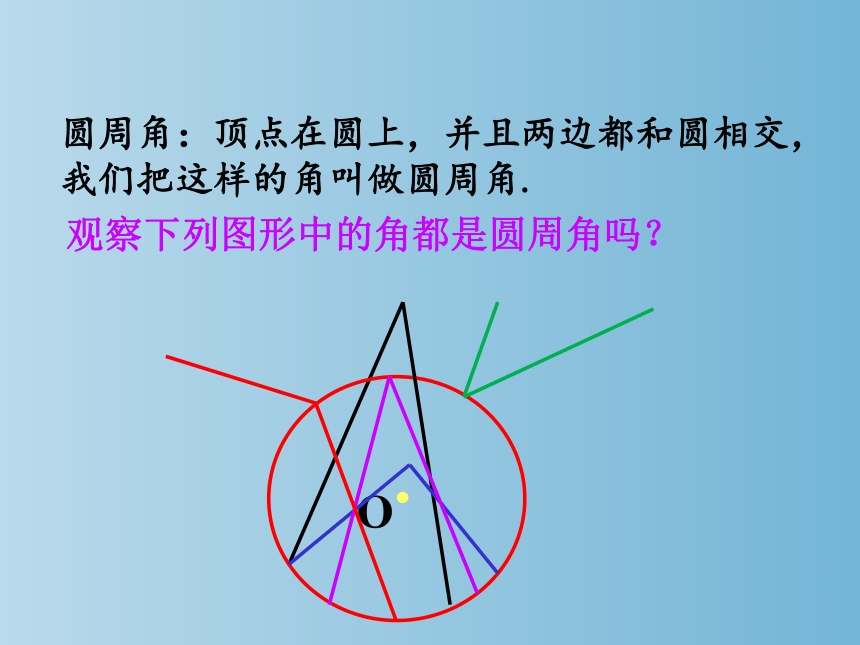
圆周角:顶点在圆上,并且两边都和圆相交,我们把这样的角叫做圆周角.
观察下列图形中的角都是圆周角吗?
O
动手操作:
1.画⊙O,在⊙O上任意画弧AB,分别画出弧AB所对的圆心角和圆周角.
2.你能画出几个弧AB所对的圆心角和圆周角?
3.分别测量所画圆心角和圆周角的度数,它们之间有什么关系?
思考:
1.在圆上任取一个圆周角,观察圆心与圆周角的位置关系有几种情况?
2.当圆心在圆周角的一边上时,如何证明所发现的结论?
3.当圆心不在圆周角的一边上时,如何证明所发现的结论?
4.归纳你用到的数学方法和得出的结论.
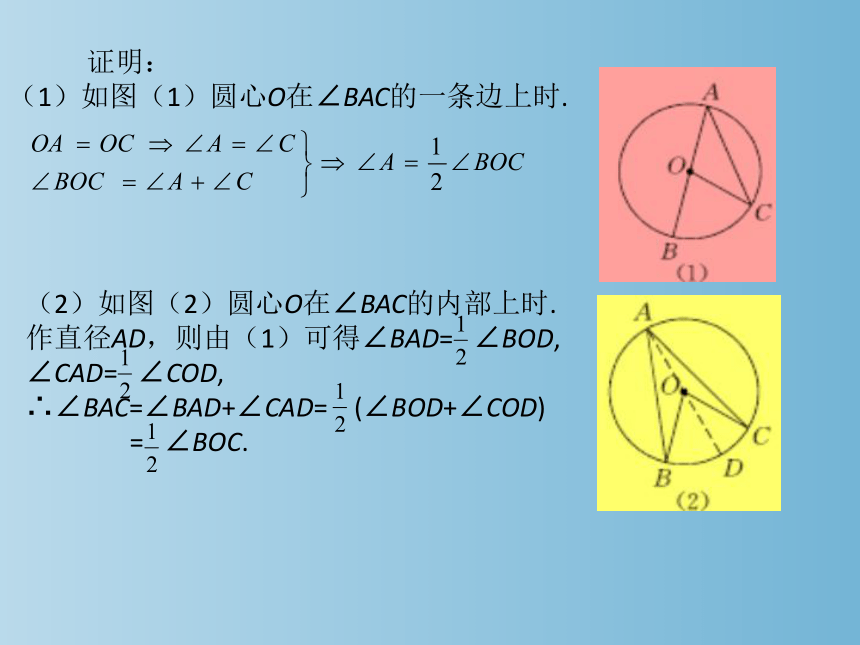
证明:
(1)如图(1)圆心O在∠BAC的一条边上时.
(2)如图(2)圆心O在∠BAC的内部上时.
作直径AD,则由(1)可得∠BAD= ∠BOD,
∠CAD= ∠COD,
∴∠BAC=∠BAD+∠CAD= (∠BOD+∠COD)
= ∠BOC.
证明:
(3)如图(3) ,圆心O在∠BAC的外部上时.
作直径AD,则由(1)可得∠CAD= ∠COD,
∠BAD= ∠BOD,
∴∠BAC=∠CAD-∠BAD= (∠COD-∠BOD)= ∠B0C.
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
数学思想方法:分类思想、化归思想、由特殊到一般的数学方法.
思考:
1.同弧所对的圆周角是否相等?
2.如果改为等弧,那么所对的圆周角还是否相等?为什么?
3.半圆(或直径)所对的圆周角是多少度?
4.90°的圆周角所对的弦是什么?
·
A
B
C1
O
C2
C3
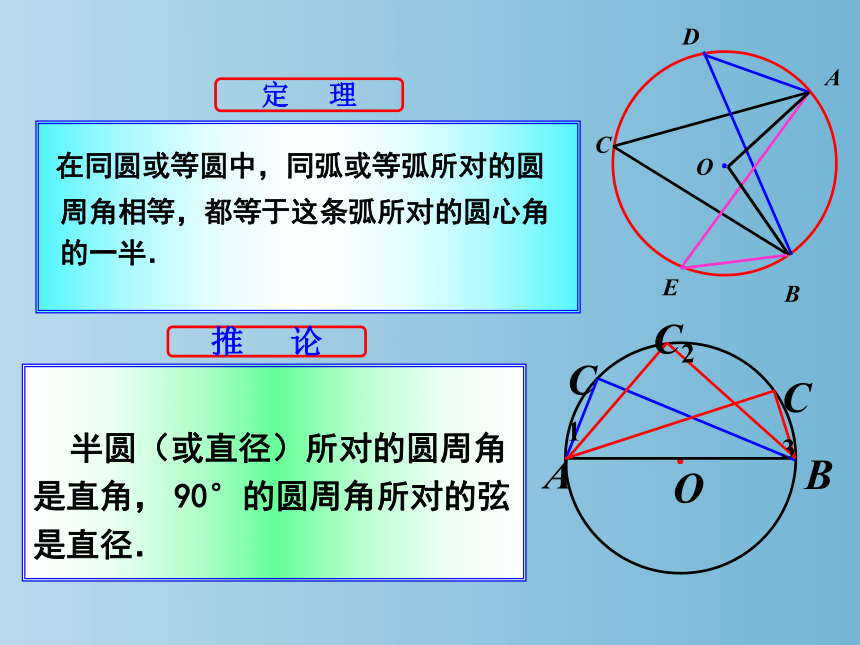
在同圆或等圆中,同弧或等弧所对的圆
周角相等,都等于这条弧所对的圆心角
的一半.
定 理
半圆(或直径)所对的圆周角是直角, 90°的圆周角所对的弦是直径.
推 论
·
A
B
C
D
E
O
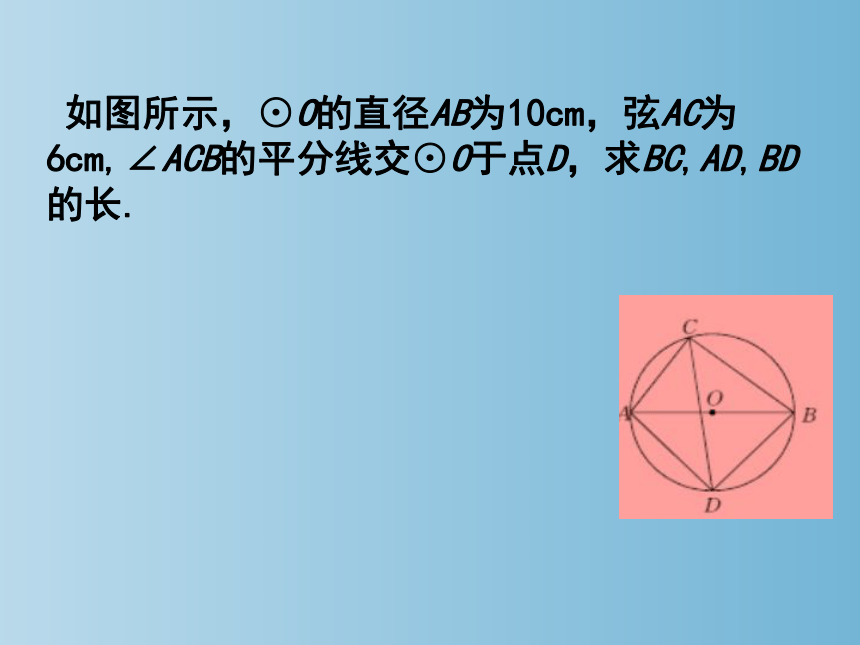
如图所示,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,求BC,AD,BD的长.
又在Rt△ABD中,AD2+BD2=AB2,
·
A
B
C
D
O
解:∵AB是直径,
∴ ∠ACB= ∠ADB=90°.
在Rt△ABC中,
∵CD平分∠ACB,
∴AD=BD.
10
6
)
)
8
小结
1.圆周角的概念:顶点在圆上,并且两边都与圆相交,我们把这样的角叫做圆周角.
2.圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
3.推论:同弧或等弧所对的圆周角相等;半圆(或直径)所对的圆周角是直角,90°圆周角所对的弦是直径.
4.本节课数学思想方法:分类思想、化归思想、有特殊到一般的数学方法.
1.如图,点A、B、C都在⊙O上,若∠C=34°,则∠AOB的度数为( )
A.34° B.56° C.60° D.68°
O
C
B
A
D
2.如图,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于( )
A.80° B.50° C.40° D.20°
D
3.如图,点A、B、C、D在⊙O上,若∠C=60°,则∠D=______,∠AOB=______.
60°
120°
4.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?为什么?
第二十四章 圆
24.1.4 圆周角(第2课时)
九年级数学上 新课标 [人]
在这个圆形人工湖边上造4个休息厅,(即A、B、C、D),用仪器测得圆周角∠A=75°,∠B=65°,能求出另两个角∠C和∠D的度数吗?需要哪些数据可以求该圆形人工湖的直径?
A
B
C
D
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
如图中的四边形ABCD叫做⊙O的内接四边形,而⊙O叫做四边形ABCD的外接圆.
圆内接四边形的4个角之间有什么关系?
1.在圆内画圆不同的内接四边形ABCD,用量角器分别度量一组对角的和.
2.观察所得数据,你发现了什么?
3.作出猜想:圆内接四边形的对角互补.
4.你能证明自己的猜想吗?
已知:四边形ABCD内接于⊙O.
求证:∠A+∠C=180°,∠B+∠D=180°.
∴∠A+∠C= =180°.
证明:如图所示,连接OB,OD.
∵∠A所对的弧为 ,
∠C所对的弧为 ,
又∵ 和 所对的圆心角的和是周角,
同理∠B+∠D=180°.
圆内接四边形的性质:圆内接四边形的对角互补.
1.圆内接四边形的外角等于它的内对角.
2.圆内接四边形性质是解决有关角的计算和证明常用的结论.
1.圆内接四边形的有关概念: 如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
2.圆内接四边形的性质:圆内接四边形的对角互补.
小结
1.若ABCD为圆内接四边形,则下列 哪个选项可能成立( )
A.∠A∶∠B∶∠C∶∠D = 1∶2∶3∶4 B.∠A∶∠B∶∠C∶∠D = 2∶1∶3∶4
C.∠A∶∠B∶∠C∶∠D = 3∶2∶1∶4 D.∠A∶∠B∶∠C∶∠D = 4∶3∶3∶2
B
2.如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于( ).
A.69° B.42° C.48° D.38°
A
3.已知如图,在圆内接四边形ABCD中,∠B=30°,则∠D=_____.
150°
4.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,∠BCD=120°,BC=CD.
(1)求证:CD∥AB;
(2)求S△ACD:S△ABC的值.
解:(1)∵AB是⊙O的直径,∴∠ACB=90°,
∵∠BCD=120°,
∴∠ACD=30°,∠DAB=180°-∠BCD=60°,
∵BC=CD,∴弧BC=弧CD,
∴∠DAC=∠BAC= ×60°=30°,
∴∠B=90°-∠BAC=60°,∴∠B+∠BCD=180°,
∴CD∥AB
(2)连结OA、OB,∵∠DOC=2∠DAC=60°,
∴△ODC为等边三角形,而∠B=60°,
∴△OBC为等边三角形,∵AB∥CD,
∴S△ADC=S△ODC,而S△OBC=S△ODC,S△ABC=2S△OBC,
∴S△ACD:S△ABC=1:2.
谢 谢 观 看
第二十四章 圆
24.1.4 圆周角(第1课时)
九年级数学上 新课标 [人]
足球训练场上教练在球门前划了一个圆圈进行无人防守的射门训练如图,甲、乙两名运动员分别在C、D两处,他们争论不休,都说在自已所在的位置对球门AB的张角大,如果你是教练,请评一评他们两个人谁的位置对球门AB的张角大?为什么?
A
B
D
C
圆周角:顶点在圆上,并且两边都和圆相交,我们把这样的角叫做圆周角.
观察下列图形中的角都是圆周角吗?
O
动手操作:
1.画⊙O,在⊙O上任意画弧AB,分别画出弧AB所对的圆心角和圆周角.
2.你能画出几个弧AB所对的圆心角和圆周角?
3.分别测量所画圆心角和圆周角的度数,它们之间有什么关系?
思考:
1.在圆上任取一个圆周角,观察圆心与圆周角的位置关系有几种情况?
2.当圆心在圆周角的一边上时,如何证明所发现的结论?
3.当圆心不在圆周角的一边上时,如何证明所发现的结论?
4.归纳你用到的数学方法和得出的结论.
证明:
(1)如图(1)圆心O在∠BAC的一条边上时.
(2)如图(2)圆心O在∠BAC的内部上时.
作直径AD,则由(1)可得∠BAD= ∠BOD,
∠CAD= ∠COD,
∴∠BAC=∠BAD+∠CAD= (∠BOD+∠COD)
= ∠BOC.
证明:
(3)如图(3) ,圆心O在∠BAC的外部上时.
作直径AD,则由(1)可得∠CAD= ∠COD,
∠BAD= ∠BOD,
∴∠BAC=∠CAD-∠BAD= (∠COD-∠BOD)= ∠B0C.
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
数学思想方法:分类思想、化归思想、由特殊到一般的数学方法.
思考:
1.同弧所对的圆周角是否相等?
2.如果改为等弧,那么所对的圆周角还是否相等?为什么?
3.半圆(或直径)所对的圆周角是多少度?
4.90°的圆周角所对的弦是什么?
·
A
B
C1
O
C2
C3
在同圆或等圆中,同弧或等弧所对的圆
周角相等,都等于这条弧所对的圆心角
的一半.
定 理
半圆(或直径)所对的圆周角是直角, 90°的圆周角所对的弦是直径.
推 论
·
A
B
C
D
E
O
如图所示,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,求BC,AD,BD的长.
又在Rt△ABD中,AD2+BD2=AB2,
·
A
B
C
D
O
解:∵AB是直径,
∴ ∠ACB= ∠ADB=90°.
在Rt△ABC中,
∵CD平分∠ACB,
∴AD=BD.
10
6
)
)
8
小结
1.圆周角的概念:顶点在圆上,并且两边都与圆相交,我们把这样的角叫做圆周角.
2.圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
3.推论:同弧或等弧所对的圆周角相等;半圆(或直径)所对的圆周角是直角,90°圆周角所对的弦是直径.
4.本节课数学思想方法:分类思想、化归思想、有特殊到一般的数学方法.
1.如图,点A、B、C都在⊙O上,若∠C=34°,则∠AOB的度数为( )
A.34° B.56° C.60° D.68°
O
C
B
A
D
2.如图,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于( )
A.80° B.50° C.40° D.20°
D
3.如图,点A、B、C、D在⊙O上,若∠C=60°,则∠D=______,∠AOB=______.
60°
120°
4.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?为什么?
第二十四章 圆
24.1.4 圆周角(第2课时)
九年级数学上 新课标 [人]
在这个圆形人工湖边上造4个休息厅,(即A、B、C、D),用仪器测得圆周角∠A=75°,∠B=65°,能求出另两个角∠C和∠D的度数吗?需要哪些数据可以求该圆形人工湖的直径?
A
B
C
D
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
如图中的四边形ABCD叫做⊙O的内接四边形,而⊙O叫做四边形ABCD的外接圆.
圆内接四边形的4个角之间有什么关系?
1.在圆内画圆不同的内接四边形ABCD,用量角器分别度量一组对角的和.
2.观察所得数据,你发现了什么?
3.作出猜想:圆内接四边形的对角互补.
4.你能证明自己的猜想吗?
已知:四边形ABCD内接于⊙O.
求证:∠A+∠C=180°,∠B+∠D=180°.
∴∠A+∠C= =180°.
证明:如图所示,连接OB,OD.
∵∠A所对的弧为 ,
∠C所对的弧为 ,
又∵ 和 所对的圆心角的和是周角,
同理∠B+∠D=180°.
圆内接四边形的性质:圆内接四边形的对角互补.
1.圆内接四边形的外角等于它的内对角.
2.圆内接四边形性质是解决有关角的计算和证明常用的结论.
1.圆内接四边形的有关概念: 如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
2.圆内接四边形的性质:圆内接四边形的对角互补.
小结
1.若ABCD为圆内接四边形,则下列 哪个选项可能成立( )
A.∠A∶∠B∶∠C∶∠D = 1∶2∶3∶4 B.∠A∶∠B∶∠C∶∠D = 2∶1∶3∶4
C.∠A∶∠B∶∠C∶∠D = 3∶2∶1∶4 D.∠A∶∠B∶∠C∶∠D = 4∶3∶3∶2
B
2.如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于( ).
A.69° B.42° C.48° D.38°
A
3.已知如图,在圆内接四边形ABCD中,∠B=30°,则∠D=_____.
150°
4.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,∠BCD=120°,BC=CD.
(1)求证:CD∥AB;
(2)求S△ACD:S△ABC的值.
解:(1)∵AB是⊙O的直径,∴∠ACB=90°,
∵∠BCD=120°,
∴∠ACD=30°,∠DAB=180°-∠BCD=60°,
∵BC=CD,∴弧BC=弧CD,
∴∠DAC=∠BAC= ×60°=30°,
∴∠B=90°-∠BAC=60°,∴∠B+∠BCD=180°,
∴CD∥AB
(2)连结OA、OB,∵∠DOC=2∠DAC=60°,
∴△ODC为等边三角形,而∠B=60°,
∴△OBC为等边三角形,∵AB∥CD,
∴S△ADC=S△ODC,而S△OBC=S△ODC,S△ABC=2S△OBC,
∴S△ACD:S△ABC=1:2.
谢 谢 观 看
同课章节目录
