人教版九年级数学上册 24.2.2直线和圆的位置关系课件 (共41张PPT)
文档属性
| 名称 | 人教版九年级数学上册 24.2.2直线和圆的位置关系课件 (共41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 256.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 10:32:06 | ||
图片预览










文档简介
(共41张PPT)
第二十四章 圆
24.2.2直线和圆的位置关系第1课时
九年级数学上 新课标 [人]
“大漠孤烟直,长河落日圆”是唐朝诗人王维的诗句,它描述了黄昏日落时分塞外特有的景象.如图,如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?
直线和圆的三种位置关系:
相交:直线和圆有两个公共点,这时我们就说这条直线和圆相交,这条直线叫做圆的割线.
相切:直线和圆只有一个公共点,这时我们就说这条直线和圆相切,这条直线叫做圆的切线,这个点叫作切点.
相离:直线和圆没有公共点,这时我们就说这条直线和圆相离.
1.动手操作:画出直线和圆的三种位置关系,并作出圆心到直线的距离.
2.思考一:设⊙O的半径为r,圆心到直线的距离为d.你能仿照点和圆的位置关系中,点到圆心的距离d与半径r之间的数量关系,用圆心到直线的距离d和圆半径r的数量关系,来揭示直线和圆的三种位置关系?
如果⊙O的半径为r,圆心O到直线l的距离为d,那么
直线l与⊙O相交 d直线l与⊙O相切 d=r;
直线l与⊙O相离 d>r.
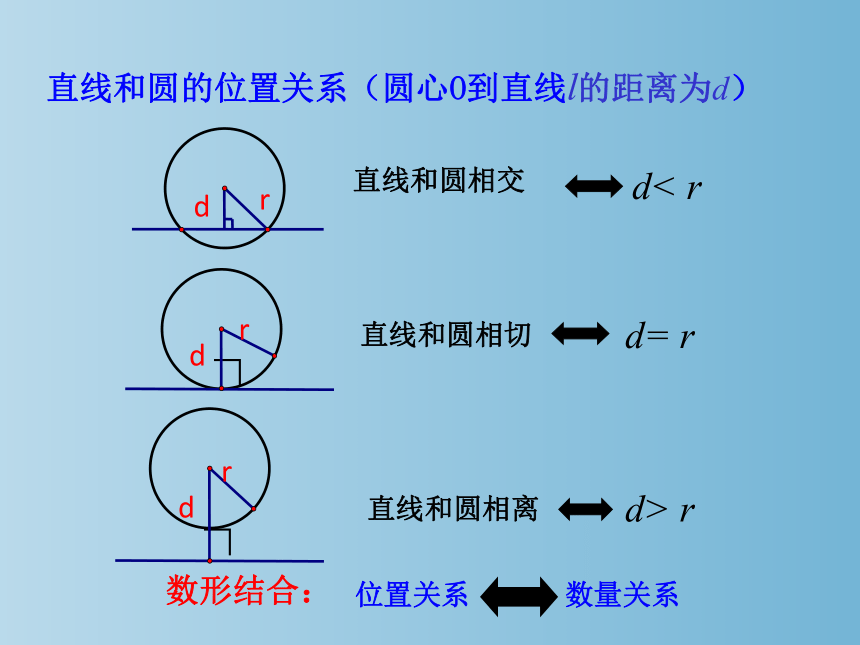
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
r
d
∟
r
d
∟
r
d
数形结合:
位置关系
数量关系
直线和圆的位置关系(圆心O到直线l的距离为d)
.
l
┐
d
r
.
l
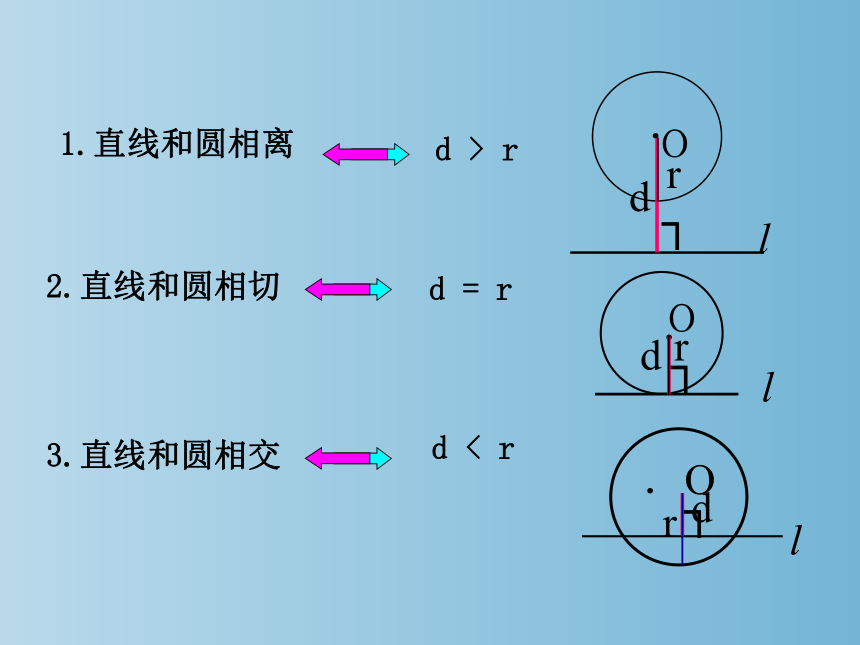
2.直线和圆相切
┐
d
r
d = r
.O
l
3.直线和圆相交
d < r
d
┐
r
1.直线和圆相离
d > r
O
O
小结:1、直线与圆的位置关系:
0
d>r
1
d=r
切点
切线
2
d交点
割线
.O
l
d
r
┐
┐
.o
l
d
r
.O
l
d
┐
r
.
A
C
B
.
.
相离
相切
相交
切线的判定
如图所示,在⊙O中,经过半径OA的外端点A作直线l ⊥OA,则圆心O到直线l的距离是多少?直线l与⊙O有什么位置关系?
5.你能举出生活中直线与圆相切的实例吗?
1.圆心O到直线l的距离是 ,与☉O的半径的大小关系是 ,所以直线l与☉O的位置关系是 .
2.该命题的已知条件是 ,结论是 ,用语言叙述该命题为 .
3.已知一个圆和圆上的一点,如何过这个点画出圆的切线
(过该点作半径的垂线.)
4.如何证明一条直线是圆的切线?
切线的判定定理:
经过半径的外端并且垂直于这条半径的直线是圆的切线.
切线的性质
切线的判定定理的逆命题是什么?你能用反证法证明吗?
已知:如图,如果直线l是⊙O的切线,切点为A.
求证:半径OA与直线l垂直.
证明:假设OA与l不垂直,过点O作OM⊥l,垂足为M,根据垂线段最短的性质,有
OM<OA,这说明圆心O到直线l的距离小于半径OA,于是直线l与圆相交,而这与直线l是⊙O的切线矛盾.因此,半径OA与直线l垂直.
切线的性质定理:
圆的切线垂直于过切点的半径.
例1 如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.
求证:AC是⊙O的切线.
证明:如图,过点O作OE⊥AC,垂足为E,连接OD,OA.
∵⊙O与AB相切于点D,∴OD⊥AB,
又△ABC为等腰三角形,O是底边BC的中点,∴AO是∠BAC的平分线.
∴OE=OD,即OE是⊙O的半径,
∴AC与⊙O相切.
1.直线和圆的位置关系:
如果⊙O的半径为r,圆心O到直线l的距离为d,那么直线l与⊙O相交 dr.
2.切线的判定定理:
经过半径的外端并且垂直于这条半径的直线是圆的切线.
小结
3.切线的性质定理:
圆的切线垂直于过切点的半径.
4.运用切线的性质和判定定理时常作的辅助线:
连接半径、过圆心作直线的垂线.
1.已知⊙O的半径是6,点O到直线l的距离为5,则直线l与⊙O的位置关系是( )
A.相离 B.相切 C.相交 D.无法判断
C
A
2.如图,若⊙的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D,且⊙O的半径为2,则CD的长为( )
A. B. C.2 D. 4
3.如图,PA是⊙O的切线,切点为A,PA= ,
∠APO=30°,则⊙O的半径长为______.
2
4.如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交⊙O于点D.
(1)BD是⊙O的切线吗?为什么?
(2)若AC=10,求线段BC的长度.
解:
(1)BD是⊙O的切线.
证明:∵∠BAD=∠B=30°,
∴∠ADB=180°-30°-30°=120°,∵AO=DO,∴∠A=∠ADO=30°,
∴∠ODB=120°-30°=90°,∴BD是⊙O的切线;
(2)解:∵AC=10,∴CO=5,∴DO=5,∵∠B=30°,∴BO=2DO=10,
在Rt△OBD中:BD= .
第二十四章 圆
24.2.2直线和圆的位置关系(第2课时)
九年级数学上 新课标 [人]
如图所示是一张三角形的铁皮,如何在它的上面剪下一块圆形的用料,并且使圆的面积尽可能的大呢?
1.什么是圆的切线长?
2.过圆外一点可以引圆的几条切线?
3.切线和切线长的区别是什么?
1. 经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长.
如图,过圆外一点P有圆的两条切线PA、PB,则线段PA、PB的长是⊙O的切线长.
2.切线和切线长的区别:
切线是直线,无法度量;
切线长是切线上一条线段的长,
即圆外一点与切点之间的距离,可以度量.
1.在纸上画⊙O,过圆上点A作⊙O的切线PA.
2.连接PO,沿着直线PO将纸对折,设圆上与点A重合的点为点B.
3.连接PB.
1.PB是⊙O的切线吗?
2.图中的PA与PB、∠APO与∠BPO有什么关系?
3.由圆的对称性你能说明你的结论是正确的吗?
4.分析已知和求证,写出逻辑证明过程.
已知:如上图,已知PA、PB是⊙O的两条切线,切点分别为A,B.
求证:PA=PB,∠OPA=∠OPB.
证明:连接OA、OB.
∵PA和PB是⊙O的两条切线,
∴OA⊥AP,OB⊥BP,
又OA=OB,OP=OP,∴Rt△AOP≌Rt△BOP,
∴PA=PB,∠APO=∠BPO.
如图是一块三角形的铁皮,如何在它上面截下一块圆形的用料,并且使截下来的圆与三角形的三条边都相切
A
B
C
1.刚才所画的三角形三条角平分线的交点有什么性质?
2.作圆的关键是什么?
3.如果我们已经作出圆,圆心满足什么条件?
4.找到圆心后,如何确定圆的半径?
内切圆:与三角形各边都相切的圆叫三角形的内切圆.内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
如图所示,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9,BC=14,CA=13.求AF、BD、CE的长.
观察图形和已知,⊙O与BC,CA,AB
分别相切于点D,E,F,,
则根据切线长定理可得 ,
又因为AB=9,BC=14,CA=13,
所以有等量关系 ,
, .
根据等量关系,考虑方程思想解答,所以设 ,根据等量关系可以用未知数表示线段 ,所以可列方程 ,解方程可得.
由BD+CD=BC,可得(13-x)+(9-x)=14.
解:设AF=x,则AE=x,CD=CE=AC-AE=13-x,
BD=BF=AB-AF=9-x.
解得x=4.
因此AF=4,BD=5,CE=9.
1.切线长定义:
经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长.
2.切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
小结
3.三角形的内切圆:
与三角形各边都相切的圆叫三角形的内切圆.内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
小结
1.如图所示,从圆外一点P引⊙O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=10,则弦AB的长( )
A.5 B. C.10 D.
C
C
2.从圆外一点向半径为9的圆作切线,已知切线长为18,从这点到圆的最短距离为( ).
A. B.9( ) C.9( ) D.9
3.如图,PA、PB分别切⊙O于A、B,并与⊙O的切线分别相交于C、D,已知PA=7cm,则△PCD的周长等于_________.
14cm
4.如图,AB,BC,CD分别与⊙O相切于E,F,G.且AB∥CD.BO=6cm,CO=8cm.
求证:BO⊥CO;
证明:∵AB∥CD,∴∠ABC+∠BCD=180°,∵AB、BC、CD分别与⊙O相切于E、F、G,
∴∠OBC= ∠ABC,∠OCB= ∠DCB,
∴∠OBC+∠OCB=(∠ABC+∠DCB)=×180°=90°,∴∠BOC=90°,∴BO⊥CO.
谢 谢 观 看
第二十四章 圆
24.2.2直线和圆的位置关系第1课时
九年级数学上 新课标 [人]
“大漠孤烟直,长河落日圆”是唐朝诗人王维的诗句,它描述了黄昏日落时分塞外特有的景象.如图,如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?
直线和圆的三种位置关系:
相交:直线和圆有两个公共点,这时我们就说这条直线和圆相交,这条直线叫做圆的割线.
相切:直线和圆只有一个公共点,这时我们就说这条直线和圆相切,这条直线叫做圆的切线,这个点叫作切点.
相离:直线和圆没有公共点,这时我们就说这条直线和圆相离.
1.动手操作:画出直线和圆的三种位置关系,并作出圆心到直线的距离.
2.思考一:设⊙O的半径为r,圆心到直线的距离为d.你能仿照点和圆的位置关系中,点到圆心的距离d与半径r之间的数量关系,用圆心到直线的距离d和圆半径r的数量关系,来揭示直线和圆的三种位置关系?
如果⊙O的半径为r,圆心O到直线l的距离为d,那么
直线l与⊙O相交 d
直线l与⊙O相离 d>r.
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
r
d
∟
r
d
∟
r
d
数形结合:
位置关系
数量关系
直线和圆的位置关系(圆心O到直线l的距离为d)
.
l
┐
d
r
.
l
2.直线和圆相切
┐
d
r
d = r
.O
l
3.直线和圆相交
d < r
d
┐
r
1.直线和圆相离
d > r
O
O
小结:1、直线与圆的位置关系:
0
d>r
1
d=r
切点
切线
2
d
割线
.O
l
d
r
┐
┐
.o
l
d
r
.O
l
d
┐
r
.
A
C
B
.
.
相离
相切
相交
切线的判定
如图所示,在⊙O中,经过半径OA的外端点A作直线l ⊥OA,则圆心O到直线l的距离是多少?直线l与⊙O有什么位置关系?
5.你能举出生活中直线与圆相切的实例吗?
1.圆心O到直线l的距离是 ,与☉O的半径的大小关系是 ,所以直线l与☉O的位置关系是 .
2.该命题的已知条件是 ,结论是 ,用语言叙述该命题为 .
3.已知一个圆和圆上的一点,如何过这个点画出圆的切线
(过该点作半径的垂线.)
4.如何证明一条直线是圆的切线?
切线的判定定理:
经过半径的外端并且垂直于这条半径的直线是圆的切线.
切线的性质
切线的判定定理的逆命题是什么?你能用反证法证明吗?
已知:如图,如果直线l是⊙O的切线,切点为A.
求证:半径OA与直线l垂直.
证明:假设OA与l不垂直,过点O作OM⊥l,垂足为M,根据垂线段最短的性质,有
OM<OA,这说明圆心O到直线l的距离小于半径OA,于是直线l与圆相交,而这与直线l是⊙O的切线矛盾.因此,半径OA与直线l垂直.
切线的性质定理:
圆的切线垂直于过切点的半径.
例1 如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.
求证:AC是⊙O的切线.
证明:如图,过点O作OE⊥AC,垂足为E,连接OD,OA.
∵⊙O与AB相切于点D,∴OD⊥AB,
又△ABC为等腰三角形,O是底边BC的中点,∴AO是∠BAC的平分线.
∴OE=OD,即OE是⊙O的半径,
∴AC与⊙O相切.
1.直线和圆的位置关系:
如果⊙O的半径为r,圆心O到直线l的距离为d,那么直线l与⊙O相交 d
2.切线的判定定理:
经过半径的外端并且垂直于这条半径的直线是圆的切线.
小结
3.切线的性质定理:
圆的切线垂直于过切点的半径.
4.运用切线的性质和判定定理时常作的辅助线:
连接半径、过圆心作直线的垂线.
1.已知⊙O的半径是6,点O到直线l的距离为5,则直线l与⊙O的位置关系是( )
A.相离 B.相切 C.相交 D.无法判断
C
A
2.如图,若⊙的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D,且⊙O的半径为2,则CD的长为( )
A. B. C.2 D. 4
3.如图,PA是⊙O的切线,切点为A,PA= ,
∠APO=30°,则⊙O的半径长为______.
2
4.如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交⊙O于点D.
(1)BD是⊙O的切线吗?为什么?
(2)若AC=10,求线段BC的长度.
解:
(1)BD是⊙O的切线.
证明:∵∠BAD=∠B=30°,
∴∠ADB=180°-30°-30°=120°,∵AO=DO,∴∠A=∠ADO=30°,
∴∠ODB=120°-30°=90°,∴BD是⊙O的切线;
(2)解:∵AC=10,∴CO=5,∴DO=5,∵∠B=30°,∴BO=2DO=10,
在Rt△OBD中:BD= .
第二十四章 圆
24.2.2直线和圆的位置关系(第2课时)
九年级数学上 新课标 [人]
如图所示是一张三角形的铁皮,如何在它的上面剪下一块圆形的用料,并且使圆的面积尽可能的大呢?
1.什么是圆的切线长?
2.过圆外一点可以引圆的几条切线?
3.切线和切线长的区别是什么?
1. 经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长.
如图,过圆外一点P有圆的两条切线PA、PB,则线段PA、PB的长是⊙O的切线长.
2.切线和切线长的区别:
切线是直线,无法度量;
切线长是切线上一条线段的长,
即圆外一点与切点之间的距离,可以度量.
1.在纸上画⊙O,过圆上点A作⊙O的切线PA.
2.连接PO,沿着直线PO将纸对折,设圆上与点A重合的点为点B.
3.连接PB.
1.PB是⊙O的切线吗?
2.图中的PA与PB、∠APO与∠BPO有什么关系?
3.由圆的对称性你能说明你的结论是正确的吗?
4.分析已知和求证,写出逻辑证明过程.
已知:如上图,已知PA、PB是⊙O的两条切线,切点分别为A,B.
求证:PA=PB,∠OPA=∠OPB.
证明:连接OA、OB.
∵PA和PB是⊙O的两条切线,
∴OA⊥AP,OB⊥BP,
又OA=OB,OP=OP,∴Rt△AOP≌Rt△BOP,
∴PA=PB,∠APO=∠BPO.
如图是一块三角形的铁皮,如何在它上面截下一块圆形的用料,并且使截下来的圆与三角形的三条边都相切
A
B
C
1.刚才所画的三角形三条角平分线的交点有什么性质?
2.作圆的关键是什么?
3.如果我们已经作出圆,圆心满足什么条件?
4.找到圆心后,如何确定圆的半径?
内切圆:与三角形各边都相切的圆叫三角形的内切圆.内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
如图所示,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9,BC=14,CA=13.求AF、BD、CE的长.
观察图形和已知,⊙O与BC,CA,AB
分别相切于点D,E,F,,
则根据切线长定理可得 ,
又因为AB=9,BC=14,CA=13,
所以有等量关系 ,
, .
根据等量关系,考虑方程思想解答,所以设 ,根据等量关系可以用未知数表示线段 ,所以可列方程 ,解方程可得.
由BD+CD=BC,可得(13-x)+(9-x)=14.
解:设AF=x,则AE=x,CD=CE=AC-AE=13-x,
BD=BF=AB-AF=9-x.
解得x=4.
因此AF=4,BD=5,CE=9.
1.切线长定义:
经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长.
2.切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
小结
3.三角形的内切圆:
与三角形各边都相切的圆叫三角形的内切圆.内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
小结
1.如图所示,从圆外一点P引⊙O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=10,则弦AB的长( )
A.5 B. C.10 D.
C
C
2.从圆外一点向半径为9的圆作切线,已知切线长为18,从这点到圆的最短距离为( ).
A. B.9( ) C.9( ) D.9
3.如图,PA、PB分别切⊙O于A、B,并与⊙O的切线分别相交于C、D,已知PA=7cm,则△PCD的周长等于_________.
14cm
4.如图,AB,BC,CD分别与⊙O相切于E,F,G.且AB∥CD.BO=6cm,CO=8cm.
求证:BO⊥CO;
证明:∵AB∥CD,∴∠ABC+∠BCD=180°,∵AB、BC、CD分别与⊙O相切于E、F、G,
∴∠OBC= ∠ABC,∠OCB= ∠DCB,
∴∠OBC+∠OCB=(∠ABC+∠DCB)=×180°=90°,∴∠BOC=90°,∴BO⊥CO.
谢 谢 观 看
同课章节目录
