鲁教版(五四制)数学八年级上册5.2.3 平行四边形的判定 课件(共15张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学八年级上册5.2.3 平行四边形的判定 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 10:33:15 | ||
图片预览




文档简介
(共15张PPT)
5.2-3 平行四边形的判定
1.熟记平行四边形的判定定理3,并会进行证明;
2.会在实际问题中灵活应用平行四边形的判定定理进行计算和证明。
学习目标
有一个平行四边形的玻璃,不小心碰碎了一部分,聪明的师傅很快将原来的玻璃复原了出来,你知道他用的是什么方法吗?
情境导入
边
两组对边分别平行
两组对边分别相等
一组对边平行且相等
平行四边形
对角线
?
性质:平行四边形的对角线互相平分
写出它的逆命题:
对角线互相平分的四边形是平行四边形
知识回顾
?
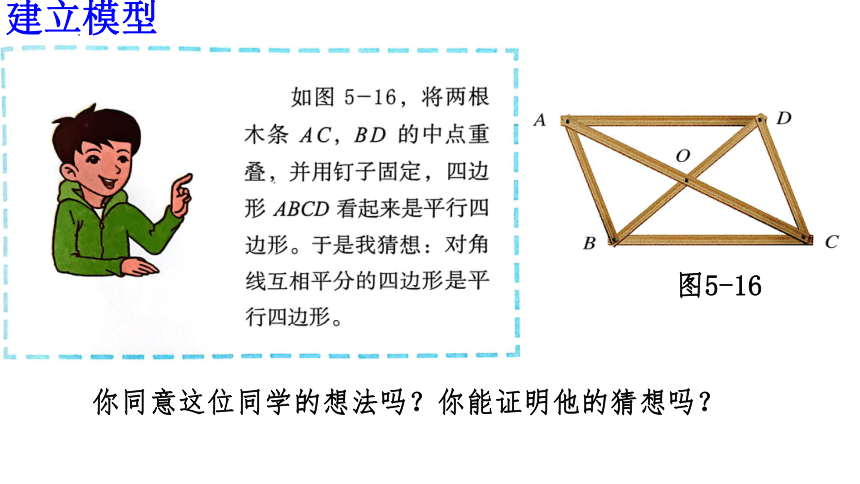
建立模型
你同意这位同学的想法吗?你能证明他的猜想吗?
图5-16
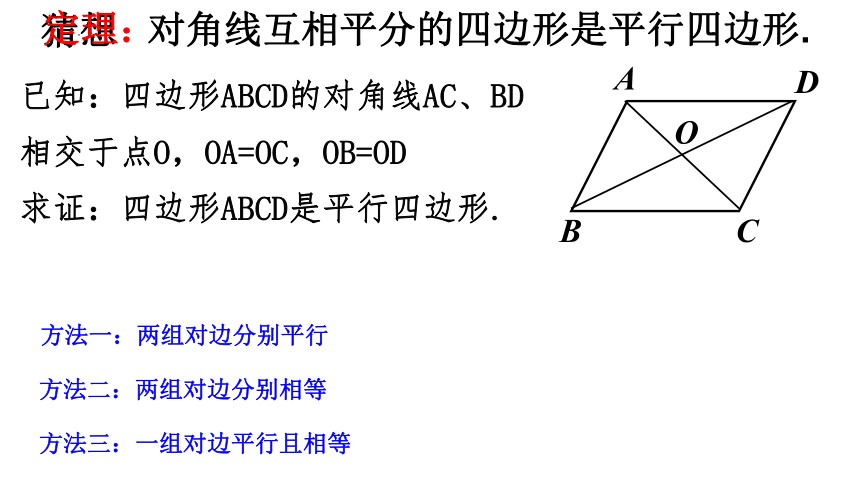
对角线互相平分的四边形是平行四边形.
A
D
C
B
O
已知:四边形ABCD的对角线AC、BD相交于点O,OA=OC,OB=OD
求证:四边形ABCD是平行四边形.
方法一:两组对边分别平行
方法二:两组对边分别相等
方法三:一组对边平行且相等
猜想
定理:
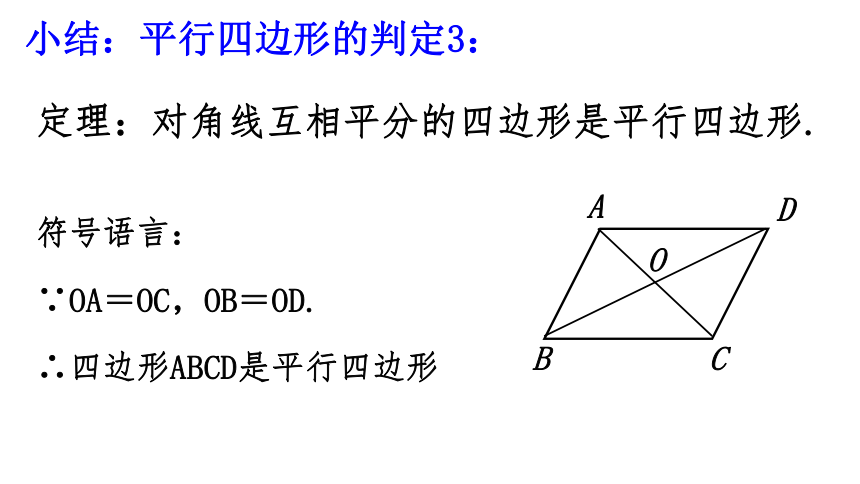
小结:平行四边形的判定3:
定理:对角线互相平分的四边形是平行四边形.
∴四边形ABCD是平行四边形
符号语言:
∵OA=OC,OB=OD.
A
D
C
B
O
知识应用
已知:如图,把△ABC的中线AD延长至E,使得DE=AD,连结EB,EC,求证:四边形ABEC是平行四边形.
E
D
C
B
A
例题解析
例3 已知:如图,E,F我分别是□ABCD的对角线 AC上的两点,且AE=CF .
求证:四边形BFDE是平行四边形.
O
B
A
C
D
E
F
例题变式
1.在□ABCD中,对角线AC与BD相交于点O,E,F分别是OA和OC的中点,四边形BFDE是平行四边形吗?请说明理由.
A
D
B
C
E
F
O
例题变式
A
D
B
C
E
F
O
2. 如图,已知□ABCD 的两条对角线AC与BD相交于点O,E,F是BD上的两点.
(1)当BE,DF满足什么条什时,四边形 AECF是平行四边形?请说明理由;
(2)当∠AEB与∠CFD满足什么条件时,四边形 AECF 是平行四边形?请说明理由.
拓展应用
(教材P136 第4题)
达标练习
1.如下图,在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC= cm,CD= cm时,四边形ABCD为平行四边形;
(2)若AC=10cm,BD=8cm,那么当AO= cm,DO= cm时,四边形ABCD为平行四边形.
2.如下图所示,四边形ABCD的对角线AC和BD相交于点O,下列判断正确的是( ).
A.若AO=OC,则ABCD是平行四边形;
B.若AC=BD,则ABCD是平行四边形;
C.若AO=BO,CO=DO,则ABCD是平行四边形;
D.若AO=OC,BO=OD,则ABCD是平行四边形
达标练习
3.如图,平行四边形ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F.求证:四边形AECF是平行四边形.
达标练习
5.2-3 平行四边形的判定
1.熟记平行四边形的判定定理3,并会进行证明;
2.会在实际问题中灵活应用平行四边形的判定定理进行计算和证明。
学习目标
有一个平行四边形的玻璃,不小心碰碎了一部分,聪明的师傅很快将原来的玻璃复原了出来,你知道他用的是什么方法吗?
情境导入
边
两组对边分别平行
两组对边分别相等
一组对边平行且相等
平行四边形
对角线
?
性质:平行四边形的对角线互相平分
写出它的逆命题:
对角线互相平分的四边形是平行四边形
知识回顾
?
建立模型
你同意这位同学的想法吗?你能证明他的猜想吗?
图5-16
对角线互相平分的四边形是平行四边形.
A
D
C
B
O
已知:四边形ABCD的对角线AC、BD相交于点O,OA=OC,OB=OD
求证:四边形ABCD是平行四边形.
方法一:两组对边分别平行
方法二:两组对边分别相等
方法三:一组对边平行且相等
猜想
定理:
小结:平行四边形的判定3:
定理:对角线互相平分的四边形是平行四边形.
∴四边形ABCD是平行四边形
符号语言:
∵OA=OC,OB=OD.
A
D
C
B
O
知识应用
已知:如图,把△ABC的中线AD延长至E,使得DE=AD,连结EB,EC,求证:四边形ABEC是平行四边形.
E
D
C
B
A
例题解析
例3 已知:如图,E,F我分别是□ABCD的对角线 AC上的两点,且AE=CF .
求证:四边形BFDE是平行四边形.
O
B
A
C
D
E
F
例题变式
1.在□ABCD中,对角线AC与BD相交于点O,E,F分别是OA和OC的中点,四边形BFDE是平行四边形吗?请说明理由.
A
D
B
C
E
F
O
例题变式
A
D
B
C
E
F
O
2. 如图,已知□ABCD 的两条对角线AC与BD相交于点O,E,F是BD上的两点.
(1)当BE,DF满足什么条什时,四边形 AECF是平行四边形?请说明理由;
(2)当∠AEB与∠CFD满足什么条件时,四边形 AECF 是平行四边形?请说明理由.
拓展应用
(教材P136 第4题)
达标练习
1.如下图,在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC= cm,CD= cm时,四边形ABCD为平行四边形;
(2)若AC=10cm,BD=8cm,那么当AO= cm,DO= cm时,四边形ABCD为平行四边形.
2.如下图所示,四边形ABCD的对角线AC和BD相交于点O,下列判断正确的是( ).
A.若AO=OC,则ABCD是平行四边形;
B.若AC=BD,则ABCD是平行四边形;
C.若AO=BO,CO=DO,则ABCD是平行四边形;
D.若AO=OC,BO=OD,则ABCD是平行四边形
达标练习
3.如图,平行四边形ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F.求证:四边形AECF是平行四边形.
达标练习
