第一章 丰富的图形世界 复习课(共22张PPT)2023-2024学年北师大版数学七年级上册
文档属性
| 名称 | 第一章 丰富的图形世界 复习课(共22张PPT)2023-2024学年北师大版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 742.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 10:40:31 | ||
图片预览








文档简介
(共22张PPT)
第一章 丰富的图形世界
第一章 复习课
1.知道正方体、圆柱、圆锥等几何体的侧面展开图,能根据展开图判断和制作简单的立体模型.
2.知道平面截一个几何体的截面是一个平面图形,能判断截面的形状.
3.能识别、能画立方体及简单组合体的从三个不同方向看的形状图.
◎重点:能把简单几何体展开、折叠,会画、会识别从不同方向看几何体的形状图.
◎难点:由从不同方向看几何体的形状图确定几何体的形状.
几何之父——欧几里得经过深入探究,他得出结论:图形是神绘制的,所有一切现象的逻辑规律都体现在图形之中.因此,对智慧训练,就应该从以图形为主要研究对象的几何学开始.今天就让我们通过第一章的复习,踏上智慧训练之旅!
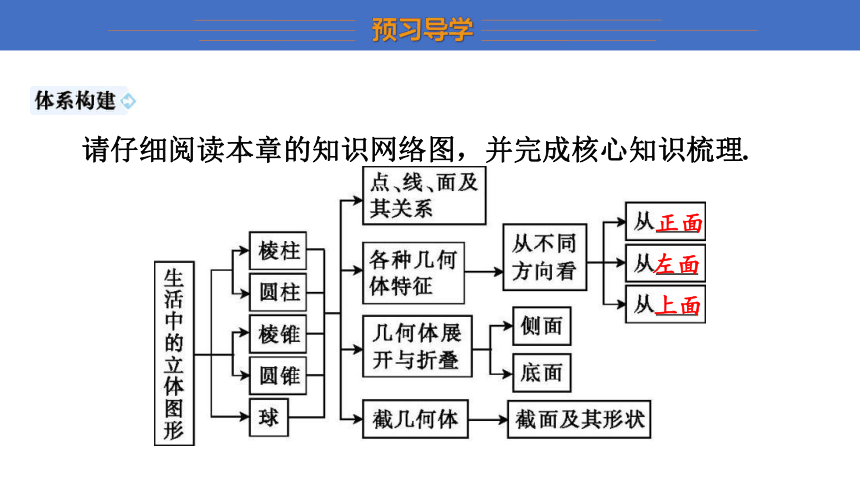
请仔细阅读本章的知识网络图,并完成核心知识梳理.
正面
左面
上面
1.棱柱的上下底面是多边形,它们的形状、大小完全 相同 ,其他各面为棱柱的侧面,且每个侧面都是 平行四边形(或长方形) .棱柱的侧面展开是 平行四边形(或长方形) .
2.棱锥有一个底面,每个侧面都是 三角形 .
3.圆柱的上下两个底面是两个 圆 ,它们半径 相等 ,侧面是由一个 曲 面围成的,侧面展开后是一个 长方形 .
相
同
平行四边形
(或长方形)
平行四边形(或长方形)
三角形
圆
相等
曲
长方形
4.圆锥的底面是 圆 ,侧面是一个 曲 面,侧面展开后是一个 扇形 .
5.球是由 一 个 曲 面围成的.
6.用平面去截一个几何体,截面是一个 平面 图形.
圆
曲
扇形
一
曲
平面
·导学建议·
以问题形式引导学生回顾、归纳本章所学知识,让学生在思考、交流的活动中进一步巩固所学知识.
几何体的展开与折叠
1.李明为好友制作一个正方体礼品盒(如图),六面上各有一字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是 ( C )
C
变式演练 马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如左图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在右图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子(添加所有符合要求的正方形,添加的正方形用阴影表示).
解:本小题的设计比较灵活,答案不唯一.可在上图中标有1、2、3、4的位置上选择接一个正方形,并涂上阴影.
·导学建议·
正方体的展开图形式多样,要注重指导学生分类巧记,在纷繁复杂中寻求规律性,借此培养学生良好的学习习惯.
截一个几何体
2.如图,把一个边长为2 cm的立方体截成八个边长为1 cm的小立方体,至少需截 3 次.
3
3.下列说法正确的是( D )
A.长方体的截面一定是长方形
B.正方体的截面一定是正方形
C.圆锥的截面一定是三角形
D.球体的截面一定是圆
方法归纳交流 一般情况下,用平面去截一个几何体,截面的形状 不唯一 (填“唯一”或“不唯一”),只有球体的截面形状是 唯一 的,从任何角度去截都是 圆 .
D
不唯一
唯一
圆
·导学建议·
同一个几何体有不同的截面形状,同一个截面形状又可能对应多种几何体,“截一个几何体”注重培养学生的空间想象能力和发散思维,在教学时要注重这些方面的引导.
4.如图,这是六个棱长为1的立方块组成的一个几何体,则从上面看该几何体所得形状图的面积是( B )
A.6 B.5 C.4 D.3
B
从三个方向看物体的形状
5.一个几何体由若干大小相同、棱长都为1的小正方体搭成,从正面和左面看这个几何体的形状图如图所示,那么下列选项中一定不是从上面看该几何体所得到的形状图的是( D )
A B C D
D
方法归纳交流 为什么一般情况下会从三个不同的方向看几何体?而不是从两个方向或更多的方向看?
解:一般情况下,从三个方向去看一个几何体,基本上能够确定几何体的形状.如果只从两个方向看的话,往往不能确定其形状.而一.般.的.几何体对面形状相同,所以没有必要从更多的方向去看.
6.如图,这是一个食品包装盒的侧面展开图(底面为正大边形).
(1)这个多面体的形状是 .
(2)请根据图中所标的尺寸,计算这个多面体的侧面积.
解:(1)六棱柱.
综合运用知识
(2)侧面积为6ab.
方法归纳交流 棱柱的侧面展开图是一个 长方形 ,长方形的一边是棱柱的 高 ,另一边是底面多边形的 周长 .
长方形
高
周长
1.要得到正方体的平面展开图需剪开 7 条棱.
2.能否移动右图中一个正方形的位置,使得其折叠后可以得到一个无盖的正方体纸盒?
解:方法多样,仿照四个一排,三个一排,二个一排的方式进行移动就行.
7
解:方法多样,仿照四个一排,三个一排,二个一排的方式
进行移动就行.
·导学建议·
备选问题第1题主要培养学生从反面去思考问题,从而得到解决问题的方法:想要知道剪开多少条棱,就要先知道共有多少条棱,有多少条没有剪开,知道了这两个量之后,自然也就知道了有多少条棱剪开了.第2题方法多样,但每一种方法都是基于四种基本类型,引导学生在纷繁的方法中归类,培养学生的归类意识.
第一章 丰富的图形世界
第一章 复习课
1.知道正方体、圆柱、圆锥等几何体的侧面展开图,能根据展开图判断和制作简单的立体模型.
2.知道平面截一个几何体的截面是一个平面图形,能判断截面的形状.
3.能识别、能画立方体及简单组合体的从三个不同方向看的形状图.
◎重点:能把简单几何体展开、折叠,会画、会识别从不同方向看几何体的形状图.
◎难点:由从不同方向看几何体的形状图确定几何体的形状.
几何之父——欧几里得经过深入探究,他得出结论:图形是神绘制的,所有一切现象的逻辑规律都体现在图形之中.因此,对智慧训练,就应该从以图形为主要研究对象的几何学开始.今天就让我们通过第一章的复习,踏上智慧训练之旅!
请仔细阅读本章的知识网络图,并完成核心知识梳理.
正面
左面
上面
1.棱柱的上下底面是多边形,它们的形状、大小完全 相同 ,其他各面为棱柱的侧面,且每个侧面都是 平行四边形(或长方形) .棱柱的侧面展开是 平行四边形(或长方形) .
2.棱锥有一个底面,每个侧面都是 三角形 .
3.圆柱的上下两个底面是两个 圆 ,它们半径 相等 ,侧面是由一个 曲 面围成的,侧面展开后是一个 长方形 .
相
同
平行四边形
(或长方形)
平行四边形(或长方形)
三角形
圆
相等
曲
长方形
4.圆锥的底面是 圆 ,侧面是一个 曲 面,侧面展开后是一个 扇形 .
5.球是由 一 个 曲 面围成的.
6.用平面去截一个几何体,截面是一个 平面 图形.
圆
曲
扇形
一
曲
平面
·导学建议·
以问题形式引导学生回顾、归纳本章所学知识,让学生在思考、交流的活动中进一步巩固所学知识.
几何体的展开与折叠
1.李明为好友制作一个正方体礼品盒(如图),六面上各有一字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是 ( C )
C
变式演练 马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如左图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在右图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子(添加所有符合要求的正方形,添加的正方形用阴影表示).
解:本小题的设计比较灵活,答案不唯一.可在上图中标有1、2、3、4的位置上选择接一个正方形,并涂上阴影.
·导学建议·
正方体的展开图形式多样,要注重指导学生分类巧记,在纷繁复杂中寻求规律性,借此培养学生良好的学习习惯.
截一个几何体
2.如图,把一个边长为2 cm的立方体截成八个边长为1 cm的小立方体,至少需截 3 次.
3
3.下列说法正确的是( D )
A.长方体的截面一定是长方形
B.正方体的截面一定是正方形
C.圆锥的截面一定是三角形
D.球体的截面一定是圆
方法归纳交流 一般情况下,用平面去截一个几何体,截面的形状 不唯一 (填“唯一”或“不唯一”),只有球体的截面形状是 唯一 的,从任何角度去截都是 圆 .
D
不唯一
唯一
圆
·导学建议·
同一个几何体有不同的截面形状,同一个截面形状又可能对应多种几何体,“截一个几何体”注重培养学生的空间想象能力和发散思维,在教学时要注重这些方面的引导.
4.如图,这是六个棱长为1的立方块组成的一个几何体,则从上面看该几何体所得形状图的面积是( B )
A.6 B.5 C.4 D.3
B
从三个方向看物体的形状
5.一个几何体由若干大小相同、棱长都为1的小正方体搭成,从正面和左面看这个几何体的形状图如图所示,那么下列选项中一定不是从上面看该几何体所得到的形状图的是( D )
A B C D
D
方法归纳交流 为什么一般情况下会从三个不同的方向看几何体?而不是从两个方向或更多的方向看?
解:一般情况下,从三个方向去看一个几何体,基本上能够确定几何体的形状.如果只从两个方向看的话,往往不能确定其形状.而一.般.的.几何体对面形状相同,所以没有必要从更多的方向去看.
6.如图,这是一个食品包装盒的侧面展开图(底面为正大边形).
(1)这个多面体的形状是 .
(2)请根据图中所标的尺寸,计算这个多面体的侧面积.
解:(1)六棱柱.
综合运用知识
(2)侧面积为6ab.
方法归纳交流 棱柱的侧面展开图是一个 长方形 ,长方形的一边是棱柱的 高 ,另一边是底面多边形的 周长 .
长方形
高
周长
1.要得到正方体的平面展开图需剪开 7 条棱.
2.能否移动右图中一个正方形的位置,使得其折叠后可以得到一个无盖的正方体纸盒?
解:方法多样,仿照四个一排,三个一排,二个一排的方式进行移动就行.
7
解:方法多样,仿照四个一排,三个一排,二个一排的方式
进行移动就行.
·导学建议·
备选问题第1题主要培养学生从反面去思考问题,从而得到解决问题的方法:想要知道剪开多少条棱,就要先知道共有多少条棱,有多少条没有剪开,知道了这两个量之后,自然也就知道了有多少条棱剪开了.第2题方法多样,但每一种方法都是基于四种基本类型,引导学生在纷繁的方法中归类,培养学生的归类意识.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
